Como realizar a regressão ols em r (com exemplo)

A regressão de mínimos quadrados ordinários (OLS) é um método que nos permite encontrar uma linha que melhor descreve a relação entre uma ou mais variáveis preditoras e uma variável de resposta .

Este método nos permite encontrar a seguinte equação:

ŷ=b ₀ + b ₁ x

Ouro:

• ŷ : O valor estimado da resposta
• b ₀ : A origem da linha de regressão
• b ₁ : A inclinação da linha de regressão

Esta equação pode nos ajudar a compreender a relação entre o preditor e a variável de resposta e pode ser usada para prever o valor de uma variável de resposta dado o valor da variável preditora.

O exemplo passo a passo a seguir mostra como realizar a regressão OLS em R.

Etapa 1: crie os dados

Para este exemplo, criaremos um conjunto de dados contendo as duas variáveis a seguir para 15 alunos:

• Número total de horas estudadas
• Resultado de exame

Realizaremos uma regressão OLS, usando horas como variável preditora e pontuação no exame como variável resposta.

O código a seguir mostra como criar esse conjunto de dados falso em R:

 #create dataset
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Etapa 2: visualize os dados

Antes de realizar uma regressão OLS, vamos criar um gráfico de dispersão para visualizar a relação entre horas e nota do exame:

 library (ggplot2)

#create scatterplot
ggplot(df, aes(x=hours, y=score)) +
  geom_point(size= 2 )

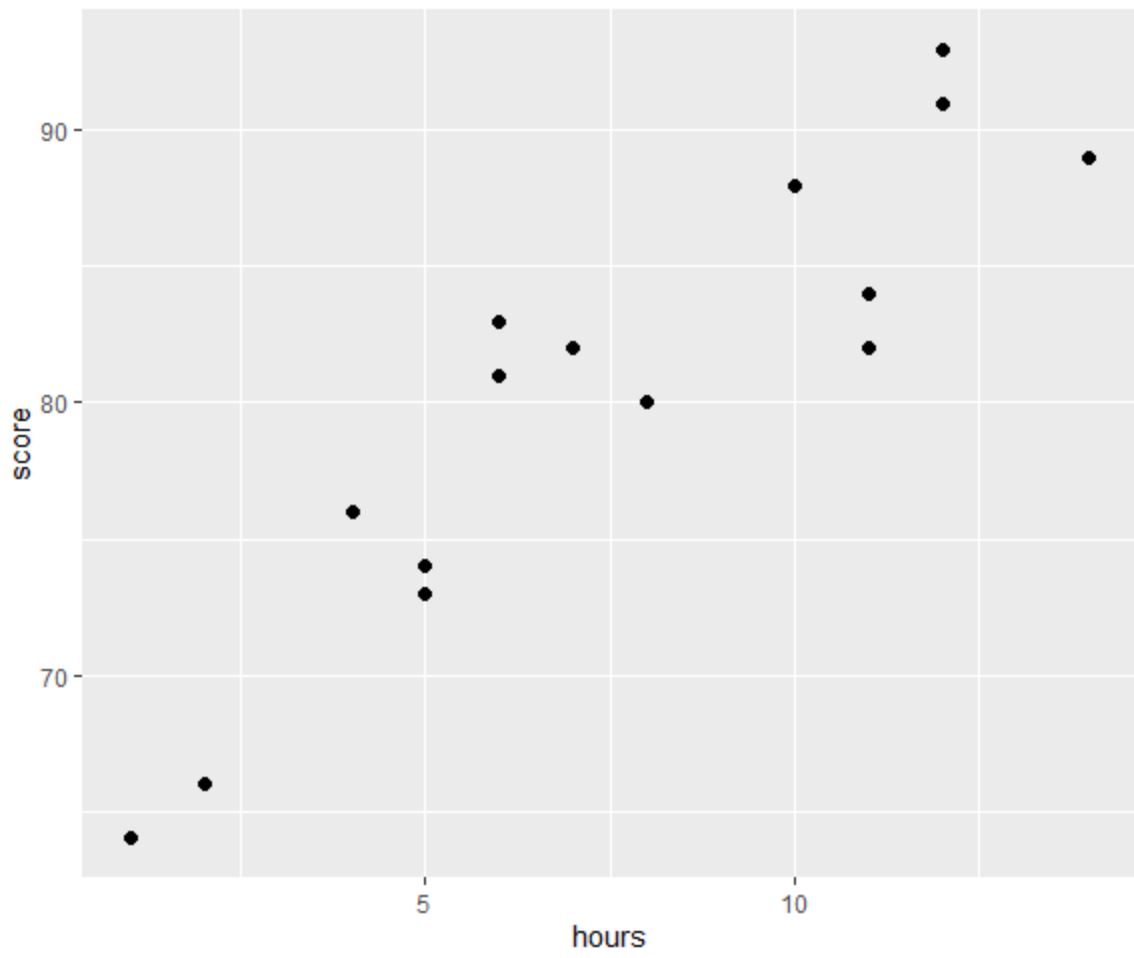
Uma das quatro suposições da regressão linear é que existe uma relação linear entre o preditor e a variável de resposta.

No gráfico podemos ver que a relação parece ser linear. À medida que o número de horas aumenta, a pontuação também tende a aumentar linearmente.

Em seguida, podemos criar um boxplot para visualizar a distribuição dos resultados dos exames e verificar se há outliers.

Nota : R define uma observação como outlier se for 1,5 vezes o intervalo interquartil acima do terceiro quartil ou 1,5 vezes o intervalo interquartil abaixo do primeiro quartil.

Se uma observação for atípica, um pequeno círculo aparecerá no boxplot:

 library (ggplot2)

#create scatterplot
ggplot(df, aes(y=score)) +
  geom_boxplot() 

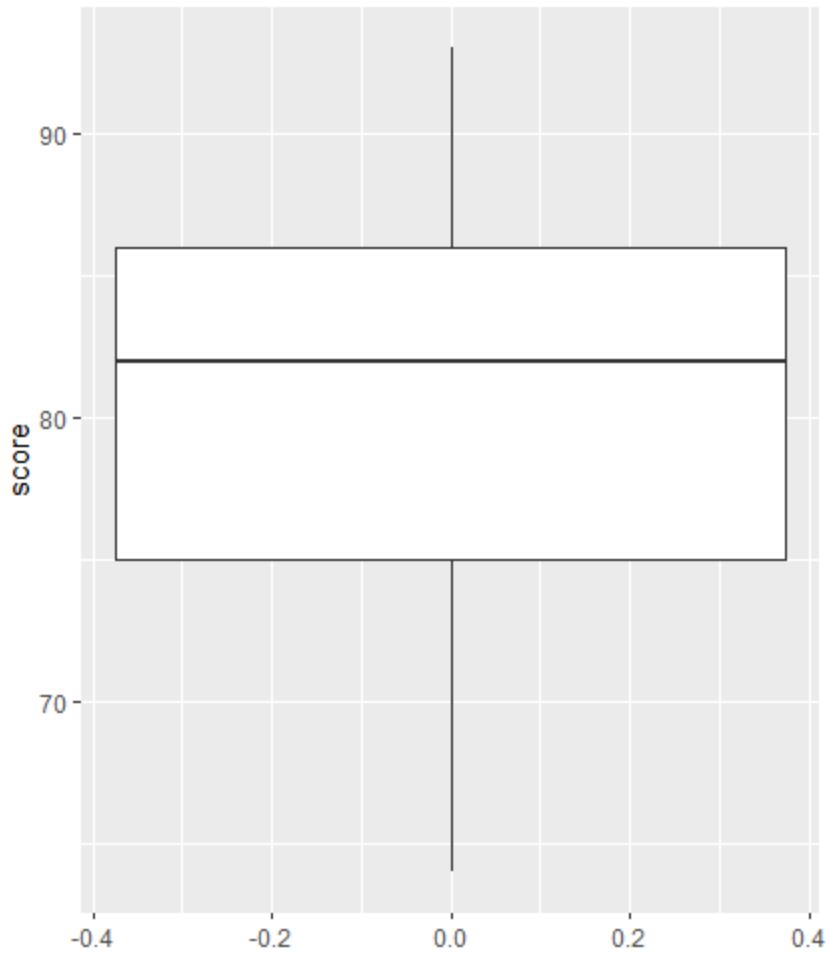
Não há pequenos círculos no boxplot, o que significa que não há valores discrepantes em nosso conjunto de dados.

Etapa 3: realizar a regressão OLS

A seguir, podemos usar a função lm() em R para realizar uma regressão OLS, usando horas como variável preditora e pontuação como variável de resposta:

 #fit simple linear regression model
model <- lm(score~hours, data=df)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

A partir do resumo do modelo, podemos ver que a equação de regressão ajustada é:

Pontuação = 65,334 + 1,982*(horas)

Isso significa que cada hora adicional estudada está associada a um aumento médio na pontuação do exame de 1.982 pontos.

O valor original de 65.334 nos indica a nota média esperada no exame para um aluno que estuda zero horas.

Também podemos usar essa equação para encontrar a pontuação esperada no exame com base no número de horas que um aluno estuda.

Por exemplo, um aluno que estuda 10 horas deverá obter nota 85,15 no exame:

Pontuação = 65,334 + 1,982*(10) = 85,15

Veja como interpretar o restante do resumo do modelo:

• Pr(>|t|): Este é o valor p associado aos coeficientes do modelo. Como o valor p para horas (2,25e-06) é significativamente menor que 0,05, podemos afirmar que existe uma associação estatisticamente significativa entre horas e pontuação .
• Múltiplo R-quadrado: Este número nos diz que a porcentagem de variação nas notas dos exames pode ser explicada pelo número de horas estudadas. Em geral, quanto maior o valor R-quadrado de um modelo de regressão, melhores serão as variáveis preditoras em prever o valor da variável resposta. Nesse caso, 83,1% da variação nas notas pode ser explicada pelas horas estudadas.
• Erro padrão residual: é a distância média entre os valores observados e a linha de regressão. Quanto menor este valor, mais uma linha de regressão é capaz de corresponder aos dados observados. Nesse caso, a pontuação média observada no exame diverge em 3.641 pontos da pontuação prevista pela reta de regressão.
• Estatística F e valor p: A estatística F ( 63,91 ) e o valor p correspondente ( 2.253e-06 ) nos dizem a significância geral do modelo de regressão, ou seja, se as variáveis preditoras no modelo são úteis para explicar a variação . na variável de resposta. Como o valor p neste exemplo é inferior a 0,05, nosso modelo é estatisticamente significativo e as horas são consideradas úteis para explicar a variação da pontuação .

Etapa 4: criar gráficos residuais

Finalmente, precisamos criar gráficos residuais para verificar as suposições de homocedasticidade e normalidade .

A suposição de homocedasticidade é que os resíduos de um modelo de regressão têm variância aproximadamente igual em cada nível de uma variável preditora.

Para verificar se esta suposição é atendida, podemos criar um gráfico de resíduos versus ajustes .

O eixo x exibe os valores ajustados e o eixo y exibe os resíduos. Contanto que os resíduos pareçam estar distribuídos de forma aleatória e uniforme ao longo do gráfico em torno do valor zero, podemos assumir que a homocedasticidade não é violada:

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

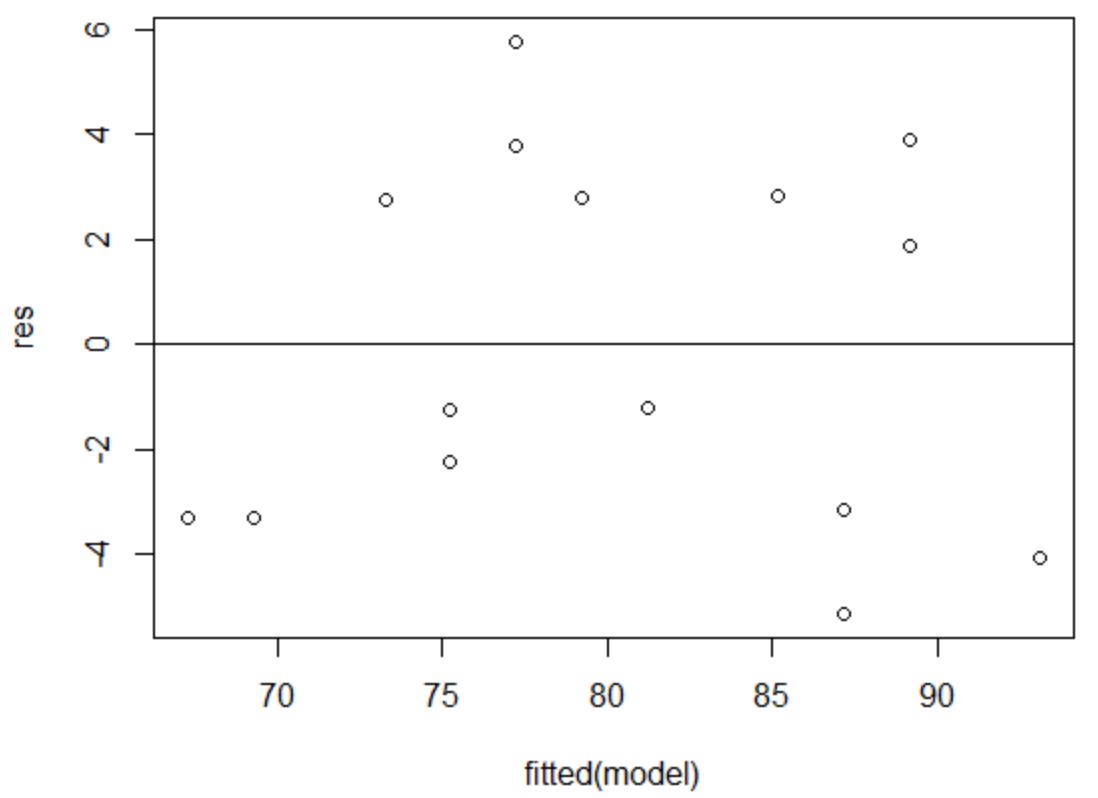
Os resíduos parecem estar espalhados aleatoriamente em torno de zero e não mostram nenhum padrão perceptível, portanto esta suposição é atendida.

A suposição de normalidade afirma que os resíduos de um modelo de regressão são distribuídos aproximadamente normalmente.

Para verificar se esta suposição é atendida, podemos criar um gráfico QQ . Se os pontos do gráfico estiverem ao longo de uma linha aproximadamente reta formando um ângulo de 45 graus, então os dados serão distribuídos normalmente:

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

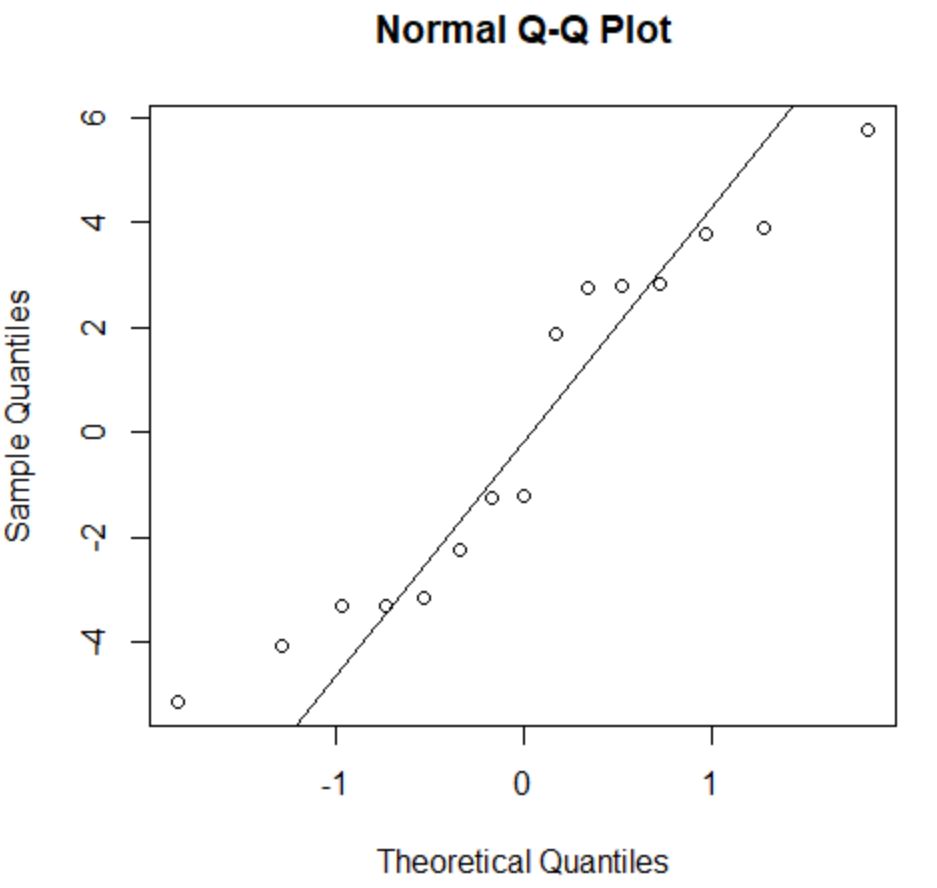
Os resíduos desviam-se um pouco da linha de 45 graus, mas não o suficiente para causar séria preocupação. Podemos assumir que a suposição de normalidade foi atendida.

Como os resíduos são normalmente distribuídos e homocedásticos, verificamos que os pressupostos do modelo de regressão OLS são atendidos.

Assim, a saída do nosso modelo é confiável.

Nota : Se uma ou mais das suposições não fossem atendidas, poderíamos tentar transformar nossos dados.

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras tarefas comuns em R:

Como realizar regressão linear múltipla em R
Como realizar regressão exponencial em R
Como realizar a regressão de mínimos quadrados ponderados em R