A relação entre média e desvio padrão (com exemplo)

A média representa o valor médio em um conjunto de dados.

É calculado da seguinte forma:

Média amostral = Σx _i / n

Ouro:

• Σ: Um símbolo que significa “soma”
• x _i : A i ^-ésima observação em um conjunto de dados
• n: o número total de observações no conjunto de dados

O desvio padrão representa a distribuição dos valores em um conjunto de dados em relação à média.

É calculado da seguinte forma:

Desvio padrão da amostra = √ Σ( _xi – x _barra ) ² / (n-1)

Ouro:

• Σ: Um símbolo que significa “soma”
• x _i : o i- ^ésimo valor da amostra
• x _bar : A amostra significa
• n: O tamanho da amostra

Observe a relação entre a média e o desvio padrão: a média é usada na fórmula para calcular o desvio padrão .

Na verdade, não podemos calcular o desvio padrão de uma amostra a menos que conheçamos a média amostral.

O exemplo a seguir mostra como calcular a média amostral e o desvio padrão amostral para um conjunto de dados na prática.

Exemplo: Calculando a Média e o Desvio Padrão de um Conjunto de Dados

Digamos que temos o seguinte conjunto de dados que mostra os pontos marcados por 10 jogadores de basquete diferentes:

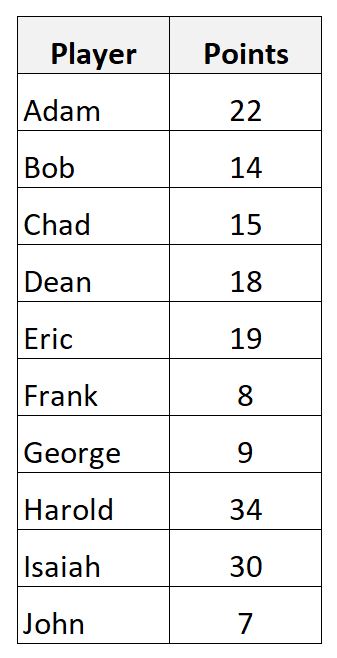Podemos calcular a média amostral de pontos obtidos usando a seguinte fórmula:

• Média amostral = Σx _i / n
• Média amostral = (22+14+15+18+19+8+9+34+30+7) / 10
• Média amostral = 17,6

A média amostral de pontos obtidos é de 17,6 . Isso representa o número médio de pontos marcados entre todos os jogadores.

Depois de sabermos a média amostral, podemos inseri-la na fórmula para calcular o desvio padrão amostral:

• Desvio padrão da amostra = √ Σ(x _i – x _bar ) ² / (n-1)
• Desvio padrão da amostra = √ ((22-17,6) ² + (14-17,6) ² + (15-17,6) ² + (18-17,6) ² + (19-17,6) 6) ² + (8-17,6) ² + (9 -17,6) ² + (34-17,6) ² + (30-17,6) ² + (7-17,6) ² ) / (10-1)
• Desvio padrão amostral = 9,08

O desvio padrão da amostra é 9,08 . Isso representa a distância média entre cada valor de ponto e a média do ponto amostral.

É útil conhecer a média e o desvio padrão de um conjunto de dados porque cada métrica nos diz algo diferente.

A média nos dá uma ideia de onde está o valor “central” de um conjunto de dados.

O desvio padrão nos dá uma ideia da distribuição dos valores em torno da média em um conjunto de dados. Quanto maior o valor do desvio padrão, mais dispersos são os valores em uma amostra.

Conhecendo esses dois valores, podemos aprender muito sobre a distribuição de valores em um conjunto de dados.

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre a média e o desvio padrão:

Por que a média é importante nas estatísticas?
Por que o desvio padrão é importante nas estatísticas?
Como calcular a média e o desvio padrão no Excel