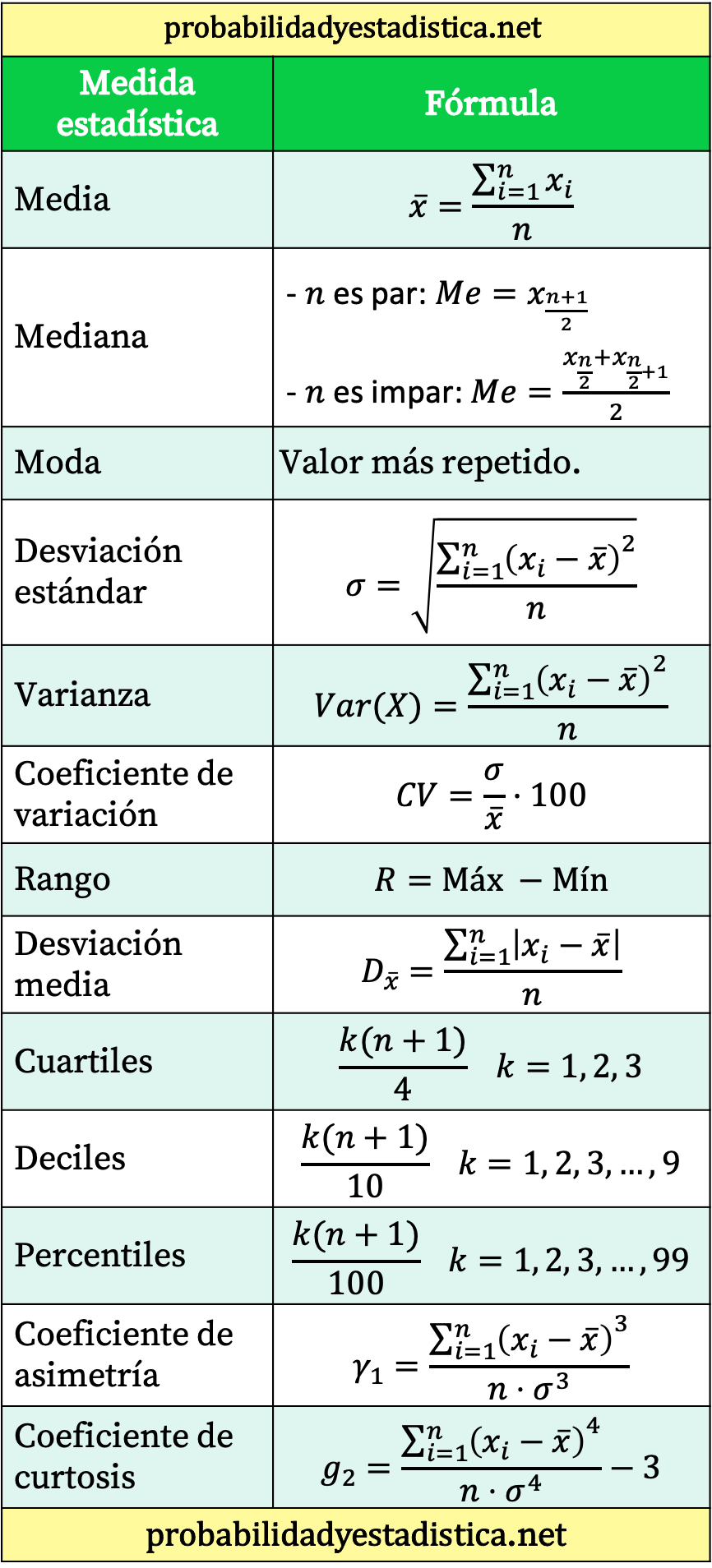
Fórmulas estatísticas
Aqui você encontrará as principais fórmulas estatísticas. Deixamos também um link para nossos artigos nos quais você poderá ver exemplos de aplicação de cada fórmula estatística e, além disso, poderá utilizar uma calculadora online para não ter que fazer os cálculos e saber diretamente o resultado da fórmula.
Fórmulas para medidas estatísticas de tendência central
Metade
Para calcular a média, some todos os valores e depois divida pelo número total de dados. A fórmula para a média é, portanto, a seguinte:
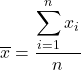
Nas estatísticas, a média também é conhecida como média aritmética ou média .
Mediana
A mediana é o valor médio de todos os dados ordenados do menor para o maior. Em outras palavras, a mediana divide o conjunto de dados ordenado em duas partes iguais.
O cálculo da mediana depende se o número total de dados é par ou ímpar:
- Se o número total de dados for ímpar , a mediana será o valor que fica bem no meio dos dados. Ou seja, o valor que está na posição (n+1)/2 dos dados ordenados.
- Se o número total de pontos de dados for par , a mediana será a média dos dois pontos de dados localizados no centro. Ou seja, a média aritmética dos valores que se encontram nas posições n/2 e n/2+1 dos dados ordenados.
![]()
![]()
Ouro
![]()
é o número total de dados na amostra e o símbolo Me indica a mediana.
Moda
Nas estatísticas, a moda é o valor no conjunto de dados que possui a maior frequência absoluta, ou seja, a moda é o valor mais repetido em um conjunto de dados.
Portanto, não existe uma fórmula específica para a moda, mas para calcular a moda de um conjunto de dados estatísticos, basta contar o número de vezes que cada elemento de dado aparece na amostra, e o dado mais repetido será a moda.
O modo também pode ser considerado modo estatístico ou valor modal .
Fórmulas para medidas estatísticas de dispersão
Desvio padrão
O desvio padrão, também chamado de desvio padrão, é igual à raiz quadrada da soma dos quadrados dos desvios da série de dados dividida pelo número total de observações.
Portanto, a fórmula do desvio padrão é:
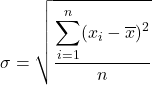
Variância
A variância é igual à soma dos quadrados dos resíduos sobre o número total de observações. A fórmula para esta métrica estatística é, portanto, a seguinte:

Ouro:
-

é a variável aleatória para a qual você deseja calcular a variância.
-

é o valor dos dados

.
-

é o número total de observações.
-

é a média da variável aleatória

.
Coeficiente de variação
Nas estatísticas, o coeficiente de variação é uma medida de dispersão usada para determinar a dispersão de um conjunto de dados em relação à sua média. O coeficiente de variação é calculado dividindo o desvio padrão dos dados pela sua média e depois multiplicando por 100 para expressar o valor em percentagem.
![]()
Limpo
A faixa estatística é uma medida de dispersão que indica a diferença entre o valor máximo e o valor mínimo dos dados em uma amostra. Portanto, para calcular a extensão de uma população ou amostra estatística, o valor máximo deve ser subtraído do valor mínimo.
![]()
Intervalo interquartil
O intervalo interquartil , também chamado de intervalo interquartil , é uma medida de dispersão estatística que indica a diferença entre o terceiro e o primeiro quartis.
Portanto, para calcular o intervalo interquartil de um conjunto de dados estatísticos, você deve primeiro encontrar o terceiro e o primeiro quartil e depois subtraí-los.
![]()
diferença média
O desvio médio , também chamado de desvio médio absoluto , é a média dos desvios absolutos. O desvio médio é, portanto, igual à soma dos desvios de cada item de dados da média aritmética dividida pelo número total de itens de dados.
![]()
Fórmulas para medições estatísticas de posição
quartis
Nas estatísticas, os quartis são os três valores que dividem um conjunto de dados ordenados em quatro partes iguais. Assim, o primeiro, segundo e terceiro quartis representam respectivamente 25%, 50% e 75% de todos os dados estatísticos.
Os quartis são representados por um Q maiúsculo e pelo índice do quartil, portanto o primeiro quartil é Q 1 , o segundo quartil é Q 2 e o terceiro quartil é Q 3 .
A fórmula do quartil é:
![]()
Observação: esta fórmula nos informa a posição do quartil, não o valor do quartil. O quartil serão os dados localizados na posição obtida pela fórmula.
No entanto, por vezes o resultado desta fórmula dá-nos um número decimal. Devemos, portanto, distinguir dois casos dependendo se o resultado é um número decimal ou não:
- Se o resultado da fórmula for um número sem parte decimal , o quartil são os dados que estão na posição fornecida pela fórmula acima.
- Se o resultado da fórmula for um número com parte decimal , o valor do quartil é calculado usando a seguinte fórmula:
![]()
Onde x i e x i+1 são os números das posições entre as quais se localiza o número obtido pela primeira fórmula, ed é a parte decimal do número obtido pela primeira fórmula.
decis
Nas estatísticas, os decis são os nove valores que dividem um conjunto de dados ordenados em dez partes iguais. Para que o primeiro, segundo, terceiro,… decil represente 10%, 20%, 30%,… da amostra ou população.
Os decis são representados pela letra maiúscula D e pelo índice de decil, ou seja, o primeiro decil é D 1 , o segundo decil é D 2 , o terceiro decil é D 3 , etc.
A fórmula do decil é a seguinte:
![]()
Observação: esta fórmula nos informa a posição do decil, não o valor do decil. O decil serão os dados localizados na posição obtida pela fórmula.
Porém, por vezes o resultado desta fórmula nos dará um número decimal, devemos portanto distinguir dois casos dependendo se o resultado é um número decimal ou não:
- Se o resultado da fórmula for um número sem parte decimal , o decil é o dado localizado na posição fornecida pela fórmula acima.
- Se o resultado da fórmula for um número com parte decimal , o valor do decil é calculado usando a seguinte fórmula:
![]()
Onde x i e x i+1 são os números das posições entre as quais se localiza o número obtido pela primeira fórmula, ed é a parte decimal do número obtido pela primeira fórmula.
percentis
Nas estatísticas, os percentis são os valores que dividem um conjunto de dados ordenados em cem partes iguais. Portanto, um percentil indica o valor abaixo do qual cai uma porcentagem do conjunto de dados.
Os percentis são representados pela letra maiúscula P e pelo índice de percentis, ou seja, o primeiro percentil é P 1 , o 40º percentil é P 40 , o 79º percentil é P 79 , etc.
A fórmula do percentil é:
![]()
Atenção: esta fórmula indica-nos a posição do percentil, mas não o seu valor. O percentil serão os dados localizados na posição obtida pela fórmula.
Porém, por vezes o resultado desta fórmula nos dará um número decimal, devemos portanto distinguir dois casos dependendo se o resultado é um número decimal ou não:
- Se o resultado da fórmula for um número sem parte decimal , o percentil corresponde ao dado que está na posição fornecida pela fórmula acima.
- Se o resultado da fórmula for um número com parte decimal , o valor exato do percentil é calculado usando a seguinte fórmula:
![]()
Onde x i e x i+1 são os números das posições entre as quais se localiza o número obtido pela primeira fórmula, ed é a parte decimal do número obtido pela primeira fórmula.
Fórmulas estatísticas de medição de forma
coeficiente de assimetria
O coeficiente de assimetria, ou índice de assimetria, é um coeficiente estatístico usado para determinar a assimetria de uma distribuição. Assim, ao calcular o coeficiente de assimetria, você pode saber o tipo de assimetria da distribuição sem precisar fazer uma representação gráfica dela.
A fórmula para o coeficiente de assimetria é a seguinte:
![]()
Equivalentemente, qualquer uma das duas fórmulas a seguir pode ser usada para calcular o coeficiente de assimetria de Fisher:
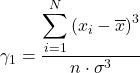
![]()
Ouro
![]()
é a expectativa matemática,
![]()
a média aritmética,
![]()
o desvio padrão e
![]()
o número total de dados.
coeficiente de curtose
A curtose, também chamada de nitidez, indica o quão concentrada uma distribuição está em torno de sua média. Em outras palavras, a curtose indica se uma distribuição é íngreme ou plana. Especificamente, quanto maior a curtose de uma distribuição, mais acentuada (ou mais nítida) ela é.
A fórmula para o coeficiente de curtose é a seguinte:
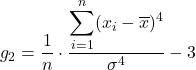
Ouro
![]()
é o valor correspondente à observação
![]()
,
![]()
a média aritmética,
![]()
o desvio padrão e
![]()
o número total de dados.
Tabela resumo de todas as fórmulas estatísticas
Por fim, deixamos uma tabela que resume as principais fórmulas estatísticas.