Como comparar histogramas (com exemplos)

Um histograma é um tipo de gráfico que nos permite visualizar a distribuição dos valores em um conjunto de dados.

O eixo X mostra os valores do conjunto de dados e o eixo Y mostra a frequência de cada valor.

Os histogramas são úteis porque nos permitem compreender rapidamente a distribuição dos valores em um conjunto de dados. Eles também são úteis para comparar dois conjuntos de dados diferentes.

Ao comparar dois ou mais histogramas, podemos responder a três perguntas diferentes:

1. Como os valores medianos se comparam?

Podemos estimar aproximadamente que a mediana está próxima do meio de cada histograma, o que nos permite comparar os valores medianos das distribuições.

2. Como se compara a dispersão?

Podemos ver visualmente qual histograma está mais espalhado, o que nos dá uma ideia de qual distribuição tem valores mais dispersos.

3. Como se compara a assimetria?

Se um histograma tiver uma “cauda” no lado esquerdo do gráfico, ele será assimétrico negativamente. Por outro lado, se um histograma tiver uma “cauda” no lado direito do gráfico, ele será positivamente distorcido. Podemos verificar visualmente cada histograma para comparar a assimetria .

O exemplo a seguir mostra como comparar dois histogramas diferentes e responder a essas três perguntas.

Exemplo: comparando histogramas

Supõe que 200 alunos usem um método de estudo para se preparar para um exame e outros 200 alunos usem um método de estudo diferente para se preparar para o mesmo exame.

Suponha que criemos os seguintes histogramas para comparar os resultados dos exames de cada grupo de alunos:

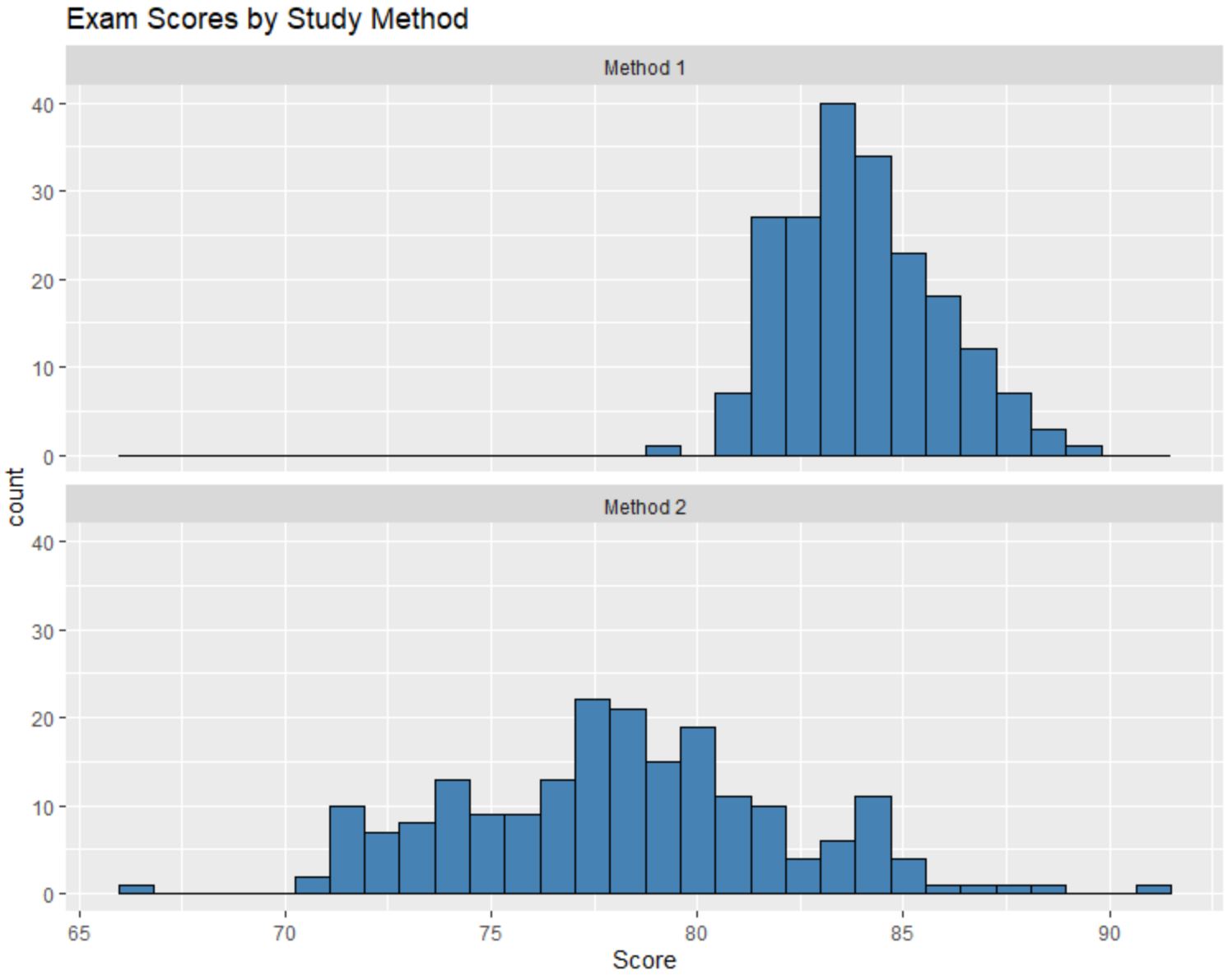
Podemos comparar esses histogramas e responder às três perguntas a seguir:

1. Como os valores medianos se comparam?

Embora não saibamos os valores medianos exatos de cada distribuição simplesmente olhando os histogramas, é óbvio que a nota mediana do exame dos alunos que usaram o Método 1 é maior do que a nota mediana do exame dos alunos que usaram o Método 1. método 2 .

Poderíamos estimar que o valor mediano para o método 1 é em torno de 84 e o valor mediano para o método 2 é em torno de 78.

2. Como se compara a dispersão?

Os valores do histograma do Método 2 são muito mais dispersos do que os do Método 1, o que nos diz que há uma dispersão muito maior nos resultados dos exames para os alunos que utilizaram o Método 2.

3. Como se compara a assimetria?

Olhando para os histogramas, parece que a distribuição das pontuações dos testes para o Método 1 está ligeiramente distorcida para a direita, conforme indicado pela “cauda” que se estende para a direita do histograma.

Contudo, não parece haver uma “cauda” na distribuição dos resultados dos exames para o método 2, o que nos diz que a distribuição é pouco ou nada distorcida.

Bônus : aqui está o código que usamos em R para criar esses dois histogramas:

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras tarefas comuns com histogramas:

Como estimar a média e mediana de qualquer histograma
Como estimar o desvio padrão de qualquer histograma
Como descrever a forma dos histogramas