Como usar o método elbow em r para encontrar clusters ideais
Um dos algoritmos de clustering mais comumente usados em aprendizado de máquina é conhecido como clustering k-means .
O agrupamento K-means é uma técnica na qual colocamos cada observação de um conjunto de dados em um dos K clusters.
O objetivo final é ter K clusters nos quais as observações dentro de cada cluster sejam bastante semelhantes entre si, enquanto as observações em diferentes clusters sejam bastante diferentes umas das outras.
Ao fazer clustering k-means, o primeiro passo é escolher um valor para K – o número de clusters nos quais queremos colocar as observações.
Uma das maneiras mais comuns de escolher um valor para K é conhecida como método do cotovelo , que envolve criar um gráfico com o número de clusters no eixo x e o total na soma dos quadrados no eixo y e, em seguida, identificar onde aparece um “joelho” ou giro na trama.
O ponto no eixo x onde ocorre o “joelho” nos diz o número ideal de clusters a serem usados no algoritmo de agrupamento k-means.
O exemplo a seguir mostra como usar o método cotovelo em R.
Exemplo: Usando o Método Elbow em R
Para este exemplo, usaremos o conjunto de dados USArrests integrado ao R, que contém o número de prisões por 100.000 pessoas em cada estado dos EUA em 1973 por assassinato, agressão e estupro, bem como a porcentagem da população de cada estado vivendo em áreas urbanas. áreas. , UrbanPop.
O código a seguir mostra como carregar o conjunto de dados, remover linhas com valores ausentes e dimensionar cada variável no conjunto de dados para ter uma média de 0 e um desvio padrão de 1:
#load data df <-USArrests #remove rows with missing values df <- na. omitted (df) #scale each variable to have a mean of 0 and sd of 1 df <- scale(df) #view first six rows of dataset head(df) Murder Assault UrbanPop Rape Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473 Alaska 0.50786248 1.1068225 -1.2117642 2.484202941 Arizona 0.07163341 1.4788032 0.9989801 1.042878388 Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602 California 0.27826823 1.2628144 1.7589234 2.067820292 Colorado 0.02571456 0.3988593 0.8608085 1.864967207
Para encontrar o número ideal de clusters para usar no algoritmo k-means, usaremos a função fviz_nbclust() do pacote factoextra para criar um gráfico do número de clusters versus o total na soma dos quadrados:
library (cluster) library (factoextra) #create plot of number of clusters vs total within sum of squares fviz_nbclust(df, kmeans, method = “ wss ”)
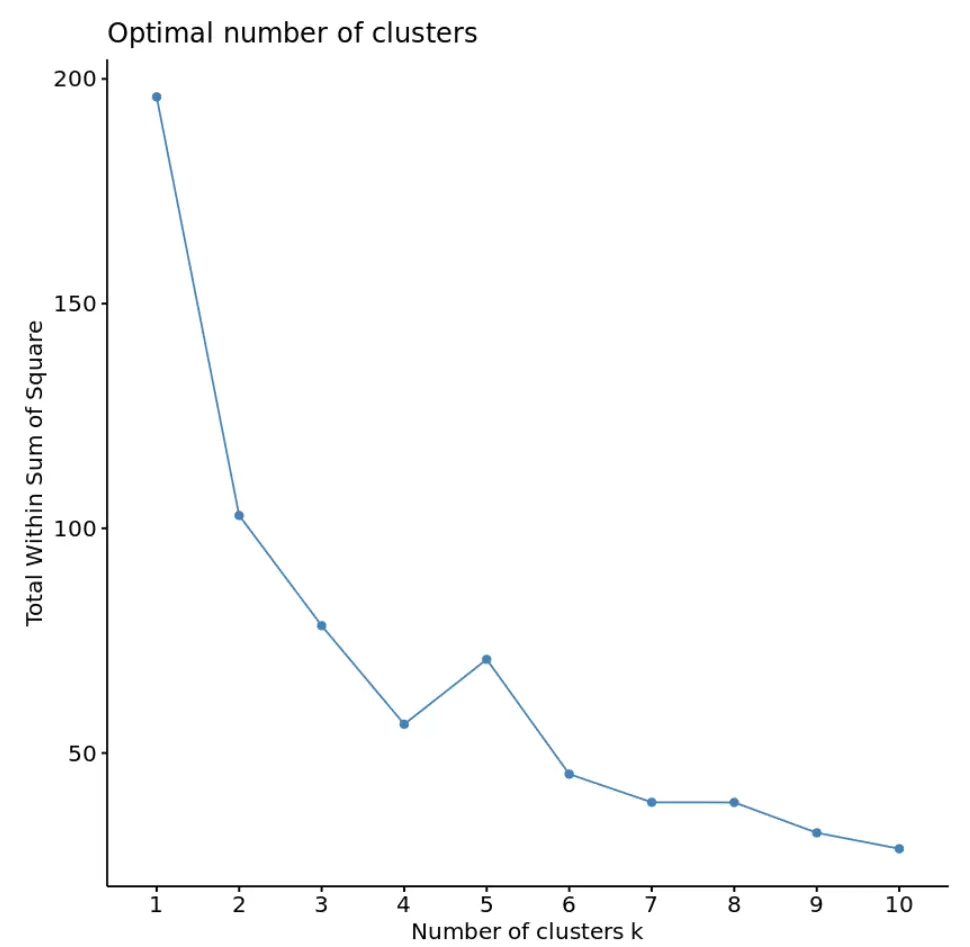
Neste gráfico, parece que há um “joelho” ou torção em k = 4 clusters. Este é o ponto onde o total da soma dos quadrados começa a se estabilizar.
Isso nos diz que o número ideal de clusters a serem usados no algoritmo k-means é 4.
Nota : Embora possamos obter um total menor na soma dos quadrados usando mais clusters, provavelmente superajustaríamos os dados de treinamento e, portanto, o algoritmo k-means não funcionaria tão bem nos dados de teste.
Podemos usar a função kmeans() do pacote cluster para realizar clustering k-means no conjunto de dados usando o valor ideal para k de 4:
#make this example reproducible set. seeds (1) #perform k-means clustering with k = 4 clusters km <- kmeans(df, centers = 4, nstart = 25) #view results km K-means clustering with 4 clusters of sizes 16, 13, 13, 8 Cluster means: Murder Assault UrbanPop Rape 1 -0.4894375 -0.3826001 0.5758298 -0.26165379 2 -0.9615407 -1.1066010 -0.9301069 -0.96676331 3 0.6950701 1.0394414 0.7226370 1.27693964 4 1.4118898 0.8743346 -0.8145211 0.01927104 Vector clustering: Alabama Alaska Arizona Arkansas California Colorado 4 3 3 4 3 3 Connecticut Delaware Florida Georgia Hawaii Idaho 1 1 3 4 1 2 Illinois Indiana Iowa Kansas Kentucky Louisiana 3 1 2 1 2 4 Maine Maryland Massachusetts Michigan Minnesota Mississippi 2 3 1 3 2 4 Missouri Montana Nebraska Nevada New Hampshire New Jersey 3 2 2 3 2 1 New Mexico New York North Carolina North Dakota Ohio Oklahoma 3 3 4 2 1 1 Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 1 1 1 4 2 4 Texas Utah Vermont Virginia Washington West Virginia 3 1 2 1 1 2 Wisconsin Wyoming 2 1 Within cluster sum of squares by cluster: [1] 16.212213 11.952463 19.922437 8.316061 (between_SS / total_SS = 71.2%) Available components: [1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" [7] "size" "iter" "ifault"
Pelos resultados podemos ver que:
- 16 estados foram atribuídos ao primeiro cluster
- 13 estados foram atribuídos ao segundo cluster
- 13 estados foram atribuídos ao terceiro cluster
- 8 estados foram atribuídos ao quarto cluster
Também podemos adicionar as atribuições de cluster de cada estado ao conjunto de dados original:
#add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)
#view final data
head(final_data)
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2
Cada observação do banco de dados original foi colocada em um dos quatro grupos.
Recursos adicionais
Os tutoriais a seguir fornecem exemplos passo a passo sobre como executar vários algoritmos de cluster em R:
Clustering K-Means em R: exemplo passo a passo
Clustering K-Medoids em R: exemplo passo a passo
Clustering hierárquico em R: exemplo passo a passo