Cartão de controle u

Neste artigo explicamos o que é uma placa de controle U, quais são suas características e para que serve. Além disso, você poderá ver como é feito um gráfico de controle U e um exercício resolvido passo a passo.

O que é um cartão de controle U?

Um gráfico de controle U , ou simplesmente gráfico U , é um gráfico que representa o número de vezes que um fenômeno ocorre por unidade de medida quando esta é variável.

Por exemplo, um gráfico de controle U pode ser usado para controlar o número de defeitos por metro quadrado de tecido. Muitas vezes, as amostras de tecido não podem ser coletadas com a mesma área de superfície, portanto, cada amostra é diferente. Assim, a carta U permite estudar processos que possuem tamanho amostral variável.

É importante observar que a carta de controle U não representa o número de unidades defeituosas, mas sim a quantidade de defeitos que cada unidade possui, como na carta C. Em contraste, um gráfico de controle P ou NP controla a proporção e o número de produtos defeituosos. Abaixo veremos as diferenças entre todos os tipos de gráficos de controle.

Tenha em mente que o modelo matemático de referência do gráfico de controle U é a distribuição de Poisson, pois estudamos o número de ocorrências de um fenômeno por unidade de medida.

Como criar um gráfico de controle U

Agora que conhecemos a definição do gráfico de controle U, vamos ver como é feito esse tipo de gráfico de controle:

1. Coleta de amostras : em primeiro lugar, devem ser coletadas diferentes amostras para ver a evolução do fenômeno a ser medido. As amostras devem ser do mesmo tamanho, além disso, recomenda-se colher no mínimo 20 amostras.
2. Determine o número de vezes que o fenômeno ocorre por unidade de medida : para cada amostra, o número de vezes que o fenômeno a ser estudado se repete.
3. Calcular o valor médio das ocorrências : a partir dos dados coletados, é necessário calcular a média das vezes que o fenômeno ocorre por unidade de medida.



4. Calcular os limites de controle do U-Card – Os limites de controle do U-Card devem então ser calculados usando as fórmulas fornecidas abaixo. Tenha em mente que o valor dos limites de controle varia dependendo do tamanho da amostra.





Ouro



E



são respectivamente os limites de controle superior e inferior da amostra i,



é o valor médio das ocorrências e



é o tamanho da amostra i.

5. Plotando valores no mapa – Os valores coletados juntamente com os limites de controle calculados devem agora ser plotados em um mapa para criar o gráfico de controle U.
6. Analise o cartão de controle U : em última análise, tudo o que resta é verificar se nenhum valor no cartão sai dos limites de controle e, portanto, se o processo está sob controle. Caso contrário, devem ser tomadas medidas para corrigir o processo.

Exemplo de cartão de controle U

• Uma empresa industrial deseja controlar o número de defeitos por ^m2 de tecido. A tabela a seguir apresenta as amostras analisadas e o número de defeitos encontrados. Crie um gráfico de controle U para estudar o número de defeitos.

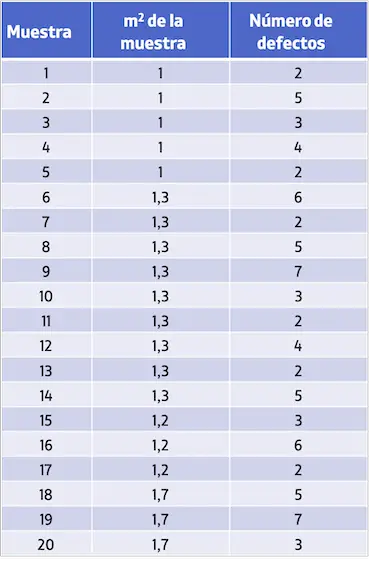
Para criar o gráfico de controle U, primeiro você deve calcular o valor médio do número de defeitos por amostra:

Agora precisamos calcular os limites de controle para cada amostra. A título de exemplo, os limites de controle para a primeira amostra são calculados abaixo:

Todos os limites inferiores de controle resultam em um número negativo, o que não faz sentido. Portanto, definiremos os limites inferiores de controle como 0.

Assim, os valores dos limites de controle para cada amostra são os seguintes:

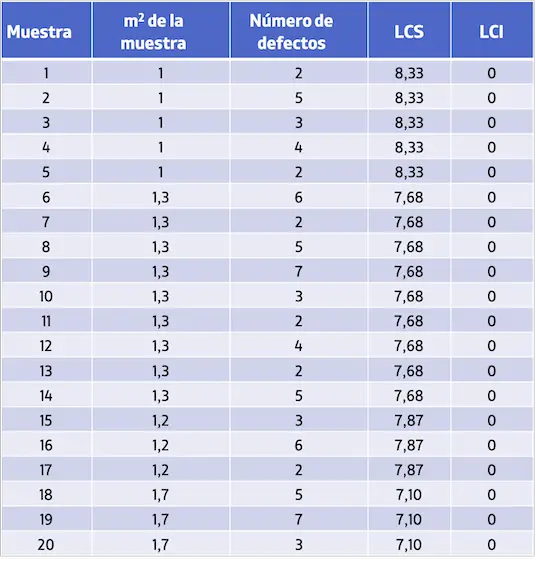
Por fim, basta representar todos os valores em um gráfico para obter o gráfico de controle U:

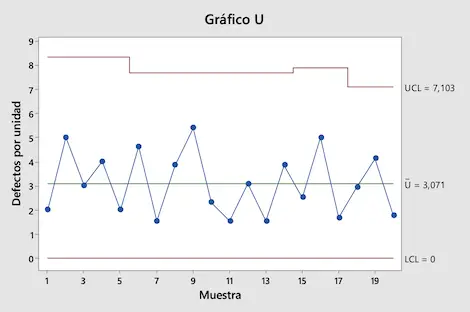
Como você pode ver no gráfico U que fizemos, todos os valores estão entre os limites de controle. Podemos, portanto, concluir que o processo de produção está sob controle.

Outros tipos de gráficos de controle

Além da carta U, existem outros tipos de cartas de controle de atributos:

• Cartão de controle P : a proporção de produtos defeituosos é controlada.
• Cartão de controle NP : o número de produtos defeituosos é controlado.
• Gráfico de controle C : O número de defeitos é controlado como no gráfico U, mas o tamanho da amostra é constante.