Como interpretar um gráfico residual curvo (com exemplo)

Os gráficos de resíduos são usados para avaliar se os resíduos de um modelo de regressão são normalmente distribuídos e se apresentam ou não heterocedasticidade .

Idealmente, você gostaria que os pontos em um gráfico residual fossem espalhados aleatoriamente em torno de um valor zero, sem um padrão claro.

Se você encontrar um gráfico residual no qual os pontos do gráfico possuem um padrão curvo, isso provavelmente significa que o modelo de regressão especificado para os dados não está correto.

Na maioria dos casos, isso significa que você tentou ajustar um modelo de regressão linear a um conjunto de dados que segue uma tendência quadrática.

O exemplo a seguir mostra como interpretar (e corrigir) um gráfico residual curvo na prática.

Exemplo: Interpretando um gráfico residual curvo

Suponha que coletamos os seguintes dados sobre o número de horas trabalhadas por semana e o nível de felicidade relatado (em uma escala de 0 a 100) para 11 pessoas diferentes em um escritório:

Se criássemos um gráfico de dispersão simples de horas trabalhadas versus nível de felicidade, seria assim:

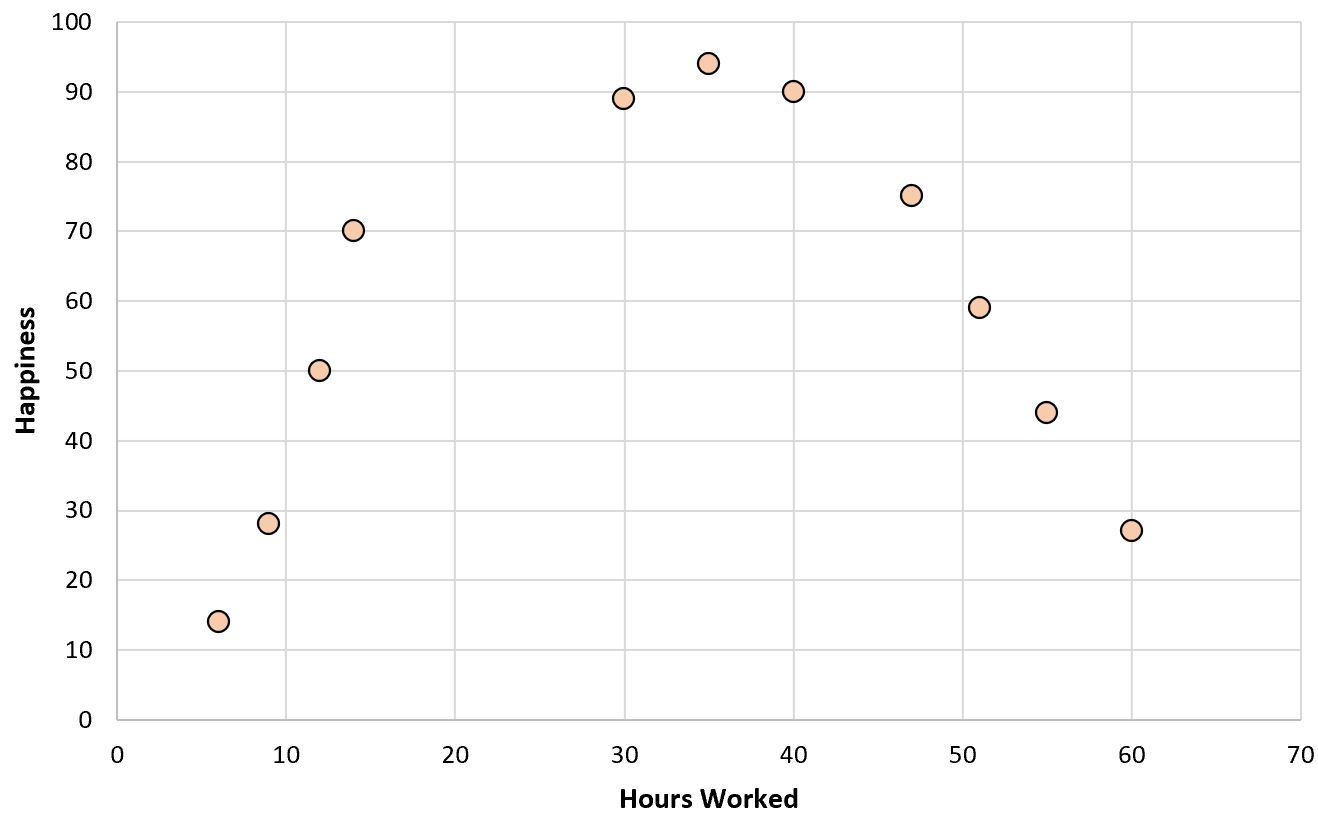
Agora, suponha que queiramos ajustar um modelo de regressão usando horas trabalhadas para prever os níveis de felicidade.

O código a seguir mostra como ajustar um modelo de regressão linear simples a este conjunto de dados e produzir um gráfico residual em R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

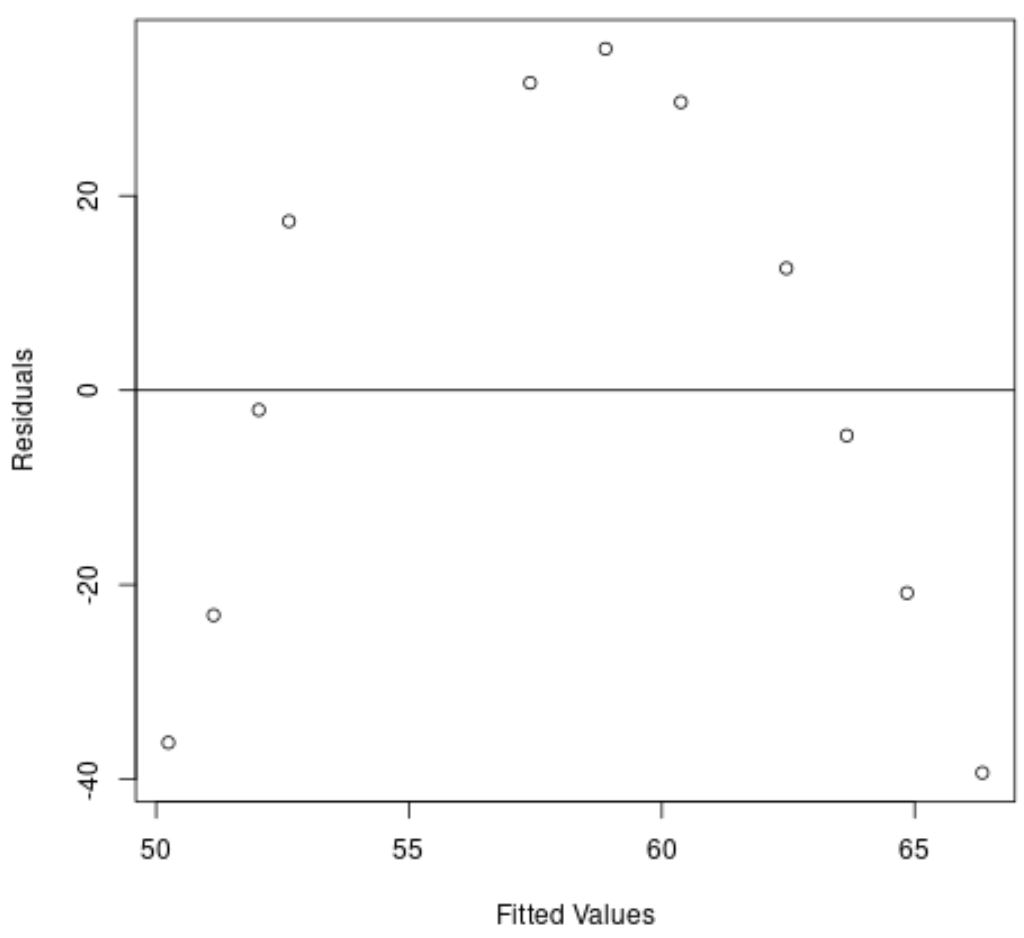
O eixo x exibe os valores ajustados e o eixo y exibe os resíduos.

No gráfico, podemos observar que existe um padrão curvo nos resíduos, indicando que um modelo de regressão linear não fornece um ajuste adequado a este conjunto de dados.

O código a seguir mostra como ajustar um modelo de regressão quadrática a este conjunto de dados e produzir um gráfico residual em R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

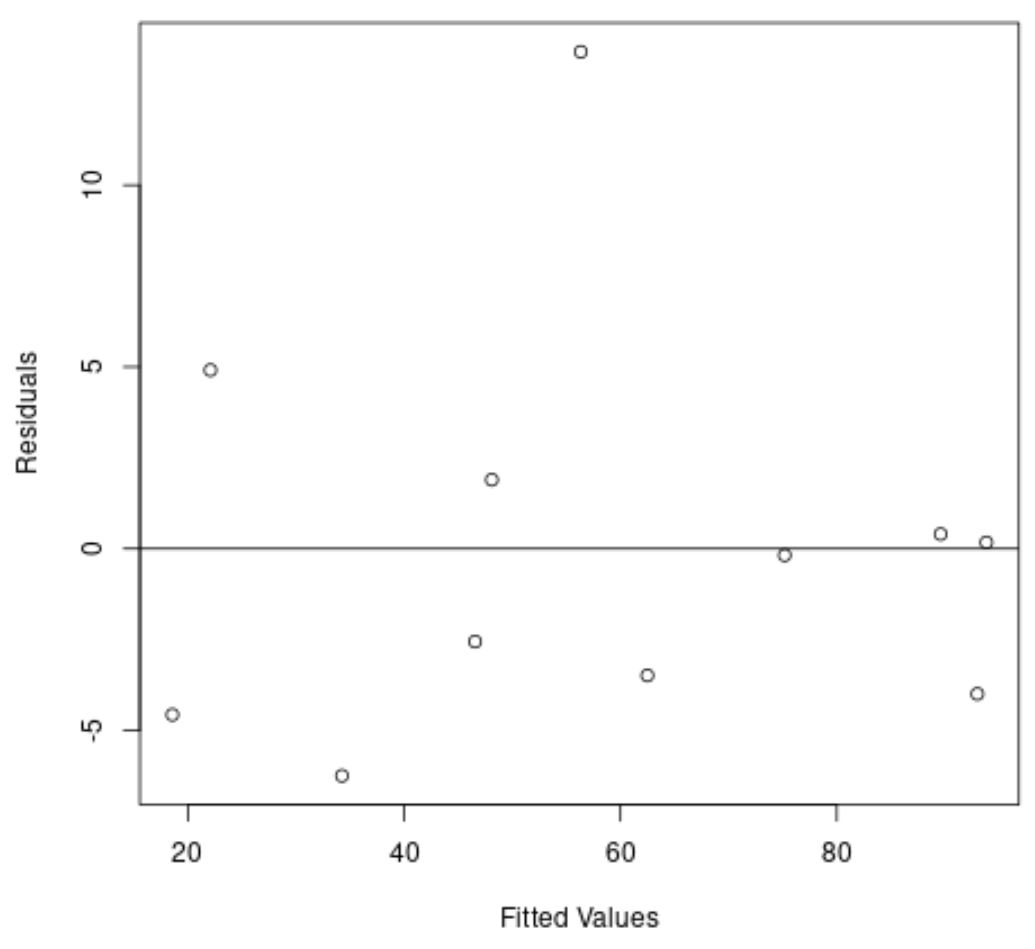
Mais uma vez, o eixo x mostra os valores ajustados e o eixo y mostra os resíduos.

No gráfico podemos ver que os resíduos estão espalhados aleatoriamente em torno de zero e não há uma tendência clara nos resíduos.

Isso nos diz que um modelo de regressão quadrática faz um trabalho muito melhor no ajuste desse conjunto de dados do que um modelo de regressão linear.

Isto deveria fazer sentido, uma vez que vimos que a verdadeira relação entre as horas trabalhadas e os níveis de felicidade parecia ser quadrática e não linear.

Recursos adicionais

Os tutoriais a seguir explicam como criar gráficos residuais usando diferentes softwares estatísticos:

Como criar um caminho residual manualmente
Como criar um gráfico residual em R
Como criar um gráfico residual no Excel
Como criar um gráfico residual em Python