Como realizar um teste cramer-von mises em r (com exemplos)
O teste Cramer-Von Mises é usado para determinar se uma amostra vem ou não de uma distribuição normal .
Este tipo de teste é útil para determinar se um determinado conjunto de dados vem ou não de uma distribuição normal, que é uma suposição comumente usada em muitos testes estatísticos, incluindo regressão , ANOVA , testes t e muitos outros. ‘outros.
Podemos facilmente realizar um teste de Cramer-Von Mises usando a função cvm.test() do pacote goftest em R.
O exemplo a seguir mostra como usar esta função na prática.
Exemplo 1: teste de Cramer-Von Mises em dados normais
O código a seguir mostra como realizar um teste de Cramer-Von Mises em um conjunto de dados com tamanho de amostra n=100:
library (goftest) #make this example reproducible set. seeds (0) #create dataset of 100 random values generated from a normal distribution data <- rnorm(100) #perform Cramer-Von Mises test for normality cvm. test (data, ' pnorm ') Cramer-von Mises test of goodness-of-fit Null hypothesis: Normal distribution Parameters assumed to be fixed data:data omega2 = 0.078666, p-value = 0.7007
O valor p do teste é 0,7007 .
Como este valor não é inferior a 0,05, podemos assumir que os dados amostrais provêm de uma população normalmente distribuída.
Este resultado não deve ser surpreendente, uma vez que geramos os dados amostrais usando a função rnorm() , que gera valores aleatórios a partir de uma distribuição normal padrão .
Relacionado: Um guia para dnorm, pnorm, qnorm e rnorm em R
Também podemos produzir um histograma para verificar visualmente se os dados da amostra estão normalmente distribuídos:
hist(data, col=' steelblue ')
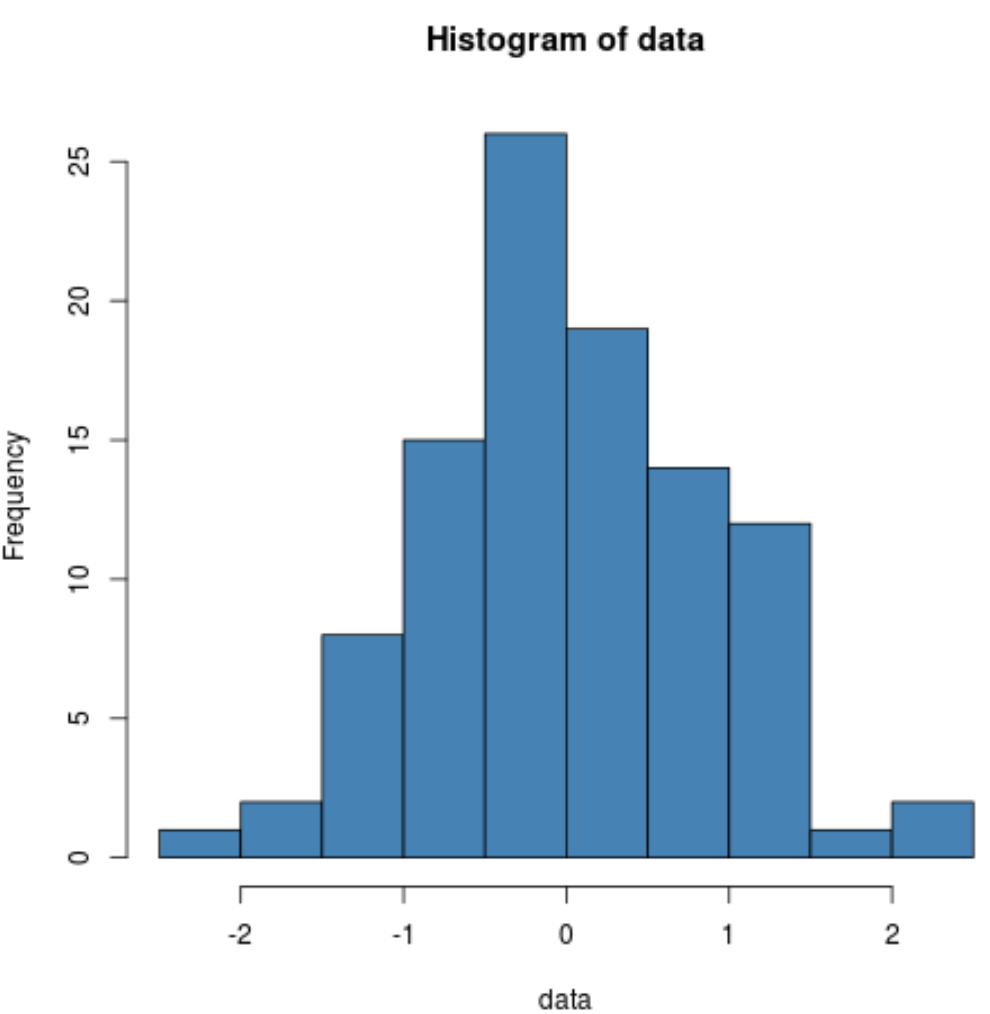
Podemos ver que a distribuição tem formato de sino com um pico no centro da distribuição, o que é típico de dados normalmente distribuídos.
Exemplo 2: Teste Cramer-Von Mises em dados não normais
O código a seguir mostra como realizar um teste de Cramer-Von Mises em um conjunto de dados com tamanho amostral de 100 em que os valores são gerados aleatoriamente a partir de uma distribuição de Poisson :
library (goftest) #make this example reproducible set. seeds (0) #create dataset of 100 random values generated from a Poisson distribution data <- rpois(n=100, lambda=3) #perform Cramer-Von Mises test for normality cvm. test (data, ' pnorm ') Cramer-von Mises test of goodness-of-fit Null hypothesis: Normal distribution Parameters assumed to be fixed data:data omega2 = 27.96, p-value < 2.2e-16
O valor p do teste revelou-se extremamente baixo.
Como este valor é inferior a 0,05, temos evidências suficientes para dizer que os dados amostrais não provêm de uma população normalmente distribuída.
Este resultado não deve ser surpreendente, uma vez que geramos os dados amostrais usando a função rpois() , que gera valores aleatórios a partir de uma distribuição de Poisson.
Relacionado: Um guia para dpois, ppois, qpois e rpois em R
Também podemos produzir um histograma para ver visualmente que os dados da amostra não estão normalmente distribuídos:
hist(data, col=' coral2 ')
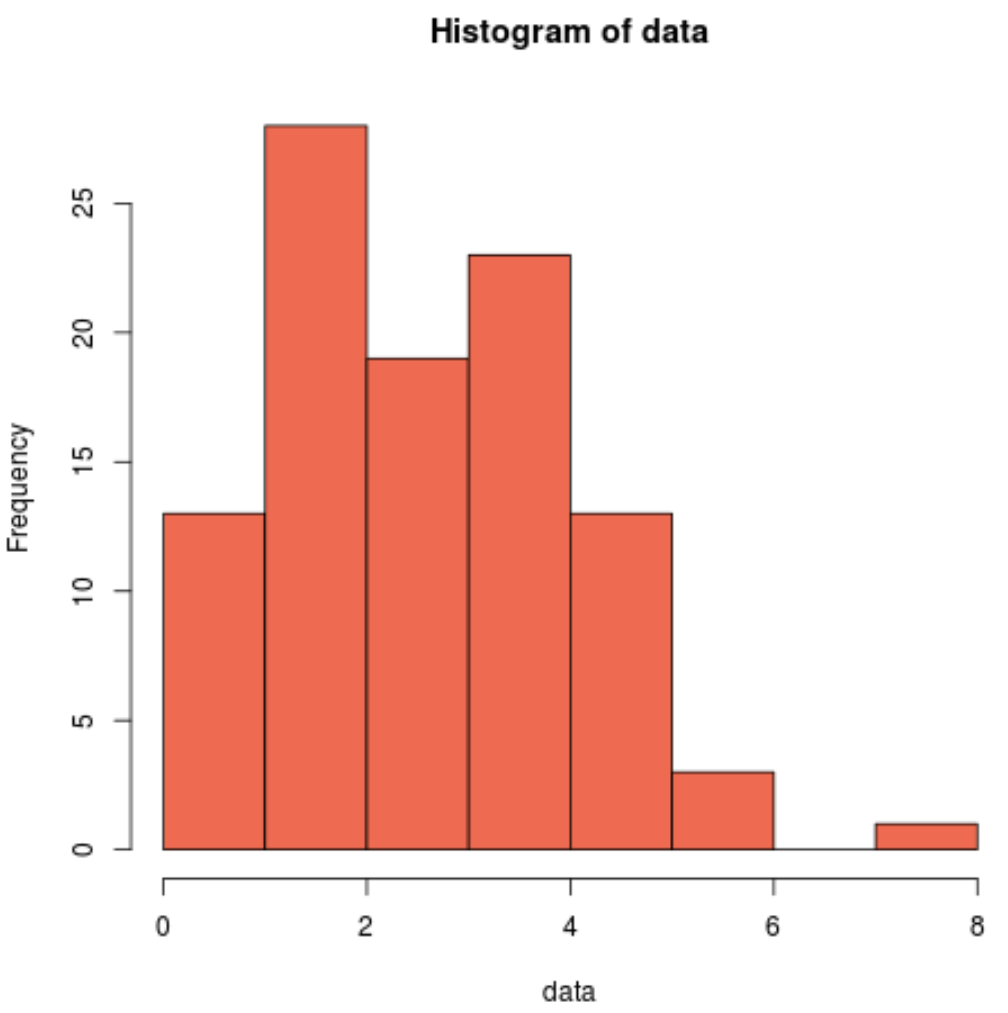
Podemos ver que a distribuição é assimétrica à direita e não possui o típico “formato de sino” associado a uma distribuição normal.
Assim, nosso histograma corresponde aos resultados do teste Cramer-Von Mises e confirma que nossos dados amostrais não provêm de uma distribuição normal.
O que fazer com dados não normais
Se um determinado conjunto de dados não for distribuído normalmente, muitas vezes podemos realizar uma das seguintes transformações para torná-lo mais normal:
1. Transformação de log: transforme a variável de resposta de y em log(y) .
2. Transformação de raiz quadrada: Transforme a variável de resposta de y em √y .
3. Transformação da raiz cúbica: transforme a variável de resposta de y em y 1/3 .
Ao realizar essas transformações, a variável resposta geralmente se aproxima da distribuição normal.
Consulte este tutorial para ver como realizar essas transformações na prática.
Recursos adicionais
Os tutoriais a seguir explicam como realizar outros testes de normalidade em R:
Como realizar um teste de Shapiro-Wilk em R
Como realizar um teste de Anderson-Darling em R
Como realizar um teste de Kolmogorov-Smirnov em R