Como realizar a regressão spline em r (com exemplo)
A regressão spline é um tipo de regressão usada quando há pontos ou “nós” onde o padrão nos dados muda abruptamente e a regressão linear e a regressão polinomial não são flexíveis o suficiente para ajustar os dados.
O exemplo passo a passo a seguir mostra como realizar a regressão spline em R.
Etapa 1: crie os dados
Primeiro, vamos criar um conjunto de dados em R com duas variáveis e criar um gráfico de dispersão para visualizar a relação entre as variáveis:
#create data frame df <- data. frame (x=1:20, y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10, 11, 14, 15, 15, 16, 15, 17, 19, 18, 20)) #view head of data frame head(df) xy 1 1 2 2 2 4 3 3 7 4 4 9 5 5 13 6 6 15 #create scatterplot plot(df$x, df$y, cex= 1.5 , pch= 19 )
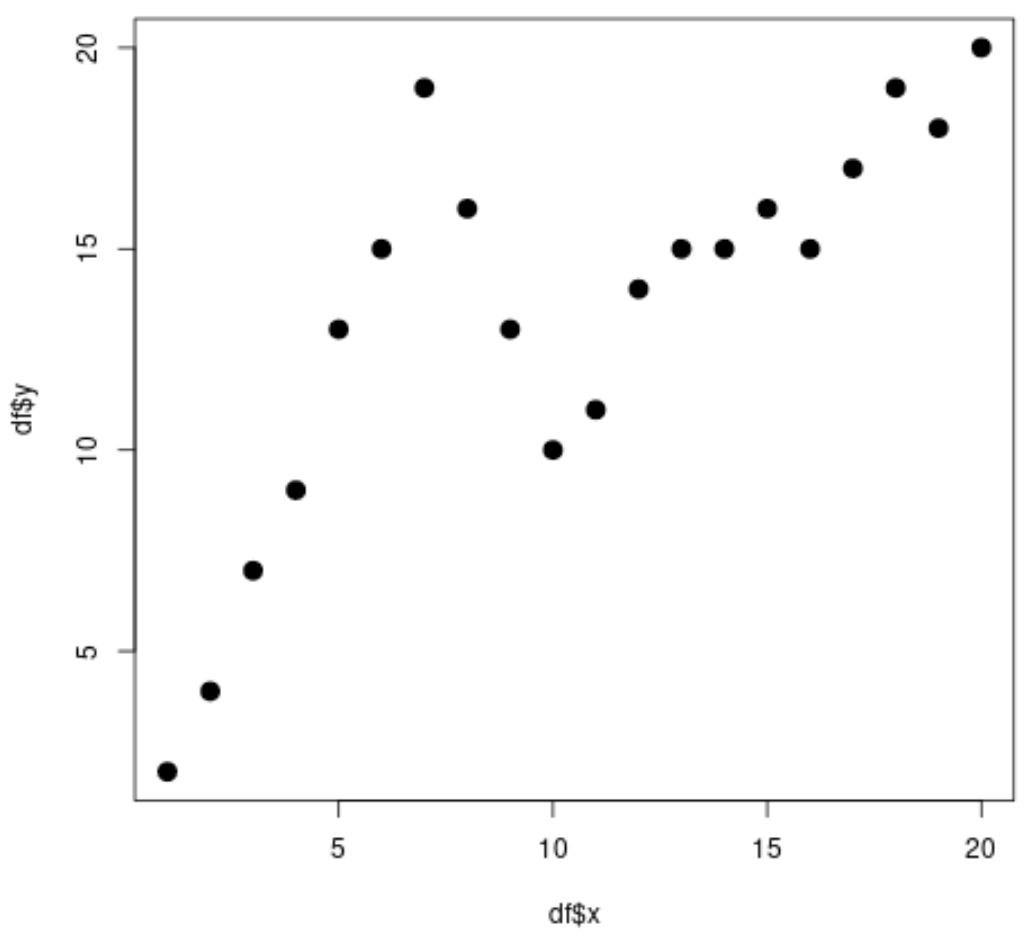
Obviamente, a relação entre x e y não é linear e parece haver dois pontos ou “nós” onde o padrão nos dados muda abruptamente em x=7 e x=10.
Etapa 2: Ajustar o modelo de regressão linear simples
Vamos então usar a função lm() para ajustar um modelo de regressão linear simples a este conjunto de dados e traçar a linha de regressão ajustada no gráfico de dispersão:
#fit simple linear regression model linear_fit <- lm(df$y ~ df$x) #view model summary summary(linear_fit) Call: lm(formula = df$y ~ df$x) Residuals: Min 1Q Median 3Q Max -5.2143 -1.6327 -0.3534 0.6117 7.8789 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 6.5632 1.4643 4.482 0.000288 *** df$x 0.6511 0.1222 5.327 4.6e-05 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.152 on 18 degrees of freedom Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05 #create scatterplot plot(df$x, df$y, cex= 1.5 , pch= 19 ) #add regression line to scatterplot abline(linear_fit)
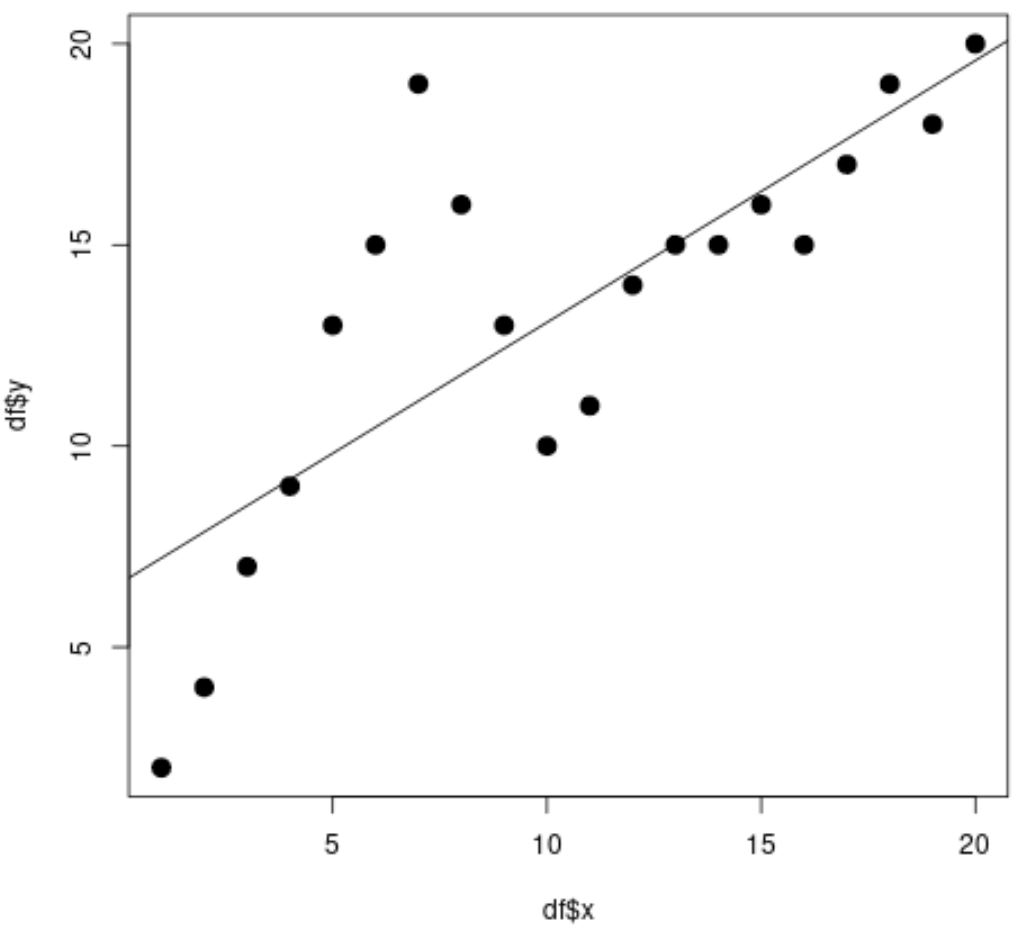
No gráfico de dispersão, podemos ver que a linha de regressão linear simples não se ajusta bem aos dados.
A partir dos resultados do modelo, também podemos ver que o valor R-quadrado ajustado é 0,5903 .
Compararemos isso com o valor R-quadrado ajustado de um modelo spline.
Etapa 3: ajustar o modelo de regressão spline
A seguir, vamos usar a função bs() do pacote splines para ajustar um modelo de regressão spline com dois nós e, em seguida, traçar o modelo ajustado no gráfico de dispersão:
library (splines) #fit spline regression model spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 ))) #view summary of spline regression model summary(spline_fit) Call: lm(formula = df$y ~ bs(df$x, knots = c(7, 10))) Residuals: Min 1Q Median 3Q Max -2.84883 -0.94928 0.08675 0.78069 2.61073 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.073 1.451 1.429 0.175 bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514 bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 *** bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274 bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 *** bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 1.568 on 14 degrees of freedom Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07 #calculate predictions using spline regression model x_lim <- range(df$x) x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ]) preds <- predict(spline_fit, newdata=list(x=x_grid)) #create scatter plot with spline regression predictions plot(df$x, df$y, cex= 1.5 , pch= 19 ) lines(x_grid, preds)
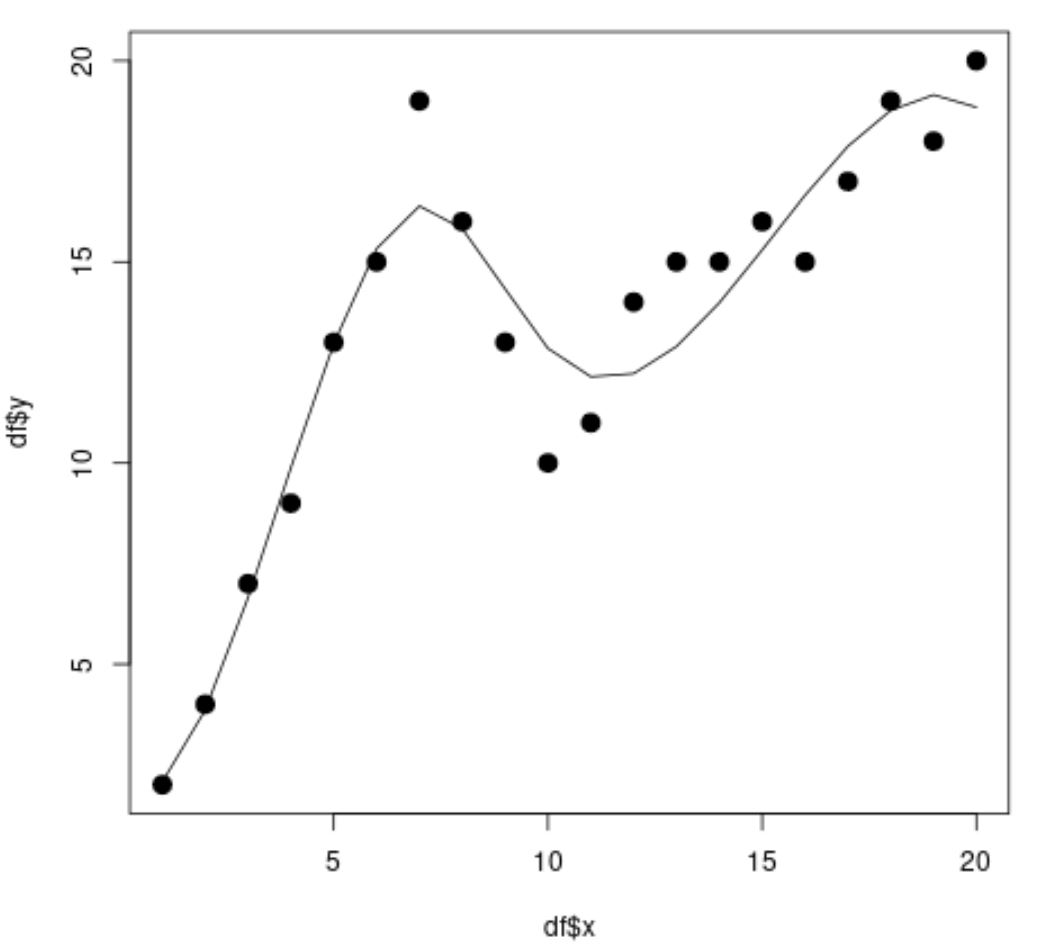
No gráfico de dispersão, podemos ver que o modelo de regressão spline é capaz de ajustar muito bem os dados.
A partir dos resultados do modelo, também podemos ver que o valor R-quadrado ajustado é 0,8987 .
O valor de R-quadrado ajustado para este modelo é muito maior do que o modelo de regressão linear simples, o que nos diz que o modelo de regressão spline é capaz de ajustar melhor os dados.
Observe que para este exemplo escolhemos que os nós estejam localizados em x=7 e x=10.
Na prática, você mesmo precisará escolher os locais dos nós com base em onde os padrões nos dados parecem mudar e com base em sua experiência no domínio.
Recursos adicionais
Os tutoriais a seguir explicam como realizar outras tarefas comuns em R:
Como realizar regressão linear múltipla em R
Como realizar regressão exponencial em R
Como realizar a regressão de mínimos quadrados ponderados em R