Distribuição hipergeométrica
Neste artigo explicamos o que é a distribuição hipergeométrica e como se calcula uma probabilidade com este tipo de distribuição. Você encontrará online a fórmula da distribuição hipergeométrica, quais são suas características, bem como uma calculadora para calcular a probabilidade da distribuição hipergeométrica.
Qual é a distribuição hipergeométrica?
A distribuição hipergeométrica é uma distribuição de probabilidade que descreve o número de casos de sucesso em uma extração aleatória sem substituição de n elementos de uma população.
Ou seja, a distribuição hipergeométrica é utilizada para calcular a probabilidade de obter x sucessos ao extrair n elementos de uma população sem substituir nenhum deles.
A distribuição hipergeométrica possui três parâmetros:
- N : é o número de elementos da população (N = 0, 1, 2,…).
- K : é o número máximo de casos de sucesso (K = 0, 1, 2,…,N). Como em uma distribuição hipergeométrica um elemento só pode ser considerado um “sucesso” ou um “fracasso”, NK é o número máximo de casos de falha.
- n : é o número de buscas sem substituição executadas.
![]()
Por exemplo, uma variável aleatória discreta X que tem uma distribuição hipergeométrica com parâmetros N=8, K=5 e n=3 é definida como segue:
![]()
Fórmula de distribuição hipergeométrica
A fórmula para a distribuição hipergeométrica é o produto do número combinatório de K sobre x pelo número combinatório de NK sobre nx dividido pelo número combinatório de N sobre n .

Onde N é o tamanho da população, K é o número total de casos favoráveis, n é o número de extrações sem reposição e x é o número de casos favoráveis para os quais a probabilidade de ocorrência deve ser calculada.
👉 Você pode usar a calculadora abaixo para calcular a probabilidade de um evento de uma variável que segue a distribuição hipergeométrica.
Exemplo de distribuição hipergeométrica
Depois de vermos a definição e a fórmula da distribuição hipergeométrica, agora resolveremos um exemplo passo a passo para que você saiba calcular a probabilidade de uma distribuição hipergeométrica.
- Em um saco colocamos 20 bolas azuis e 30 bolas vermelhas, ou seja, são 50 bolas no total dentro do saco. Se tirarmos 12 bolas sem substituir nenhuma, encontre a probabilidade de tirar 4 bolas azuis.
A primeira coisa que precisamos fazer para resolver o exercício é identificar os parâmetros da distribuição hipergeométrica. Neste caso, o número total de elementos da população é 50 ( N =50), o número máximo de casos favoráveis é 20 ( K =20) e são sorteadas 12 bolas ( n =12).
![Rendered by QuickLaTeX.com \left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)](https://statorials.org/wp-content/ql-cache/quicklatex.com-352132f74408eab99d3985c63a49f322_l3.png)
Queremos calcular a probabilidade de tirar 4 bolas azuis ( x =4), então aplicamos a fórmula de distribuição hipergeométrica, substituímos as variáveis pelos seus valores correspondentes e realizamos o cálculo:
![Rendered by QuickLaTeX.com P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-caf83b14deae0fe9882e4d40e677329f_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-ed747dd327149d4a925e6ad7c4119f81_l3.png)
Calculadora de distribuição hipergeométrica
Insira os parâmetros da distribuição hipergeométrica na calculadora online a seguir para calcular a probabilidade de ocorrência do evento desejado.
Lembre-se que N é o tamanho da população, K é o número total de casos favoráveis, n é o tamanho da amostra e x é o valor para o qual queremos encontrar a probabilidade de isso acontecer.
Características da distribuição hipergeométrica
A distribuição hipergeométrica tem as seguintes propriedades:
- O valor esperado de uma distribuição hipergeométrica é igual ao número de elementos da amostra multiplicado pelo número total de casos favoráveis dividido pelo número de elementos da população.
![]()
- A moda de uma distribuição hipergeométrica é o valor arredondado para baixo do produto de n+1 vezes K+1 dividido por N+2 .
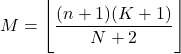
- A variância de uma distribuição hipergeométrica pode ser obtida usando a seguinte expressão:
![]()
- A função geradora de momento de uma distribuição hipergeométrica é a seguinte:
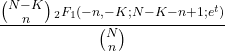
- A função característica da distribuição hipergeométrica é a seguinte:
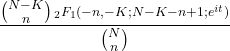
- A probabilidade de ocorrência de um determinado número de eventos pode ser calculada a partir da probabilidade do número anterior usando a recursiva para a distribuição hipergeométrica:
![]()
Distribuição hipergeométrica e distribuição binomial
A diferença entre a distribuição hipergeométrica e a distribuição binomial é a substituição. A distribuição hipergeométrica é usada quando as recuperações não são substituídas, porém, na distribuição binomial as recuperações são substituídas.
Por exemplo, se tirarmos cinco cartas aleatoriamente de um baralho e quisermos calcular a probabilidade de obter determinada carta, se não substituirmos cada carta que compramos, devemos utilizar a distribuição hipergeométrica para fazer o cálculo. Mas se ao retirar uma carta a colocamos de volta antes de realizar a próxima extração, então devemos usar a distribuição binomial para calcular a probabilidade.
Quando o número N é grande, a razão n/N é pequena e o número de casos favoráveis desejados é muito pequeno, podemos usar a distribuição hipergeométrica como uma aproximação da distribuição binomial. Porém, não recomendo porque o resultado não será tão confiável e, além disso, é mais fácil calcular probabilidades com a lei binomial do que com a lei hipergeométrica.