Como realizar regressão polinomial usando scikit-learn

A regressão polinomial é uma técnica que podemos usar quando o relacionamento entre uma variável preditora e uma variável de resposta é não linear.

Este tipo de regressão assume a forma:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² +… + β _h

onde h é o “grau” do polinômio.

O exemplo passo a passo a seguir mostra como realizar regressão polinomial em Python usando sklearn.

Etapa 1: crie os dados

Primeiro, vamos criar dois arrays NumPy para armazenar os valores de um preditor e de uma variável de resposta:

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

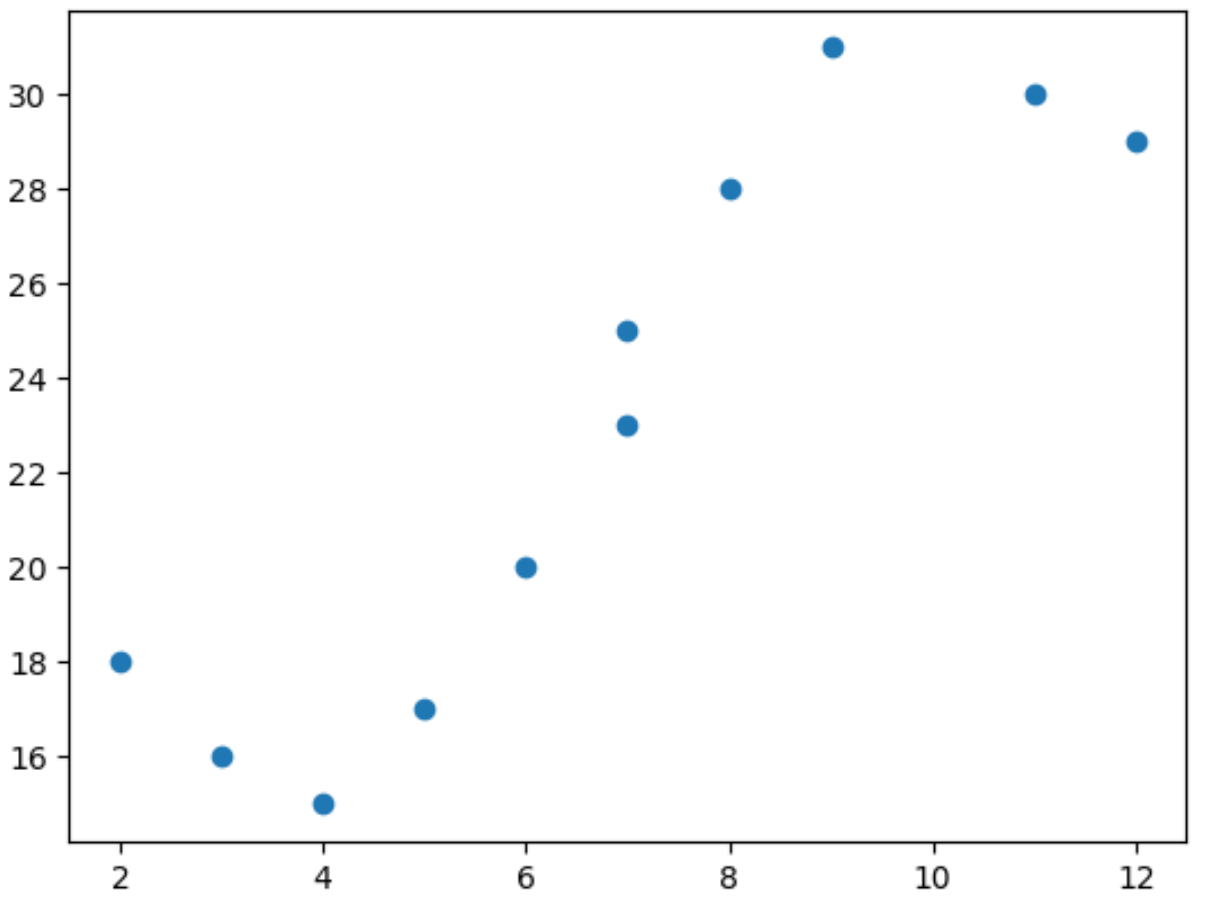
No gráfico de dispersão, podemos ver que a relação entre x e y não é linear.

Portanto, é uma boa ideia ajustar um modelo de regressão polinomial aos dados para capturar a relação não linear entre as duas variáveis.

Etapa 2: Ajustar o modelo de regressão polinomial

O código a seguir mostra como usar funções sklearn para ajustar um modelo de regressão polinomial de grau 3 a este conjunto de dados:

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

Usando os coeficientes do modelo mostrados na última linha, podemos escrever a equação de regressão polinomial ajustada da seguinte forma:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Esta equação pode ser usada para encontrar o valor esperado da variável de resposta dado um determinado valor da variável prevista.

Por exemplo, se x for 4, o valor esperado para a variável de resposta, y, seria 15,39:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39

Nota : Para ajustar um modelo de regressão polinomial com um grau diferente, basta alterar o valor do argumento de grau na função PolynomialFeatures() .

Etapa 3: Visualize o modelo de regressão polinomial

Finalmente, podemos criar um gráfico simples para visualizar o modelo de regressão polinomial ajustado aos pontos de dados originais:

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

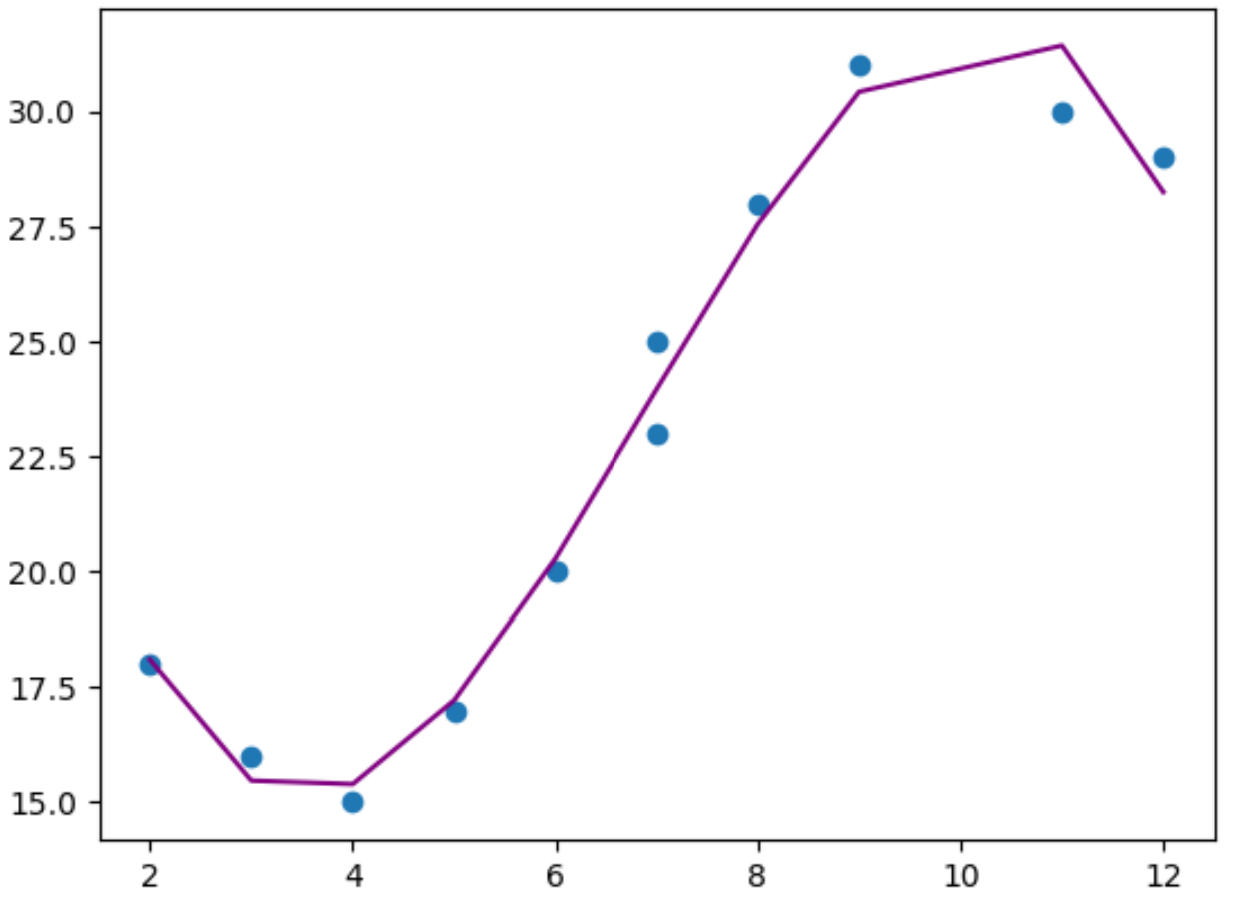
No gráfico, podemos ver que o modelo de regressão polinomial parece se ajustar bem aos dados, sem overfitting .

Observação : você pode encontrar a documentação completa da função sklearn PolynomialFeatures() aqui .

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras tarefas comuns usando o sklearn:

Como extrair coeficientes de regressão do sklearn
Como calcular a precisão balanceada usando sklearn
Como interpretar o relatório de classificação no Sklearn