Medidas de tendência central: definição e exemplos
Uma medida de tendência central é um valor único que representa o ponto central de um conjunto de dados. Este valor também pode ser chamado de “localização central” de um conjunto de dados.
Nas estatísticas, existem três medidas comuns de tendência central:
- A média
- A mediana
- A moda
Cada uma dessas medidas encontra a localização central de um conjunto de dados usando métodos diferentes. Dependendo do tipo de dados que você está analisando, pode ser melhor usar uma dessas três métricas em vez das outras duas.
Neste artigo, veremos como calcular cada uma das três medidas de tendência central e também como determinar qual medida é melhor usar com base em seus dados.
Por que as medidas de tendência central são úteis?
Antes de vermos como calcular a média, a mediana e a moda, é útil entender por que essas medidas são realmente úteis.
Considere o seguinte cenário:
Um jovem casal está tentando decidir onde comprar sua primeira casa em uma nova cidade e o máximo que podem gastar é US$ 150 mil. Algumas áreas da cidade têm casas caras, algumas têm casas baratas e algumas têm casas de preço médio. Eles desejam restringir facilmente sua pesquisa a bairros específicos que cabem em seu orçamento.
Se o casal apenas olhasse os preços das casas unifamiliares em cada bairro, poderia ter dificuldade em determinar quais bairros melhor se adaptam ao seu orçamento, porque poderia ver algo assim:
Preços das casas no bairro A : $ 140.000, $ 190.000, $ 265.000, $ 115.000, $ 270.000, $ 240.000, $ 250.000, $ 180.000, $ 160.000, $ 200.000, $ 240.000, $ 280.000,…
Preços das casas no bairro B : $ 140.000, $ 290.000, $ 155.000, $ 165.000, $ 280.000, $ 220.000, $ 155.000, $ 185.000, $ 160.000, $ 200.000, $ 190.000, $ 140.000, $ 145,0 0 0,…
Preços das casas no bairro C : $ 140.000, $ 130.000, $ 165.000, $ 115.000, $ 170.000, $ 100.000, $ 150.000, $ 180.000, $ 190.000, $ 120.000, $ 110.000, $ 130.000, $ 120,0 0 0,…
No entanto, se conhecessem o preço médio (por exemplo, uma medida de tendência central) das casas em cada bairro, então poderiam refinar a sua pesquisa muito mais rapidamente porque poderiam identificar mais facilmente qual bairro tem preços de casas que correspondem ao seu orçamento:
Preço médio de uma casa no bairro A: US$ 220 mil
Preço médio de uma casa no bairro B : $ 190.000
Preço médio de uma casa no bairro C : $ 140.000
Ao conhecer o preço médio das casas em cada bairro, eles podem ver rapidamente que o Bairro C provavelmente terá o maior número de casas disponíveis dentro do seu orçamento.
Este é o benefício de usar uma medida de tendência central: ajuda a entender o valor central de um conjunto de dados, que tende a descrever onde geralmente estão os valores dos dados. Neste exemplo específico, ajuda o jovem casal a compreender o preço típico de uma casa em cada bairro.
Conclusão: uma medida de tendência central é útil porque nos fornece um valor único que descreve o “centro” de um conjunto de dados. Isso nos ajuda a entender um conjunto de dados com muito mais rapidez do que apenas observar todos os valores individuais no conjunto de dados.
Significar
A medida de tendência central mais comumente usada é a média . Para calcular a média de um conjunto de dados, basta somar todos os valores individuais e dividir pelo número total de valores.
Média = (soma de todos os valores) / (número total de valores)
Por exemplo, suponha que temos o seguinte conjunto de dados que mostra o número de home runs rebatidos por 10 jogadores de beisebol do mesmo time durante uma temporada:
| Jogador | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dez |
|---|---|---|---|---|---|---|---|---|---|---|
| Home runs | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
O número médio de home runs rebatidos por jogador pode ser calculado da seguinte forma:
Média = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 circuitos .
Mediana
A mediana é o valor médio de um conjunto de dados. Você pode encontrar a mediana ordenando todos os valores individuais em um conjunto de dados do menor para o maior e encontrando o valor mediano. Se houver um número ímpar de valores, a mediana é o valor do meio. Se houver um número par de valores, a mediana será a média dos dois valores intermediários.
Por exemplo, para encontrar o número médio de home runs rebatidos pelos 10 jogadores de beisebol do exemplo anterior, podemos classificar os jogadores em ordem decrescente do número de home runs rebatidos:
| Jogador | #1 | #6 | #7 | #5 | #dez | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Home runs | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Como temos um número par de valores, a mediana é simplesmente a média dos dois valores intermediários: 13,5 .
Em vez disso, considere se tivéssemos nove jogadores:
| Jogador | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Home runs | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
Neste caso, como temos um número ímpar de valores, a mediana é simplesmente o valor do meio: 14 .
A moda
A moda é o valor que aparece com mais frequência em um conjunto de dados. Um conjunto de dados não pode ter modos (se nenhum valor se repetir), um modo ou vários modos.
Por exemplo, o seguinte conjunto de dados não tem moda:
| Jogador | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dez |
|---|---|---|---|---|---|---|---|---|---|---|
| Home runs | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
O seguinte conjunto de dados possui uma moda: 15 . Este é o valor que aparece com mais frequência.
| Jogador | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dez |
|---|---|---|---|---|---|---|---|---|---|---|
| Home runs | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
O conjunto de dados a seguir possui três modos: 8, 15, 19 . Estes são os valores que aparecem com mais frequência.
| Jogador | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dez |
|---|---|---|---|---|---|---|---|---|---|---|
| Home runs | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
A moda pode ser uma medida de tendência central particularmente útil quando se trabalha com dados categóricos, porque nos diz qual categoria aparece com mais frequência. Por exemplo, considere o seguinte gráfico de barras que mostra os resultados de uma pesquisa sobre a cor favorita das pessoas:
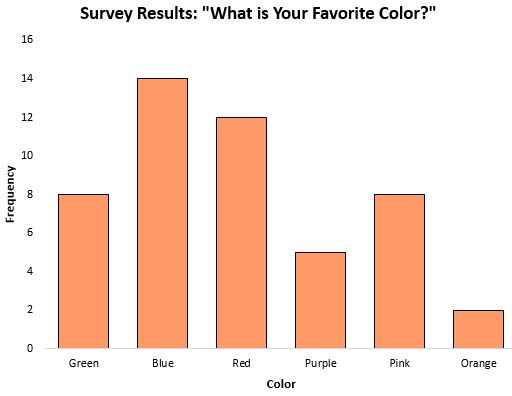
A moda , ou a resposta que ocorreu com mais frequência, foi azul.
Em cenários onde os dados são categóricos (como o acima), nem é possível calcular a mediana ou média, portanto a moda é a única medida de tendência central que podemos utilizar.
O modo também pode ser usado para dados numéricos, como vimos no exemplo acima com jogadores de beisebol. No entanto, a moda tende a ser menos útil para responder à pergunta “Qual é um valor típico para este conjunto de dados?” »
Por exemplo, suponha que queiramos saber o número típico de home runs rebatidos por um jogador de beisebol deste time:
| Jogador | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dez |
|---|---|---|---|---|---|---|---|---|---|---|
| Home runs | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
A moda para este conjunto de dados é 8, 15 e 19 porque estes são os valores mais frequentes. No entanto, estes não são muito úteis para compreender o número típico de home runs rebatidos por um jogador da equipa. Uma melhor medida de tendência central neste caso seria a mediana (15) ou a média (também 15).
A moda também é uma medida pobre de tendência central quando é um número distante do restante dos valores. Por exemplo, o modo do conjunto de dados a seguir é 30, mas na verdade não representa o número “típico” de home runs por jogador do time:
| Jogador | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dez |
|---|---|---|---|---|---|---|---|---|---|---|
| Home runs | 5 | 6 | 7 | dez | 11 | 12 | 13 | 15 | 30 | 30 |
Novamente, a média ou mediana descreveria melhor a localização central deste conjunto de dados.
Quando usar média, mediana e modo
Vimos que a média, a mediana e a moda medem a localização central, ou “valor típico”, de um conjunto de dados de maneiras muito diferentes:
Média: Encontra o valor médio em um conjunto de dados.
Mediana: Encontra o valor mediano em um conjunto de dados.
Modo: Encontra o valor mais frequente em um conjunto de dados.
Aqui estão os cenários em que certas medidas de tendência central são melhores para usar do que outras:
Quando usar a média
É melhor usar a média quando a distribuição dos dados for bastante simétrica e não houver valores discrepantes.
Por exemplo, suponha que temos a seguinte distribuição que mostra os salários dos indivíduos em uma determinada cidade:

Dado que esta distribuição é bastante simétrica (ou seja, se a dividirmos ao meio, cada metade parecerá aproximadamente igual) e não existem valores discrepantes (ou seja, (digamos, não há salários extremamente elevados), a média fará um bom trabalho ao descrever este conjunto de dados.
A média acaba sendo de US$ 63.000, que fica aproximadamente no centro da distribuição:

Quando usar a mediana
É melhor usar a mediana quando a distribuição dos dados é distorcida ou quando há valores discrepantes.
Dados tendenciosos:
Quando a distribuição é distorcida, a mediana ainda consegue capturar a localização central. Por exemplo, considere a seguinte distribuição de salários de indivíduos em uma determinada cidade:

A mediana reflete melhor o salário “típico” de um indivíduo do que a média. Isso ocorre porque valores grandes na cauda de uma distribuição tendem a afastar a média do centro e em direção à cauda longa.
Neste exemplo específico, a média diz-nos que um indivíduo típico ganha cerca de 47.000 dólares por ano nesta cidade, enquanto a mediana diz-nos que o indivíduo típico ganha apenas cerca de 32.000 dólares por ano, o que é muito mais representativo do indivíduo típico.
Valores discrepantes:
A mediana também ajuda a capturar melhor a localização central de uma distribuição quando há valores discrepantes nos dados. Por exemplo, considere o gráfico a seguir que mostra a metragem quadrada das casas em uma determinada rua:

A média é fortemente influenciada por algumas casas extremamente grandes, enquanto a mediana não. Assim, a mediana captura melhor a metragem quadrada “típica” de uma casa naquela rua do que a média.
Quando usar o modo
Este modo é melhor usado quando você está trabalhando com dados categóricos e deseja saber qual categoria aparece com mais frequência. aqui estão alguns exemplos:
- Você está realizando uma pesquisa sobre as cores favoritas das pessoas e quer saber qual cor aparece com mais frequência nas respostas.
- Você está conduzindo uma pesquisa sobre as preferências das pessoas entre três opções de design de site e deseja saber qual design as pessoas preferem mais.
Conforme mencionado anteriormente, se você estiver trabalhando com dados categóricos, nem é possível calcular a mediana ou média, o que deixa a moda como a única medida de tendência central.
Em geral, se você estiver trabalhando com dados numéricos, como metragem quadrada de casas, número de home runs rebatidos por jogador, salário por indivíduo, etc., geralmente é melhor usar a mediana ou média para descrever o valor “típico” em o conjunto de dados.
Nota: É importante observar que se um conjunto de dados for perfeitamente distribuído normalmente, então a média, a mediana e a moda terão todos o mesmo valor.