Introdução à regressão linear simples

A regressão linear simples é um método estatístico que você pode usar para compreender a relação entre duas variáveis, x e y.

Uma variável, x , é conhecida como variável preditora .

A outra variável, y , é conhecida como variável de resposta .

Por exemplo, suponha que temos o seguinte conjunto de dados com peso e altura de sete indivíduos:

Seja o peso a variável preditora e a altura a variável resposta.

Se representarmos graficamente essas duas variáveis usando um gráfico de dispersão, com peso no eixo x e altura no eixo y, seria assim:

Suponha que queiramos entender a relação entre peso e altura. No gráfico de dispersão podemos ver claramente que à medida que o peso aumenta, a altura também tende a aumentar, mas para realmente quantificar esta relação entre peso e altura precisamos usar a regressão linear.

Usando a regressão linear, podemos encontrar a linha que melhor “se ajusta” aos nossos dados. Esta linha é conhecida como linha de regressão de mínimos quadrados e pode ser usada para nos ajudar a compreender as relações entre peso e altura.

Normalmente, você usará software como Microsoft Excel, SPSS ou uma calculadora gráfica para encontrar a equação desta reta.

A fórmula para a linha de melhor ajuste está escrita:

ŷ=b ₀ + b ₁ x

onde ŷ é o valor previsto da variável de resposta, b ₀ é o intercepto, b ₁ é o coeficiente de regressão e x é o valor da variável preditora.

Relacionado: 4 exemplos de uso de regressão linear na vida real

Encontre a “linha mais adequada”

Para este exemplo, podemos simplesmente inserir nossos dados na calculadora estatística de regressão linear e pressionar Calcular :

A calculadora encontra automaticamente a linha de regressão de mínimos quadrados :

ŷ = 32,7830 + 0,2001x

Se diminuirmos o zoom do nosso gráfico de dispersão anterior e adicionarmos esta linha ao gráfico, ele ficaria assim:

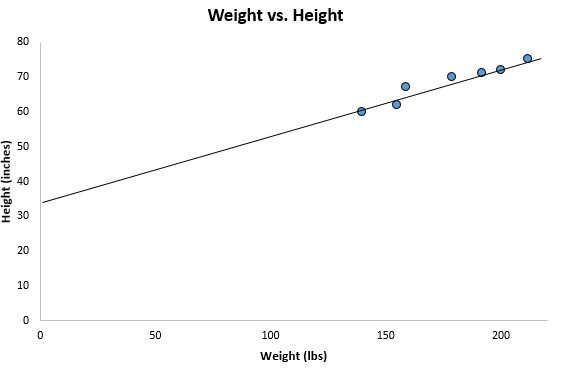
Observe como nossos pontos de dados estão espalhados em torno desta linha. Na verdade, esta recta de regressão de mínimos quadrados é a recta mais adequada aos nossos dados entre todas as rectas possíveis que poderíamos traçar.

Como interpretar uma linha de regressão de mínimos quadrados

Veja como interpretar esta linha de regressão de mínimos quadrados: ŷ = 32,7830 + 0,2001x

_b0 = 32,7830 . Isso significa que quando o peso da variável preditora é zero libra, a altura prevista é 32,7830 polegadas. Às vezes, pode ser útil saber o valor de b ₀ , mas neste exemplo específico não faz sentido interpretar b ₀ , uma vez que uma pessoa não pode pesar zero quilo.

_b1 = 0,2001 . Isto significa que um aumento de uma unidade em x está associado a um aumento de 0,2001 unidades em y . Neste caso, um aumento no peso de meio quilo está associado a um aumento na altura de 0,2001 polegada.

Como usar a linha de regressão de mínimos quadrados

Usando esta linha de regressão de mínimos quadrados, podemos responder a perguntas como:

Para alguém que pesa 170 libras, qual a altura que devemos esperar que ela tenha?

Para responder a esta questão, podemos simplesmente inserir 170 na nossa linha de regressão para x e resolver para y:

ŷ = 32,7830 + 0,2001(170) = 66,8 polegadas

Para alguém que pesa 150 libras, qual a altura que devemos esperar que ela tenha?

Para responder a esta questão, podemos inserir 150 na nossa linha de regressão para x e resolver para y:

ŷ = 32,7830 + 0,2001(150) = 62,798 polegadas

Cuidado: Ao usar uma equação de regressão para responder a perguntas como essas, certifique-se de usar apenas valores para a variável preditora que estejam dentro do intervalo da variável preditora no conjunto de dados. origem que usamos para gerar a linha de regressão de mínimos quadrados. Por exemplo, os pesos no nosso conjunto de dados variaram entre 140 e 212 libras. Portanto, faz sentido responder a perguntas sobre a altura esperada quando o peso está entre 140 e 212 libras.

O coeficiente de determinação

Uma forma de medir até que ponto a linha de regressão de mínimos quadrados “se ajusta” aos dados é utilizar o coeficiente de determinação , denotado por R ² .

O coeficiente de determinação é a proporção da variância na variável resposta que pode ser explicada pela variável preditora.

O coeficiente de determinação pode variar de 0 a 1. Um valor 0 indica que a variável resposta não pode ser explicada pela variável preditora. Um valor 1 indica que a variável resposta pode ser perfeitamente explicada sem erros pela variável preditora.

Um R ² entre 0 e 1 indica até que ponto a variável resposta pode ser explicada pela variável preditora. Por exemplo, um R ² de 0,2 indica que 20% da variância na variável resposta pode ser explicada pela variável preditora; um R ² de 0,77 indica que 77% da variância na variável resposta pode ser explicada pela variável preditora.

Observe que em nosso resultado anterior obtivemos um R ² de 0,9311, o que indica que 93,11% da variabilidade da altura pode ser explicada pela variável preditora peso:

Isso nos diz que o peso é um bom indicador de altura.

Suposições de regressão linear

Para que os resultados de um modelo de regressão linear sejam válidos e confiáveis, devemos verificar se as quatro premissas a seguir são atendidas:

1. Relacionamento linear: Existe um relacionamento linear entre a variável independente, x, e a variável dependente, y.

2. Independência: Os resíduos são independentes. Em particular, não há correlação entre resíduos consecutivos em dados de séries temporais.

3. Homocedasticidade: Os resíduos possuem variância constante em cada nível de x.

4. Normalidade: Os resíduos do modelo são normalmente distribuídos.

Se um ou mais destes pressupostos não forem cumpridos, os resultados da nossa regressão linear podem não ser fiáveis ou mesmo enganosos.

Consulte este artigo para obter uma explicação de cada suposição, como determinar se a suposição foi atendida e o que fazer se a suposição não for atendida.