Anova unidirecional: definição, fórmula e exemplo
Uma ANOVA unidirecional (“análise de variância”) compara as médias de três ou mais grupos independentes para determinar se existe uma diferença estatisticamente significativa entre as médias da população correspondente.
Este tutorial explica o seguinte:
- A motivação para realizar uma ANOVA unidirecional.
- As suposições que devem ser atendidas para realizar uma ANOVA unidirecional.
- O processo para realizar uma ANOVA unidirecional.
- Um exemplo de como realizar uma ANOVA unidirecional.
ANOVA unidirecional: motivação
Suponha que queiramos saber se três programas diferentes de preparação para testes levam ou não a notas médias diferentes no vestibular. Como há milhões de estudantes do ensino médio em todo o país, seria muito demorado e caro ir até cada aluno e deixá-los usar um dos programas de preparação para testes.
Em vez disso, poderíamos selecionar três amostras aleatórias de 100 estudantes da população e permitir que cada amostra usasse um dos três programas de preparação para o exame. Então poderíamos registrar as notas de cada aluno depois que eles fizerem o exame.
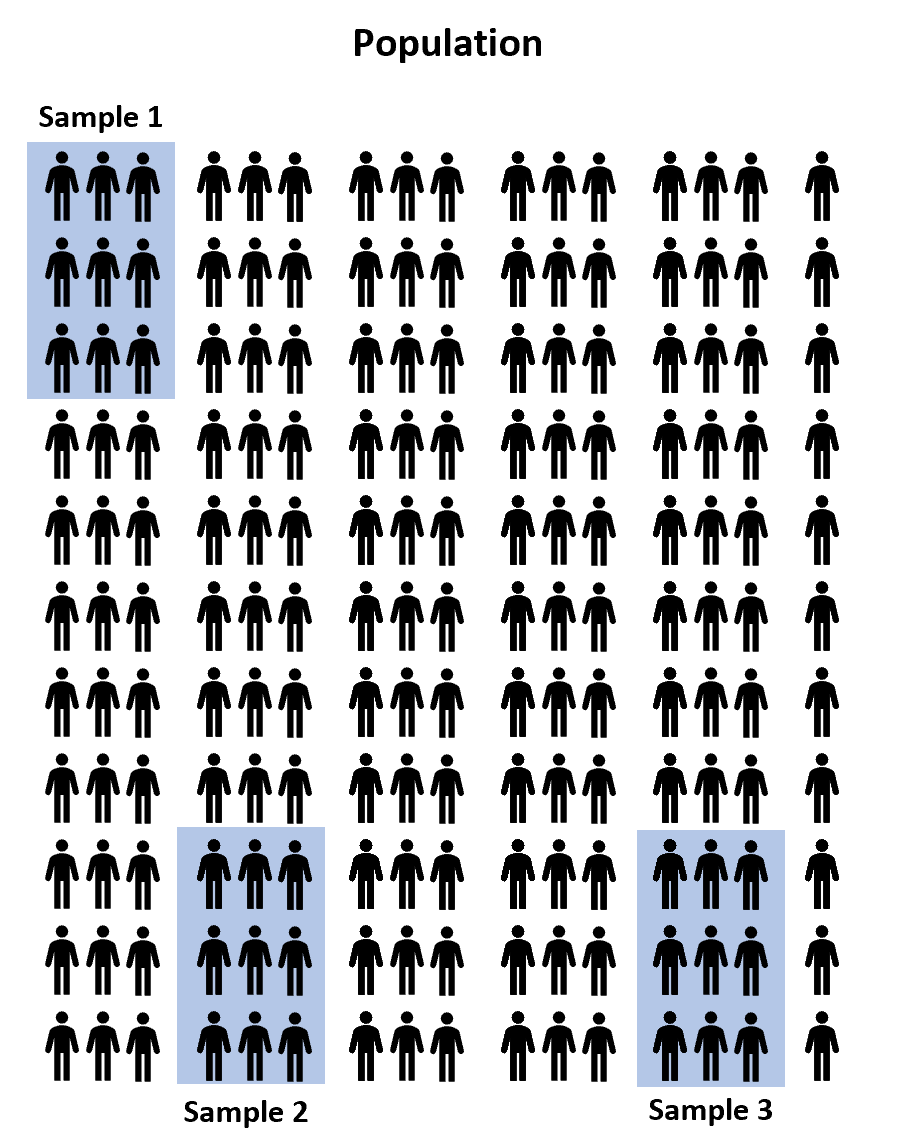
No entanto, é praticamente garantido que a pontuação média do exame entre as três amostras será pelo menos um pouco diferente. A questão é se esta diferença é estatisticamente significativa . Felizmente, uma ANOVA unilateral permite-nos responder a esta questão.
ANOVA unidirecional: suposições
Para que os resultados de uma ANOVA unidirecional sejam válidos, as seguintes suposições devem ser atendidas:
1. Normalidade – Cada amostra foi retirada de uma população normalmente distribuída.
2. Variâncias iguais – As variâncias das populações das quais as amostras são extraídas são iguais. Você pode usar o teste de Bartlett para testar essa hipótese.
3. Independência – As observações dentro de cada grupo são independentes umas das outras e as observações dentro dos grupos foram obtidas por amostragem aleatória.
Leia este artigo para obter mais detalhes sobre como verificar essas suposições.
ANOVA unidirecional: o processo
Uma ANOVA unidirecional usa as seguintes hipóteses nulas e alternativas:
- H 0 (hipótese nula): μ 1 = μ 2 = μ 3 = … = μ k (todas as médias populacionais são iguais)
- H 1 (hipótese alternativa): pelo menos uma média populacional é diferente descansar
Normalmente, você usará algum software estatístico (como R, Excel, Stata, SPSS, etc.) para realizar ANOVA unidirecional porque é tedioso realizá-lo manualmente.
Independentemente do software que você usa, você receberá a seguinte tabela como saída:
| Fonte | Soma dos quadrados (SS) | df | Quadrados médios (MS) | F | p |
|---|---|---|---|---|---|
| Tratamento | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Erro | ESE | df e | MSE | ||
| Total | SST | dft |
Ouro:
- SSR: regressão da soma dos quadrados
- SSE: soma do erro quadrático
- SST: soma total dos quadrados (SST = SSR + SSE)
- df r : graus de liberdade de regressão (df r = k-1)
- df e : graus de liberdade de erro (df e = nk)
- df t : graus totais de liberdade (df t = n-1)
- k: número total de grupos
- n: total de observações
- MSR: regressão quadrática média (MSR = SSR/df r )
- MSE: erro quadrático médio (MSE = SSE/df e )
- F: A estatística do teste F (F = MSR/MSE)
- p: O valor p que corresponde a F dfr, dfe
Se o valor p for menor que o nível de significância escolhido (por exemplo, 0,05), então você pode rejeitar a hipótese nula e concluir que pelo menos uma das médias da população é diferente das outras.
Nota: Se você rejeitar a hipótese nula, isso indica que pelo menos uma das médias populacionais é diferente das outras, mas a tabela ANOVA não especifica quais médias populacionais são diferentes. Para determinar isso, você precisa realizar testes post hoc , também chamados de testes de “comparação múltipla”.
ANOVA unidirecional: exemplo
Suponha que queiramos saber se três programas diferentes de preparação para testes levam ou não a pontuações médias diferentes em um determinado exame. Para testar isso, recrutamos 30 estudantes para participar de um estudo e os dividimos em três grupos.
Os alunos de cada grupo são designados aleatoriamente para usar um dos três programas de preparação para testes nas três semanas seguintes para se prepararem para um exame. No final das três semanas, todos os alunos fazem o mesmo exame.
Os resultados dos exames para cada grupo são mostrados abaixo:

Para realizar uma ANOVA unidirecional nesses dados, usaremos a calculadora estatística ANOVA unidirecional com a seguinte entrada:

Na tabela de saída, vemos que a estatística do teste F é 2,358 e o valor p correspondente é 0,11385 .

Como esse valor p não é inferior a 0,05, não rejeitamos a hipótese nula.
Isto significa que não temos evidências suficientes para afirmar que existe uma diferença estatisticamente significativa entre as notas médias dos exames dos três grupos.
Recursos adicionais
Os artigos a seguir explicam como realizar uma ANOVA unidirecional usando diferentes softwares estatísticos:
Como realizar ANOVA unidirecional no Excel
Como realizar ANOVA unidirecional em R
Como realizar ANOVA unidirecional em Python
Como realizar ANOVA unidirecional no SAS
Como realizar ANOVA unidirecional no SPSS
Como realizar ANOVA unidirecional no Stata
Como realizar ANOVA unidirecional em uma calculadora TI-84
Calculadora ANOVA unidirecional on-line