Como realizar a regressão passo a passo no sas (com exemplo)
A regressão passo a passo é um procedimento que podemos usar para construir um modelo de regressão a partir de um conjunto de variáveis preditoras, inserindo e removendo preditores passo a passo no modelo até que n Não haja mais uma razão estatisticamente válida para inserir ou exclua mais.
O objetivo da regressão stepwise é criar um modelo de regressão que inclua todas as variáveis preditoras que estão estatisticamente relacionadas de forma significativa à variável de resposta .
Para realizar a regressão passo a passo no SAS, você pode usar PROC REG com a instrução SELECTION .
O exemplo a seguir mostra como realizar a regressão stepwise no SAS na prática.
Exemplo: realizando uma regressão passo a passo no SAS
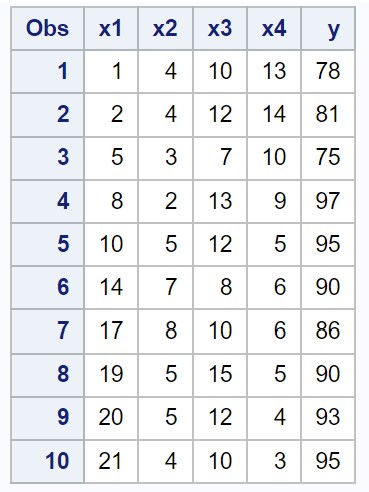
Suponha que temos o seguinte conjunto de dados no SAS que contém quatro variáveis preditoras (x1, x2, x3, x4) e uma variável de resposta (y):
/*create dataset*/ data my_data; input x1 x2 x3 x4 y; datalines ; 1 4 10 13 78 2 4 12 14 81 5 3 7 10 75 8 2 13 9 97 10 5 12 5 95 14 7 8 6 90 17 8 10 6 86 19 5 15 5 90 20 5 12 4 93 21 4 10 3 95 ; run ; /*view dataset*/ proc print data =my_data;
Agora, suponha que queiramos determinar qual combinação de variáveis preditoras produzirá o melhor modelo de regressão linear múltipla .
Quando falamos sobre o “melhor” modelo de regressão, queremos dizer o modelo que maximiza ou minimiza certas medidas.
Existem duas métricas que normalmente usamos para avaliar qual modelo de regressão é melhor entre um grupo de modelos potenciais:
1. R-quadrado ajustado : O valor de R-quadrado ajustado nos diz a utilidade de um modelo, ajustado com base no número de preditores em um modelo. O modelo com maior valor de R-quadrado ajustado é considerado o melhor.
2. AIC : O Critério de Informação de Akaike (AIC) é uma métrica usada para comparar o ajuste de diferentes modelos de regressão. O modelo com menor valor de AIC é considerado o melhor.
Felizmente, podemos calcular os valores ajustados de R-quadrado e AIC para modelos de regressão no SAS usando PROC REG com a instrução SELECTION .
O código a seguir mostra como fazer isso:
/*perform stepwise multiple linear regression*/ proc reg data =my_data outest =est; model y=x1 x2 x3 x4 / selection=adjrsq aic ; output out =out p=pr=r; run ; quit ;
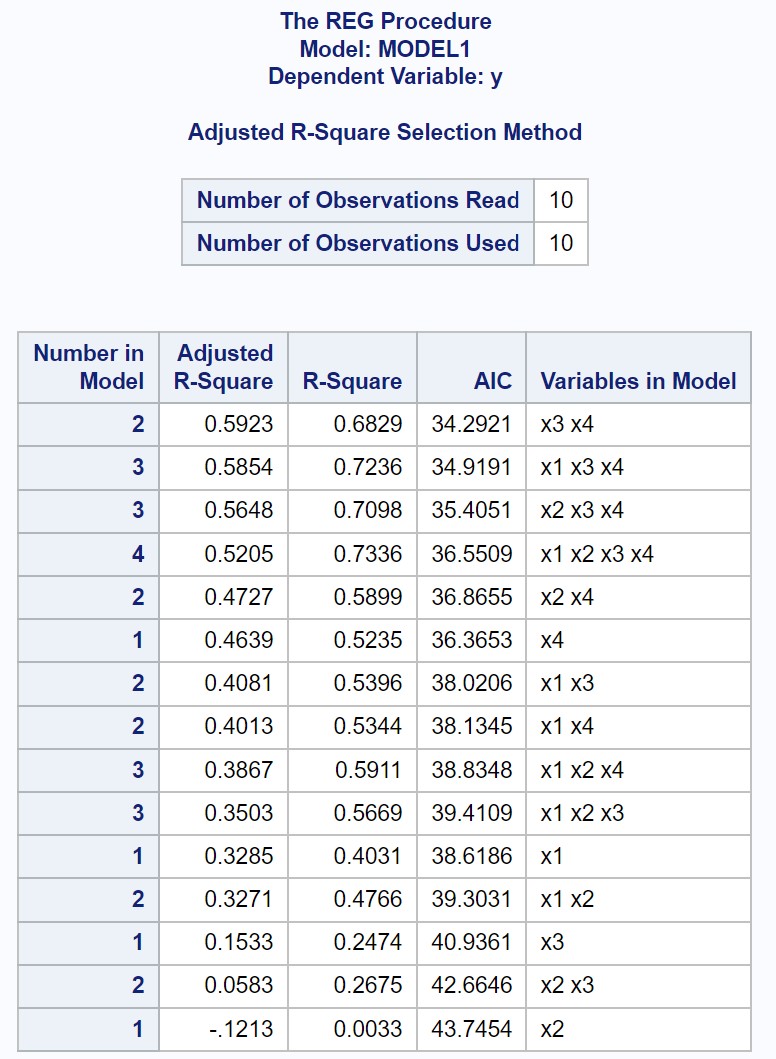
A saída exibe os valores ajustados de R-quadrado e AIC para cada modelo de regressão linear múltipla possível.
Pelo resultado, podemos perceber que o valor com maior valor de R quadrado ajustado e menor valor de AIC é o modelo de regressão que utiliza apenas x3 e x4 como variáveis preditoras.
Assim, declaramos que o seguinte modelo é “o melhor” entre todos os modelos possíveis:
y = b 0 + b 1 (x3) + b 2 (x4)
Este modelo de regressão específico possui as seguintes métricas:
- Valor R-quadrado ajustado: 0,5923
- AIC: 34.2921
Notas sobre a seleção do “melhor” modelo de regressão
Observe que às vezes o modelo com o maior valor de R-quadrado ajustado nem sempre também possui o menor valor de AIC.
Quando se trata de decidir qual modelo de regressão é o melhor, o R-quadrado ajustado e o AIC servem como sugestões, mas no mundo real pode ser necessário usar conhecimentos de domínio para determinar qual modelo é o melhor.
Também pode ser sensato escolher um modelo parcimonioso , ou seja, um modelo que atinja um nível de ajuste desejado usando o menor número possível de variáveis preditoras.
O raciocínio por trás deste tipo de modelo decorre da ideia da navalha de Occam (às vezes chamada de “princípio da parcimônia”) que diz que a explicação mais simples é provavelmente a correta.
Aplicado às estatísticas, um modelo que possui poucos parâmetros, mas atinge um nível de ajuste satisfatório, deve ser preferido a um modelo que possui muitos parâmetros e atinge apenas um nível de ajuste ligeiramente superior.
Recursos adicionais
Os tutoriais a seguir explicam como executar outras tarefas comuns no SAS:
Como realizar regressão linear simples no SAS
Como realizar regressão linear múltipla no SAS
Como realizar regressão polinomial no SAS
Como realizar regressão logística no SAS