Como extrair resíduos da função lm() em r

Você pode usar a seguinte sintaxe para extrair resíduos da função lm() em R:

 fit$residuals

Este exemplo pressupõe que usamos a função lm() para ajustar um modelo de regressão linear e nomeamos os resultados como fit .

O exemplo a seguir mostra como usar essa sintaxe na prática.

Relacionado:Como extrair o R-quadrado da função lm() em R

Exemplo: como extrair resíduos de lm() em R

Suponha que temos o seguinte quadro de dados em R que contém informações sobre minutos jogados, total de faltas e total de pontos marcados por 10 jogadores de basquete:

 #create data frame
df <- data. frame (minutes=c(5, 10, 13, 14, 20, 22, 26, 34, 38, 40),
                 fouls=c(5, 5, 3, 4, 2, 1, 3, 2, 1, 1),
                 points=c(6, 8, 8, 7, 14, 10, 22, 24, 28, 30))

#view data frame
df

   minutes fouls points
1 5 5 6
2 10 5 8
3 13 3 8
4 14 4 7
5 20 2 14
6 22 1 10
7 26 3 22
8 34 2 24
9 38 1 28
10 40 1 30

Suponha que queiramos ajustar o seguinte modelo de regressão linear múltipla:

pontos = β ₀ + β ₁ (minutos) + β ₂ (faltas)

Podemos usar a função lm() para ajustar este modelo de regressão:

 #fit multiple linear regression model
fit <- lm(points ~ minutes + fouls, data=df)

Podemos então digitar fit$residuals para extrair os resíduos do modelo:

 #extract residuals from model
fit$residuals

         1 2 3 4 5 6 7 
 2.0888729 -0.7982137 0.6371041 -3.5240982 1.9789676 -1.7920822 1.9306786 
         8 9 10 
-1.7048752 0.5692404 0.6144057

Como houve 10 observações no total em nosso banco de dados, existem 10 resíduos – um para cada observação.

Por exemplo:

• A primeira observação tem um resíduo de 2.089 .
• A segunda observação tem um resíduo de -0,798 .
• A terceira observação tem um resíduo de 0,637 .

E assim por diante.

Podemos então criar um gráfico dos resíduos em relação aos valores ajustados, se desejarmos:

 #store residuals in variable
res <- fit$residuals

#produce residual vs. fitted plot
plot(fitted(fit), res)

#add a horizontal line at 0 
abline(0,0)

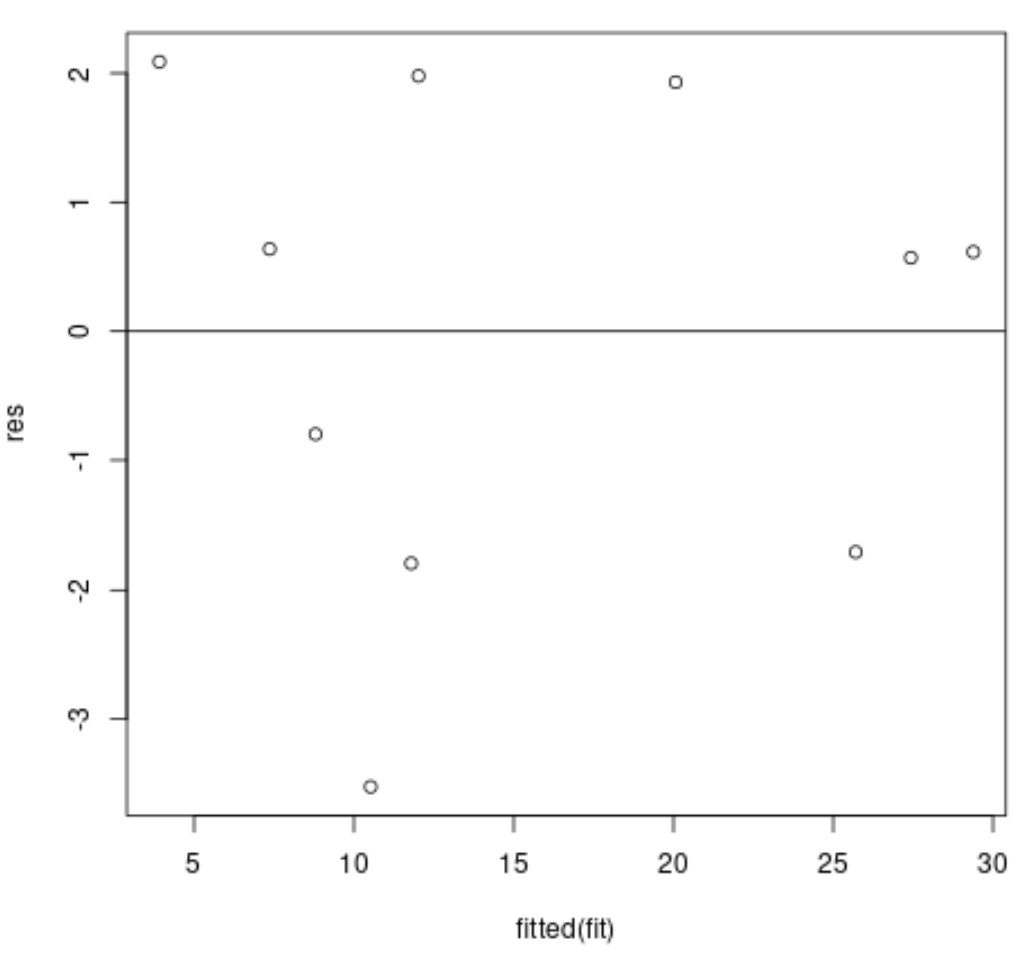
O eixo x exibe os valores ajustados e o eixo y exibe os resíduos.

Idealmente, os resíduos deveriam ser espalhados aleatoriamente em torno de zero, sem um padrão claro, para garantir que a suposição de homocedasticidade seja atendida.

No gráfico de resíduos acima, podemos ver que os resíduos parecem estar espalhados aleatoriamente em torno de zero, sem um padrão claro, o que significa que a suposição de homocedasticidade provavelmente é atendida.

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras tarefas comuns em R:

Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como criar um gráfico residual em R