Coeficiente de correlação de pearson

O coeficiente de correlação de Pearson (também conhecido como “coeficiente de correlação produto-momento”) é uma medida da associação linear entre duas variáveis X e Y. Tem um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

A fórmula para encontrar o coeficiente de correlação de Pearson

A fórmula para encontrar o coeficiente de correlação de Pearson, denotado r , para uma amostra de dados é ( via Wikipedia ):

Você provavelmente nunca terá que calcular essa fórmula manualmente, pois pode usar um software para fazer isso por você, mas é útil entender o que exatamente essa fórmula faz examinando um exemplo.

Suponha que temos o seguinte conjunto de dados:

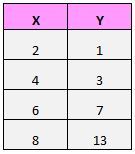
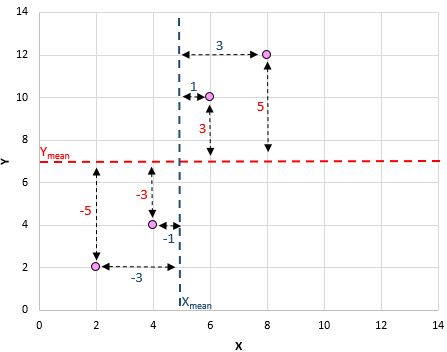
Se plotarmos esses pares (X, Y) em um gráfico de dispersão, ficaria assim:

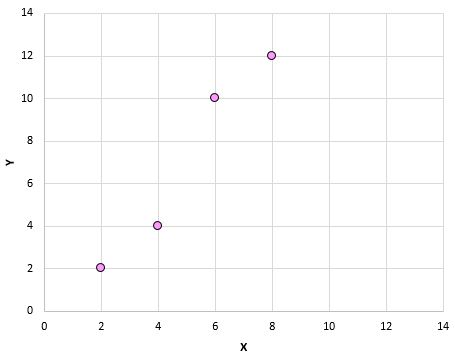
Apenas olhando para este gráfico de dispersão, podemos ver que existe uma associação positiva entre as variáveis X e Y: à medida que X aumenta, Y tende a aumentar também. Mas para quantificar exactamente o quão positivamente estas duas variáveis estão associadas, precisamos de encontrar o coeficiente de correlação de Pearson.

Vamos nos concentrar apenas no numerador da fórmula:

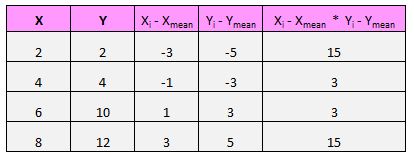
Para cada par (X, Y) em nosso conjunto de dados, precisamos encontrar a diferença entre o valor x e o valor médio de x, a diferença entre o valor y e o valor médio de y e, em seguida, multiplicar esses dois números.

Por exemplo, nosso primeiro par (X, Y) é (2, 2). O valor médio de x neste conjunto de dados é 5 e o valor médio de y neste conjunto de dados é 7. Portanto, a diferença entre o valor de x deste par e o valor médio de x é 2 – 5 = -3. A diferença entre o valor y deste par e o valor médio de y é 2 – 7 = -5. Então, quando multiplicamos esses dois números, obtemos -3 * -5 = 15.

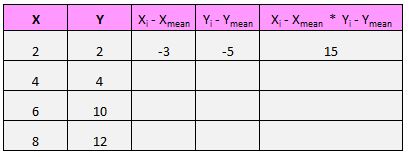
Aqui está uma visão geral do que acabamos de fazer:

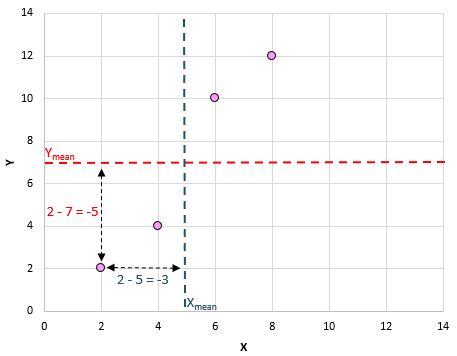
Depois é só fazer isso para cada par:

A etapa final para obter o numerador da fórmula é simplesmente somar todos esses valores:

15 + 3 +3 + 15 = 36

Então, o denominador da fórmula nos diz para encontrar a soma de todas as diferenças quadradas para x e y, depois multiplicar esses dois números e, em seguida, calcular a raiz quadrada:

Então, primeiro encontraremos a soma dos quadrados das diferenças para x e y:

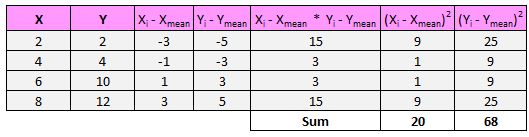
A seguir, multiplicaremos esses dois números: 20 * 68 = 1.360.

Por fim, tiraremos a raiz quadrada: √ 1.360 = 36,88

Então descobrimos que o numerador da fórmula é 36 e o denominador é 36,88. Isso significa que nosso coeficiente de correlação de Pearson é r = 36/36,88 = 0,976

Este número está próximo de 1, indicando que existe uma forte relação linear positiva entre nossas variáveis X e Y. Isso confirma a relação que observamos no gráfico de dispersão.

Ver correlações

Lembre-se de que um coeficiente de correlação de Pearson nos diz o tipo de relação linear (positiva, negativa, nenhuma) entre duas variáveis, bem como a força dessa relação (fraca, moderada, forte).

Quando criamos um gráfico de dispersão de duas variáveis, podemos ver a relação real entre duas variáveis. Aqui estão os muitos tipos de relações lineares que podemos observar:

Relação forte e positiva: à medida que a variável no eixo x aumenta, a variável no eixo y também aumenta. Os pontos estão agrupados, indicando uma forte relação.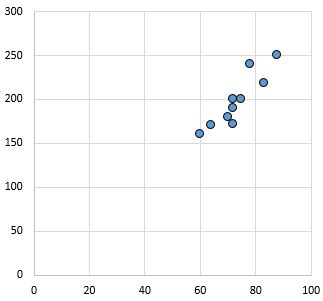

Coeficiente de correlação de Pearson: 0,94

Relação fraca e positiva: À medida que a variável no eixo x aumenta, a variável no eixo y também aumenta. Os pontos estão bastante dispersos, indicando uma relação fraca.

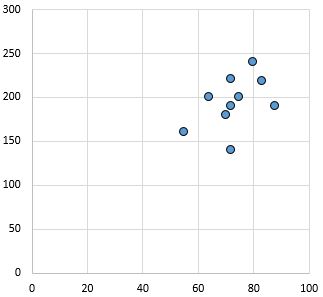
Coeficiente de correlação de Pearson: 0,44

Sem relação: Não existe uma relação clara (positiva ou negativa) entre as variáveis.

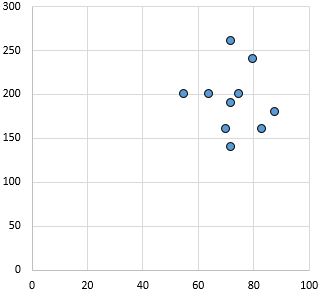
Coeficiente de correlação de Pearson: 0,03

Relação forte e negativa: à medida que a variável no eixo x aumenta, a variável no eixo y diminui. Os pontos estão bem agrupados, indicando um relacionamento forte.

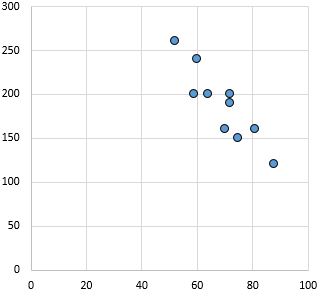
Coeficiente de correlação de Pearson: -0,87

Relacionamento fraco e negativo: À medida que a variável no eixo x aumenta, a variável no eixo y diminui. Os pontos estão bastante dispersos, indicando uma relação fraca.

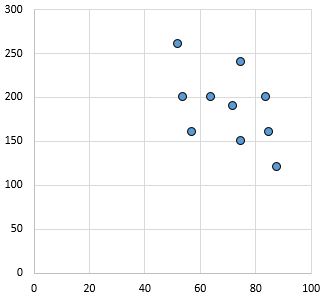
Coeficiente de correlação de Pearson: – 0,46

Testando a significância de um coeficiente de correlação de Pearson

Quando encontramos o coeficiente de correlação de Pearson para um conjunto de dados, muitas vezes estamos trabalhando com uma amostra de dados de uma população maior. Isto significa que é possível encontrar uma correlação diferente de zero para duas variáveis, mesmo que elas não estejam realmente correlacionadas na população geral.

Por exemplo, suponha que criemos um gráfico de dispersão para as variáveis X e Y para cada ponto de dados em toda a população e tenha a seguinte aparência:

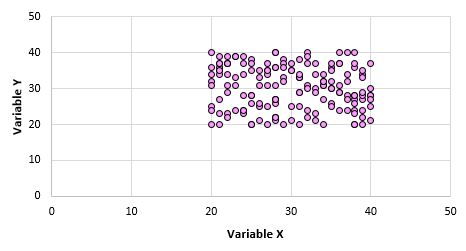
É óbvio que estas duas variáveis não estão correlacionadas. Porém, é possível que ao retirarmos uma amostra de 10 pontos da população, escolhamos os seguintes pontos:

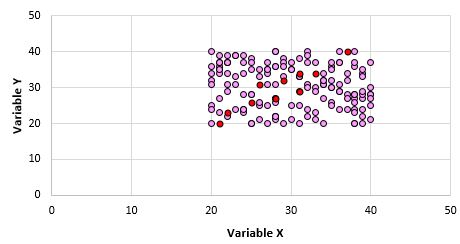
Podemos ver que o coeficiente de correlação de Pearson para esta amostra de pontos é 0,93, indicando uma forte correlação positiva mesmo que a correlação populacional seja zero.

Para testar se uma correlação entre duas variáveis é estatisticamente significativa ou não, podemos encontrar a seguinte estatística de teste:

Estatística de teste T = r * √ (n-2) / (1-r ² )

onde n é o número de pares em nossa amostra, r é o coeficiente de correlação de Pearson e a estatística do teste T segue uma distribuição com n-2 graus de liberdade.

Vamos revisar um exemplo de como testar a significância de um coeficiente de correlação de Pearson.

Exemplo

O conjunto de dados a seguir mostra a altura e o peso de 12 indivíduos:

O gráfico de dispersão abaixo mostra o valor dessas duas variáveis:

O coeficiente de correlação de Pearson para estas duas variáveis é r = 0,836.

A estatística de teste T = 0,836 * √ (12 -2) / (1-0,836 ² ) = 4,804.

De acordo com nossa calculadora de distribuição t , uma pontuação de 4,804 com 10 graus de liberdade tem um valor p de 0,0007. Como 0,0007 < 0,05, podemos concluir que a correlação entre peso e altura neste exemplo é estatisticamente significativa em alfa = 0,05.

Precauções

Embora um coeficiente de correlação de Pearson possa ser útil para nos dizer se duas variáveis têm ou não uma associação linear, precisamos ter três coisas em mente ao interpretar um coeficiente de correlação de Pearson:

1. Correlação não implica causalidade. Não é porque duas variáveis estão correlacionadas que uma necessariamente faz com que a outra apareça com maior ou menor frequência. Um exemplo clássico disso é a correlação positiva entre vendas de sorvete e ataques de tubarões. Quando as vendas de sorvetes aumentam em determinadas épocas do ano, os ataques de tubarões também tendem a aumentar.

Isso significa que comer sorvete causa ataques de tubarão? Claro que não! Isto significa simplesmente que no verão o consumo de gelo e os ataques de tubarões tendem a aumentar, porque o gelo é mais popular no verão e mais pessoas vão para o oceano durante o verão.

2. As correlações são sensíveis a valores discrepantes. Um valor discrepante extremo pode alterar significativamente o coeficiente de correlação de Pearson. Considere o exemplo abaixo:

As variáveis X e Y possuem coeficiente de correlação de Pearson de 0,00 . Mas imagine que temos um valor discrepante no conjunto de dados:

Contudo, o coeficiente de correlação de Pearson para estas duas variáveis é de 0,878 . Este outlier muda tudo. É por isso que, ao calcular a correlação para duas variáveis, é uma boa ideia visualizar as variáveis usando um gráfico de dispersão para verificar valores discrepantes.

3. Um coeficiente de correlação de Pearson não captura relações não lineares entre duas variáveis. Vamos imaginar que temos duas variáveis com a seguinte relação:

O coeficiente de correlação de Pearson para essas duas variáveis é 0,00 porque elas não possuem uma relação linear. No entanto, estas duas variáveis têm uma relação não linear: os valores de y são simplesmente os valores de x ao quadrado.

Ao usar o coeficiente de correlação de Pearson, lembre-se de que você está simplesmente testando se duas variáveis estão linearmente relacionadas. Mesmo que um coeficiente de correlação de Pearson nos diga que duas variáveis não estão correlacionadas, elas ainda poderão ter algum tipo de relação não linear. Esta é outra razão pela qual é útil criar um gráfico de dispersão ao analisar a relação entre duas variáveis: ele pode ajudar a detectar uma relação não linear.