Como usar fitdistr() em r para ajustar distribuições
Você pode usar a função fitdistr() do pacote MASS em R para estimar os parâmetros de uma distribuição maximizando a função de verossimilhança.
Esta função usa a seguinte sintaxe básica:
fitdistr(x, densofun,…)
Ouro:
- x : Um vetor numérico representando os valores da distribuição
- Densefun : a distribuição para estimar os parâmetros para
Observe que o argumento densofun aceita os seguintes nomes de distribuição potencial: beta , cauchy , qui-quadrado , exponencial , gama , geométrica , lognormal , logística , binomial negativo , normal , Poisson , t e Weibull .
O exemplo a seguir mostra como usar a função fitdistr() na prática.
Exemplo: como usar a função fitdistr() para ajustar distribuições em R
Suponha que usemos a função rnorm() em R para gerar um vetor de 200 valores que segue uma distribuição normal:
#make this example reproducible set. seeds (1) #generate sample of 200 observations that follows normal dist with mean=10 and sd=3 data <- rnorm(200, mean=10, sd=3) #view first 6 observations in sample head(data) [1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595
Podemos usar a função hist() para criar um histograma para visualizar a distribuição dos valores dos dados:
hist(data, col=' steelblue ')
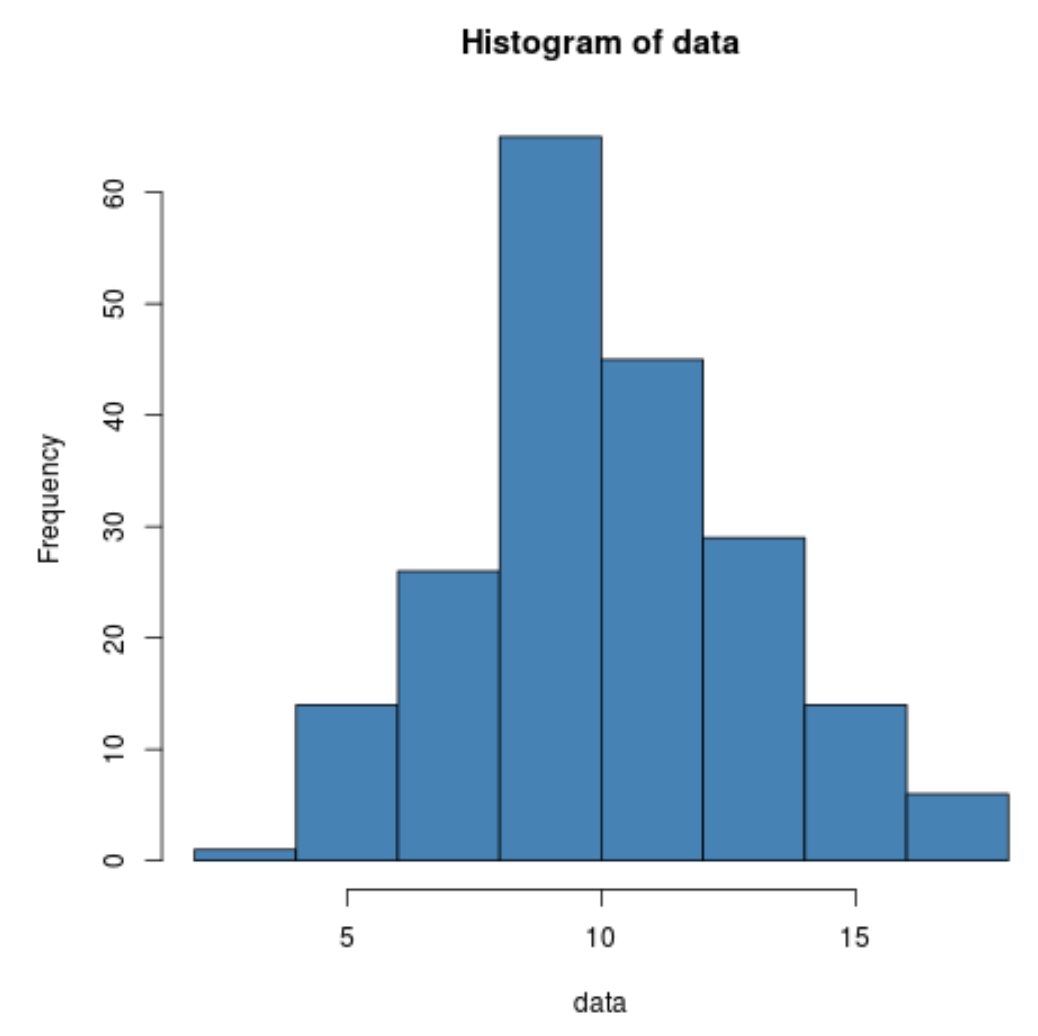
Podemos ver que os dados realmente parecem distribuídos normalmente.
Podemos então usar a função fitdistr() para estimar os parâmetros desta distribuição:
library (MASS)
#estimate parameters of distribution
fitdistr(data, “ normal ”)
mean sd
10.1066189 2.7803148
(0.1965979) (0.1390157)
A função fitdistr() estima que o vetor de valores segue uma distribuição normal com média de 10,1066189 e desvio padrão de 2,7803148 .
Esses valores não devem ser surpreendentes, pois geramos os dados usando a função rnorm() com valor médio de 10 e desvio padrão de 3.
Recursos adicionais
Os tutoriais a seguir explicam como realizar outras tarefas comuns em R:
Como traçar uma distribuição normal em R
Como gerar uma distribuição normal em R
Como realizar um teste de Shapiro-Wilk para normalidade em R