Como calcular assimetria e curtose no sas
Nas estatísticas, a assimetria e a curtose são duas maneiras de medir a forma de uma distribuição.
A assimetria mede a assimetria de uma distribuição.
- A assimetria negativa indica que a cauda está no lado esquerdo da distribuição.
- Uma inclinação positiva indica que a cauda está no lado direito da distribuição.
- Um valor zero indica que não há assimetria na distribuição, o que significa que a distribuição é perfeitamente simétrica.
A curtose mede se uma distribuição tem cauda pesada ou leve em comparação com uma distribuição normal .
- A curtose de uma distribuição normal é 0.
- Se uma determinada distribuição tiver uma curtose menor que 0, ela é considerada playkurtica , o que significa que tende a produzir menos valores discrepantes e menos extremos do que a distribuição normal.
- Se uma determinada distribuição tiver curtose superior a 0, diz-se que é leptocúrtica , o que significa que tende a produzir mais valores discrepantes do que a distribuição normal.
Para calcular assimetria e curtose de variáveis no SAS, você pode usar as instruções SKEWNESS e KURTOSIS em PROC MEANS .
O exemplo a seguir mostra como usar essas instruções na prática.
Exemplo: Calculando assimetria e curtose no SAS
Suponha que temos o seguinte conjunto de dados no SAS que contém informações sobre vários jogadores de basquete:
/*create dataset*/ data my_data; input team $points assists; datalines ; At 10 2 At 17 5 At 17 6 At 18 3 At 15 0 B 10 2 B 14 5 B 13 4 B 29 0 B 25 2 C 12 1 C 30 1 C 34 3 C 12 4 C 11 7 ; run ; /*view dataset*/ proc print data =my_data;
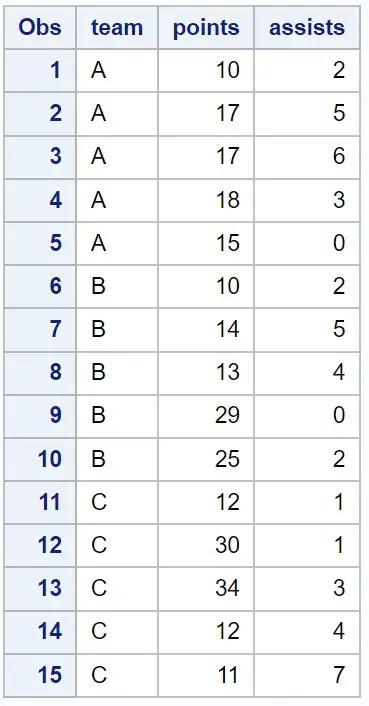
Podemos usar PROC MEANS com as instruções SKEWNESS e KURTOSIS para calcular a assimetria e a curtose de cada variável numérica no conjunto de dados:
/*calculate skewness and kurtosis for each numeric variable*/ proc means data =my_data SKEWNESS KURTOSIS ; run ;
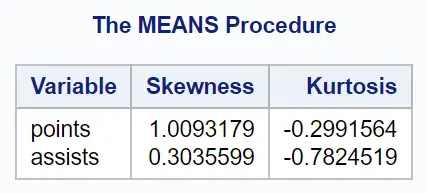
A tabela de saída exibe os valores de assimetria e curtose para cada variável numérica no conjunto de dados:
(1) pontos
- A variável points tem uma assimetria de 1,009 . Como esse valor é maior que 0, significa que a cauda está do lado direito da distribuição.
- A variável points tem uma curtose de -0,299 . Como esse valor é menor que 0, significa que a distribuição tem um pouco menos valores discrepantes e menos valores extremos do que a distribuição normal.
(2) ajuda
- A variável assistências tem uma assimetria de 0,304 . Como esse valor é maior que 0, significa que a cauda está do lado direito da distribuição.
- A variável suporte apresenta curtose de -0,782 . Como esse valor é menor que 0, significa que a distribuição tem menos valores discrepantes e menos valores extremos do que a distribuição normal.
Para visualizar a distribuição de valores para cada variável numérica no conjunto de dados, você pode usar PROC UNIVARIATE para criar histogramas para as variáveis de ponto e assistência:
/*create histograms for points and assists variables*/
proc univariate data =my_data;
var points assists;
histogram points assists;
run ;
Isso produz o seguinte histograma para a variável points :
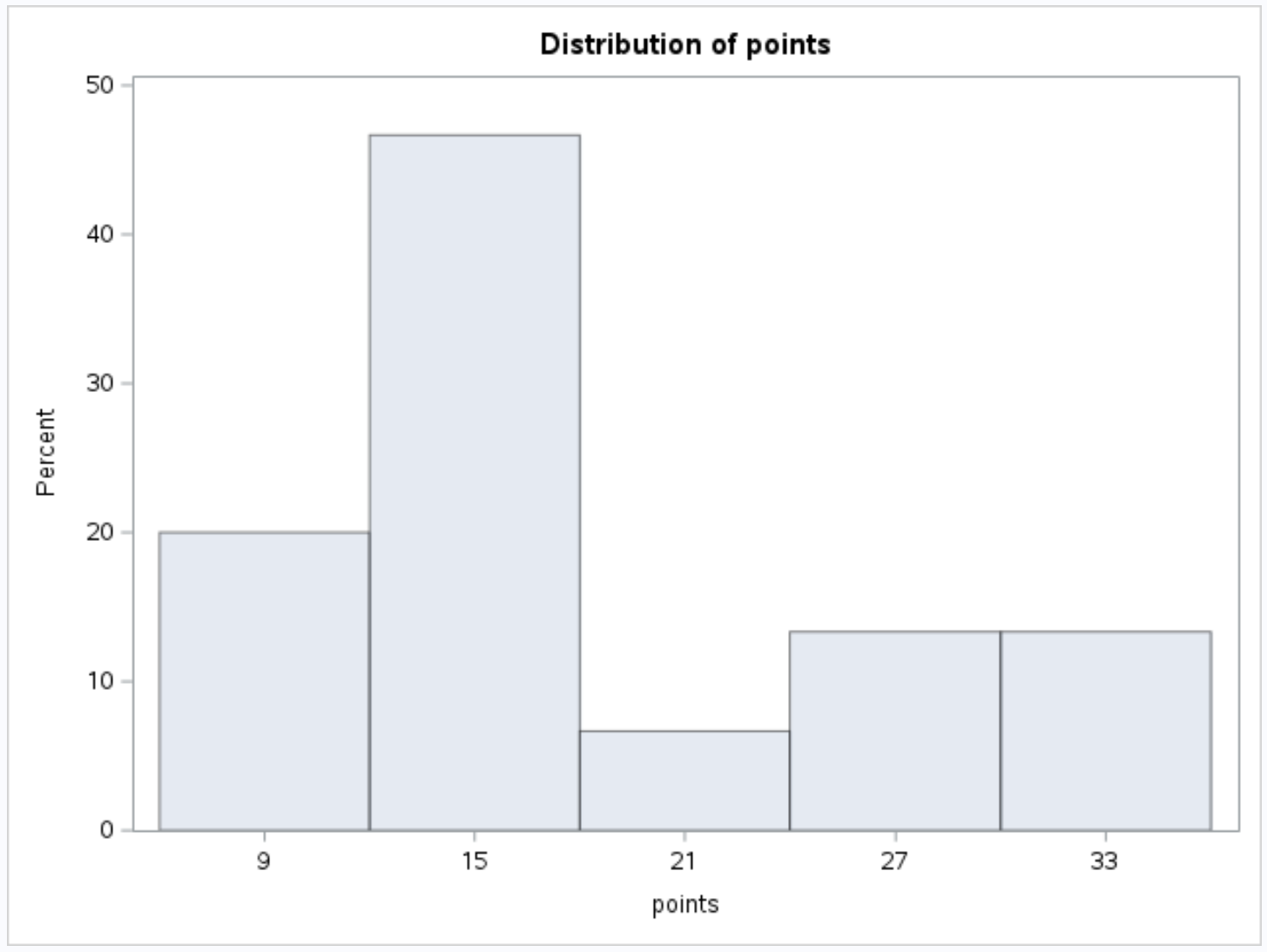
E o seguinte histograma para a variável assistencial :
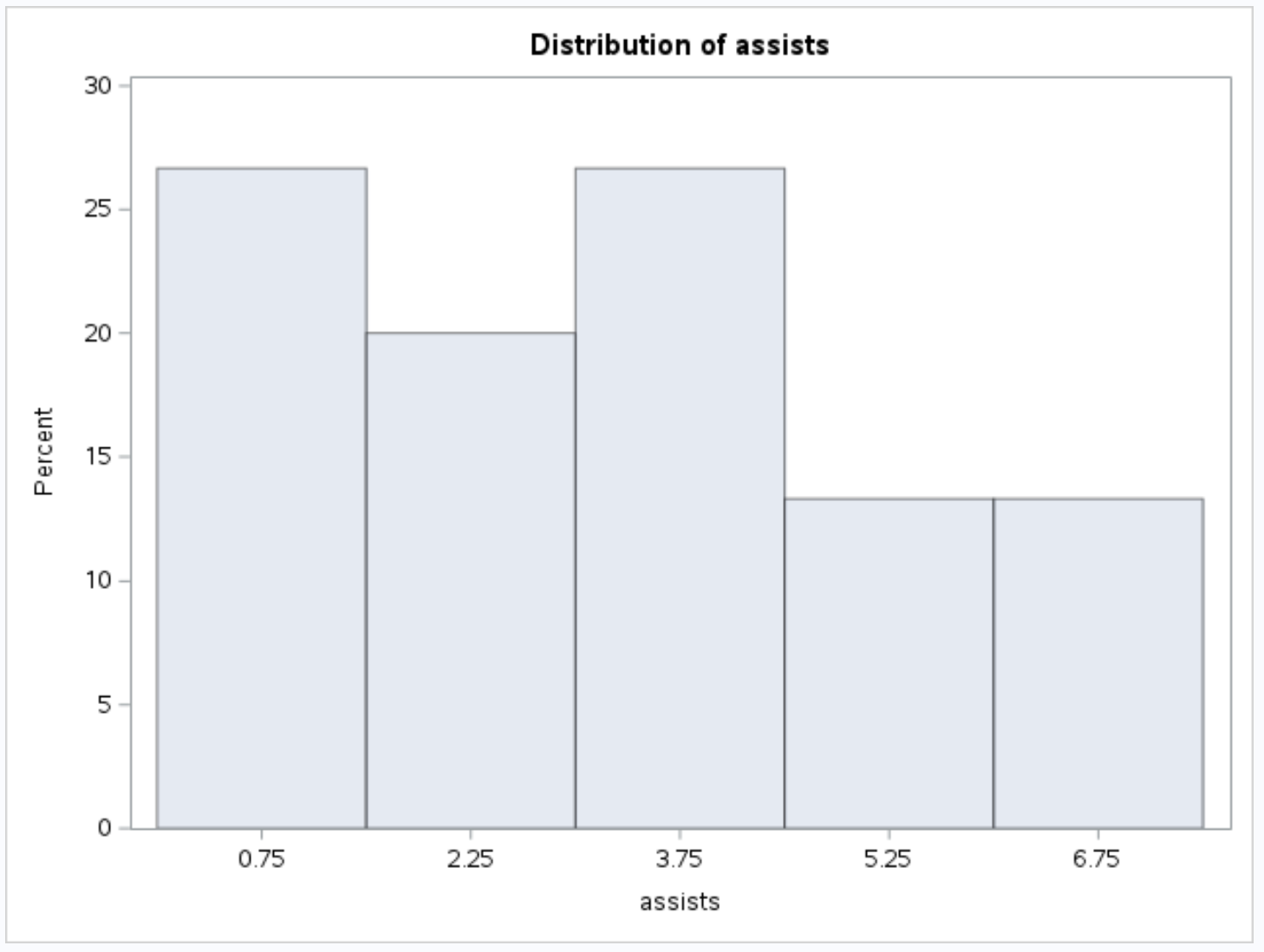
Recursos adicionais
Os tutoriais a seguir explicam como executar outras tarefas comuns no SAS:
Como calcular estatísticas descritivas no SAS
Como criar tabelas de frequência no SAS
Como calcular percentis no SAS
Como criar tabelas dinâmicas no SAS