Como calcular valores p no excel (3 exemplos)
Em estatística, usamos testes de hipóteses para determinar se uma afirmação sobre um parâmetro populacional é verdadeira ou não.
Quando realizamos um teste de hipótese, geralmente recebemos uma estatística de teste de pontuação T.
Depois de encontrar essa estatística de teste de pontuação t, podemos encontrar o valor p associado a ela.
Se este valor p for inferior a um determinado valor (por exemplo, 0,10, 0,05, 0,01), então rejeitamos a hipótese nula do teste e concluímos que os nossos resultados são estatisticamente significativos.
Os exemplos a seguir mostram como calcular um valor p para uma estatística de teste no Excel em três cenários diferentes.
Exemplo 1: Calcule o valor P para um teste bicaudal
Suponha que um botânico queira saber se a altura média de uma determinada espécie de planta é igual a 15 polegadas.
Em uma amostra aleatória de 12 plantas, ela descobre que a altura média da amostra é 14,33 polegadas e o desvio padrão da amostra é 1,37 polegadas.
Ele realiza um teste de hipótese usando as seguintes hipóteses nulas e alternativas:
H 0 (hipótese nula): μ= 15 polegadas
HA (hipótese alternativa): μ ≠ 15 polegadas
A estatística de teste é calculada da seguinte forma:
- t = ( X – µ) / (s/ √n )
- t = (14,33-15) / (1,37/√ 12 )
- t = -1,694
Os graus de liberdade associados a esta estatística de teste são n-1 = 12-1 = 11 .
Para encontrar o valor p para esta estatística de teste, usaremos a seguinte fórmula no Excel:
=T.DIST.2T(ABS(-1.694), 11)
A captura de tela a seguir mostra como usar esta fórmula na prática.
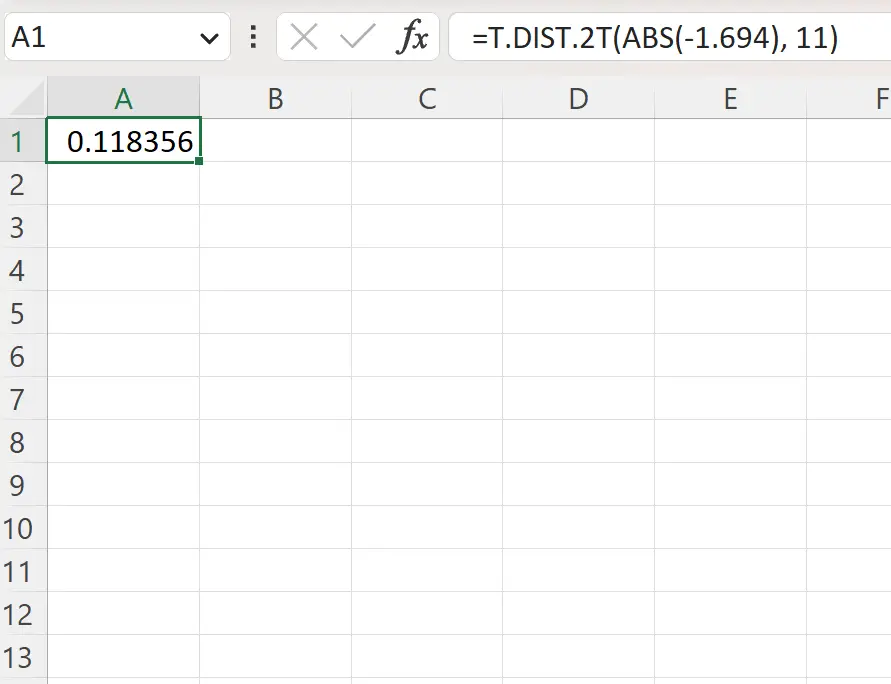
O valor p bicaudal é 0,1184 .
Já que esse valor não for inferior a 0,05, não rejeitamos a hipótese nula. Não temos evidências suficientes para dizer que a altura média das plantas seja diferente de 15 polegadas.
Exemplo 2: Calcule o valor P para o teste à esquerda
Suponha que assumamos que o peso médio de um determinado gadget produzido em uma fábrica seja de 20 gramas. No entanto, um inspetor estima que o peso médio real seja inferior a 20 gramas.
Para testar isso, ele pesa uma amostra aleatória simples de 20 widgets e obtém as seguintes informações:
- n = 20 widgets
- x = 19,8 gramas
- s = 3,1 gramas
Em seguida, realiza um teste de hipótese usando as seguintes hipóteses nulas e alternativas:
H 0 (hipótese nula): μ ≥ 20 gramas
HA (hipótese alternativa): μ < 20 gramas
A estatística de teste é calculada da seguinte forma:
- t = ( X – µ) / (s/ √n )
- t = (19,8-20) / (3,1/√ 20 )
- t = -0,2885
Os graus de liberdade associados a esta estatística de teste são n-1 = 20-1 = 19 .
Para encontrar o valor p para esta estatística de teste, usaremos a seguinte fórmula no Excel:
=T.DIST(-.2885, 19, TRUE)
A captura de tela a seguir mostra como usar esta fórmula na prática.
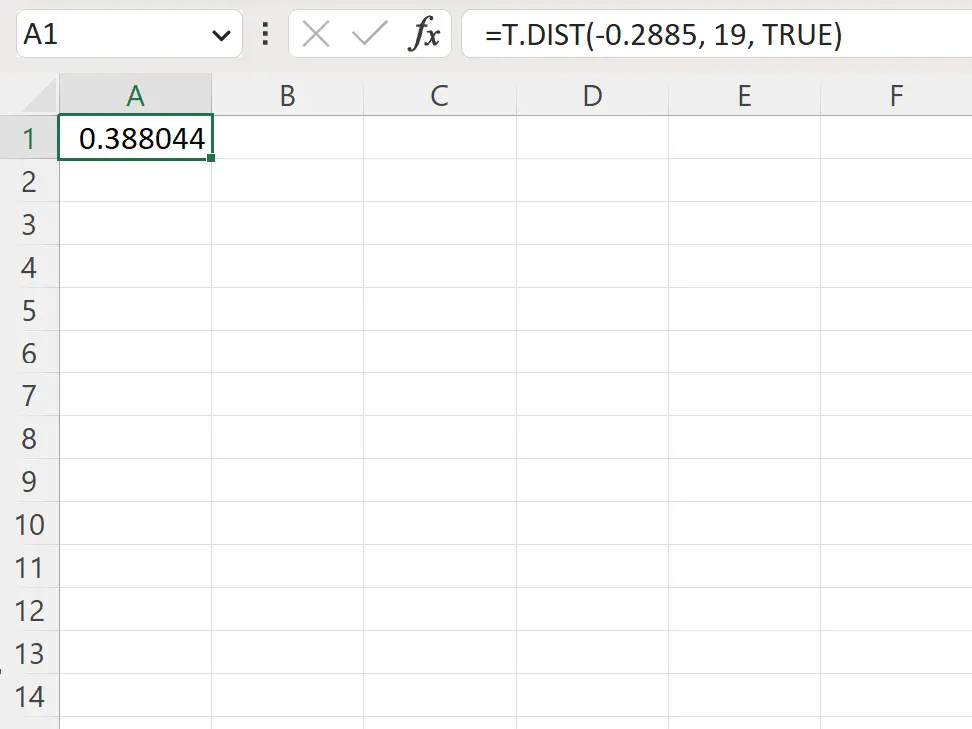
O valor p à esquerda é 0,388044 .
Já que esse valor não for inferior a 0,05, o inspetor não rejeita a hipótese nula. Não há evidências suficientes para afirmar que o peso médio real dos widgets produzidos nesta fábrica é inferior a 20 gramas.
Nota : Usamos o argumento TRUE para especificar que a função de distribuição cumulativa deve ser usada ao calcular o valor p.
Exemplo 3: Calcule o valor P para o teste de cauda direita
Vamos supor que a altura média de uma determinada espécie de planta seja de 25 centímetros. No entanto, um botânico diz que a verdadeira altura média é superior a 25 centímetros.
Para testar esta afirmação, ela mede a altura de uma amostra aleatória simples de 15 plantas e obtém as seguintes informações:
- n = 15 plantas
- x = 11,4 polegadas
- s = 2,5 polegadas
Em seguida, realiza um teste de hipótese usando as seguintes hipóteses nulas e alternativas:
H 0 (hipótese nula): μ ≤ 10 polegadas
HA (hipótese alternativa): μ > 10 polegadas
A estatística de teste é calculada da seguinte forma:
- t = ( X – µ) / (s/ √n )
- t = (11,4-10) / (2,5/√ 15 )
- t = 2,1689
Os graus de liberdade associados a esta estatística de teste são n-1 = 15-1 = 14 .
Para encontrar o valor p para esta estatística de teste, usaremos a seguinte fórmula no Excel:
=T.DIST.RT(2.1689, 14)
A captura de tela a seguir mostra como usar esta fórmula na prática.
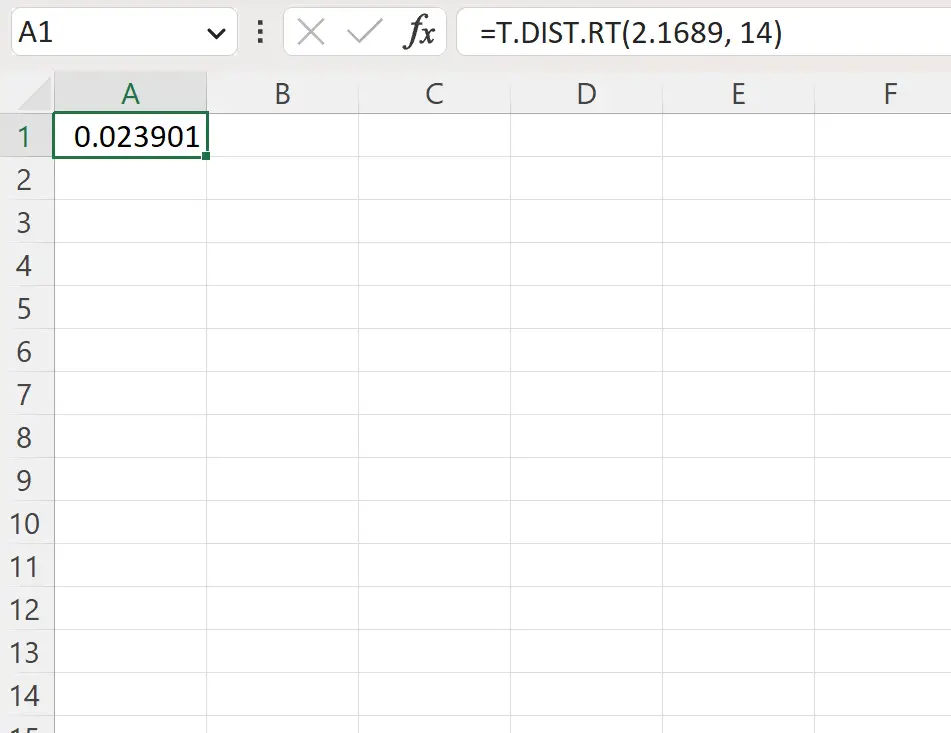
O valor p à direita é 0,023901 .
Sendo este valor inferior a 0,05, o botânico pode rejeitar a hipótese nula. Ela tem evidências suficientes para dizer que a verdadeira altura média desta espécie de planta é superior a 25 centímetros.
Recursos adicionais
Os tutoriais a seguir explicam como realizar outras tarefas comuns no Excel:
Como encontrar um valor P de uma pontuação Z no Excel
Como encontrar o valor P de uma estatística F no Excel
Como encontrar o valor P de uma estatística qui-quadrado no Excel