Como criar um intervalo de confiança usando a distribuição f

Para determinar se as variâncias de duas populações são iguais, podemos calcular a razão de variância σ ² ₁ / σ ² ₂ , onde σ ² ₁ é a variância da população 1 e σ ² ₂ é a variância da população 2.

Para estimar a verdadeira razão de variância populacional, geralmente pegamos uma amostra aleatória simples de cada população e calculamos a razão de variância amostral, s ₁ ² / s ₂ ² , onde s ₁ ² e s ₂ ² são as variâncias amostrais para a amostra 1 e a amostra . 2, respectivamente.

Este teste assume que s ₁ ² e s ₂ ² são calculados a partir de amostras independentes de tamanho n ₁ e n ₂ , ambas de populações normalmente distribuídas.

Quanto mais longe este rácio estiver de um, mais forte será a evidência de variações desiguais dentro da população.

O intervalo de confiança (1-α)100% para σ ² ₁ / σ ² ₂ é definido como:

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1, α/2}

onde F _{n 2 -1, n 1 -1, α/2} e F _{n 1 -1, n 2 -1, α/2}   são os valores críticos da distribuição F para o nível de significância α escolhido.

Os exemplos a seguir ilustram como criar um intervalo de confiança para σ ² ₁ / σ ² ₂ usando três métodos diferentes:

• Pela mão
• Utilize o Microsoft Excel
• Uso de software estatístico R

Para cada um dos exemplos a seguir, usaremos as seguintes informações:

• α = 0,05
• n ₁ = 16
• _n2 = 11
• s ₁ ² =28,2
• s ₂ ² = 19,3

Criando manualmente um intervalo de confiança

Para calcular manualmente um intervalo de confiança para σ ² ₁ / σ ² ₂ , simplesmente inseriremos os números que temos na fórmula do intervalo de confiança:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

Os únicos números que faltam são os valores críticos. Felizmente, podemos localizar esses valores críticos na tabela de distribuição F :

F _{n2-1, n1-1, α/2} = F _{10, 15, 0,025} = 3,0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0,025} = 1 / 3,5217 = 0,2839

(Clique para ampliar a tabela)

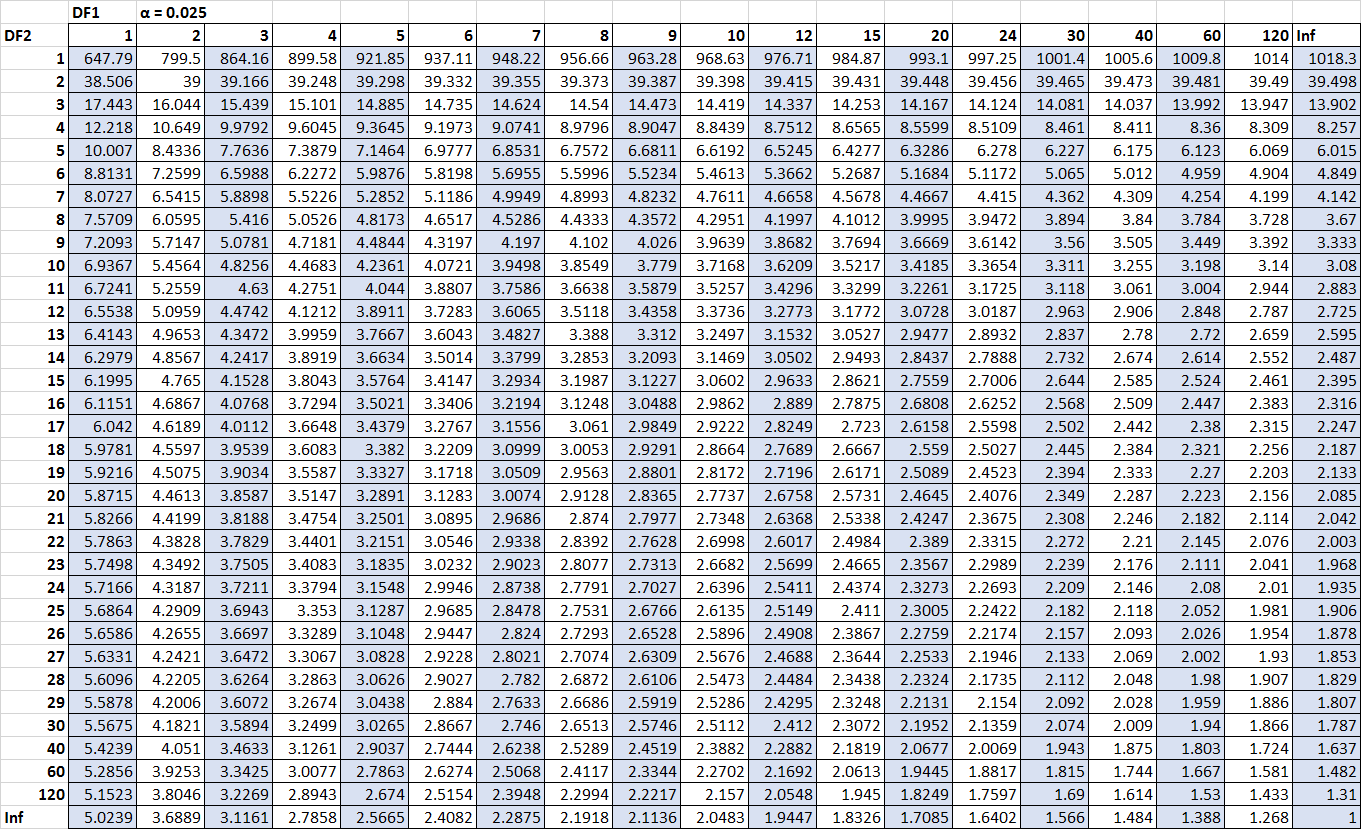
Agora podemos inserir todos os números no intervalo da fórmula de confiança:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

(28,2 / 19,3) * (0,2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28,2 / 19,3) * (3,0602)

0,4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4,4714

Assim, o intervalo de confiança de 95% para a razão das variâncias populacionais é (0,4148, 4,4714) .

Criando um intervalo de confiança usando Excel

A imagem a seguir mostra como calcular um intervalo de confiança de 95% para a razão de variância populacional no Excel. Os limites inferior e superior do intervalo de confiança são apresentados na coluna E e a fórmula utilizada para encontrar os limites inferior e superior é apresentada na coluna F:

Assim, o intervalo de confiança de 95% para a razão das variâncias populacionais é (0,4148, 4,4714) . Isso corresponde ao que obtivemos quando calculamos manualmente o intervalo de confiança.

Criando um intervalo de confiança usando R

O código a seguir ilustra como calcular um intervalo de confiança de 95% para a razão das variações populacionais em R:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

Assim, o intervalo de confiança de 95% para a razão das variâncias populacionais é (0,4148, 4,4714) . Isso corresponde ao que obtivemos quando calculamos manualmente o intervalo de confiança.

Recursos adicionais

Como ler o quadro de distribuição F
Como encontrar o valor crítico F no Excel