Tamanho do efeito: o que é e por que é importante
“A significância estatística é o que menos interessa nos resultados. É necessário descrever os resultados em termos de medidas de magnitude – não só um tratamento afecta as pessoas, mas também o quanto as afecta. -Gene V. Vidro
Nas estatísticas, costumamos usar valores p para determinar se há uma diferença estatisticamente significativa entre dois grupos.
Por exemplo, digamos que queremos saber se duas técnicas de estudo diferentes levam a resultados diferentes em testes. Portanto, temos um grupo de 20 alunos que utilizam uma técnica de estudo para se preparar para um teste, enquanto outro grupo de 20 alunos utiliza uma técnica de estudo diferente. Em seguida, aplicamos a cada aluno o mesmo teste.
Depois de executar um teste t de duas amostras para determinar uma diferença nas médias, descobrimos que o valor p do teste é 0,001. Se utilizarmos um nível de significância de 0,05, isso significa que existe uma diferença estatisticamente significativa entre as médias dos resultados dos dois grupos. Portanto, a técnica de estudo tem impacto nos resultados dos testes.
No entanto, embora o valor p nos diga que a técnica de estudo tem um impacto nos resultados dos testes, não nos diz a magnitude desse impacto. Para entender isso, precisamos saber o tamanho do efeito .
Qual é o tamanho do efeito?
Um tamanho de efeito é uma forma de quantificar a diferença entre dois grupos.
Embora um valor p possa nos dizer se há ou não uma diferença estatisticamente significativa entre dois grupos, um tamanho de efeito pode nos dizer quão grande é realmente essa diferença. Na prática, os tamanhos dos efeitos são muito mais interessantes e úteis de saber do que os valores-p.
Existem três maneiras de medir o tamanho do efeito, dependendo do tipo de análise que você está fazendo:
1. Diferença média padronizada
Quando você deseja estudar a diferença média entre dois grupos, a maneira apropriada de calcular o tamanho do efeito é usar uma diferença média padronizada . A fórmula mais popular para usar é conhecida como d de Cohen, que é calculada da seguinte forma:
D de Cohen = ( x1 – x2 )/ s
onde x 1 ex 2 são as médias amostrais do grupo 1 e do grupo 2, respectivamente, e s é o desvio padrão da população da qual os dois grupos foram sorteados.
Usando esta fórmula, o tamanho do efeito é fácil de interpretar:
- Um d de 1 indica que as médias dos dois grupos diferem em um desvio padrão.
- Um d de 2 significa que as médias do grupo diferem em dois desvios padrão.
- Um d de 2,5 indica que as duas médias diferem em 2,5 desvios padrão e assim por diante.
Outra forma de interpretar o tamanho do efeito é: um tamanho de efeito de 0,3 significa que a pontuação da pessoa média no Grupo 2 está 0,3 desvios padrão acima da média da pessoa do grupo 1 e, portanto, excede as pontuações de 62% das pessoas do grupo 1 . .
A tabela a seguir mostra diferentes tamanhos de efeito e seus percentis correspondentes:
| Tamanho do efeito | Porcentagem do grupo 2 que estaria abaixo da média das pessoas do grupo 1 |
|---|---|
| 0,0 | 50% |
| 0,2 | 58% |
| 0,4 | 66% |
| 0,6 | 73% |
| 0,8 | 79% |
| 1,0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1,8 | 96% |
| 2,0 | 98% |
| 2,5 | 99% |
| 3,0 | 99,9% |
Quanto maior o tamanho do efeito, maior será a diferença entre o indivíduo médio de cada grupo.
Em geral, um d de 0,2 ou menos é considerado um tamanho de efeito pequeno, um d de cerca de 0,5 é considerado um tamanho de efeito médio e um d de 0,8 ou maior é considerado um tamanho de efeito grande.
Assim, se as médias de dois grupos não diferirem em pelo menos 0,2 desvios padrão, a diferença é insignificante, mesmo que o valor p seja estatisticamente significativo.
2. Coeficiente de correlação
Quando se deseja estudar a relação quantitativa entre duas variáveis, a forma mais comum de calcular o tamanho do efeito é utilizar o coeficiente de correlação de Pearson . É uma medida de associação linear entre duas variáveis X e Y. Possui valor entre -1 e 1 onde:
- -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
- 0 indica nenhuma correlação linear entre duas variáveis
- 1 indica uma correlação linear perfeitamente positiva entre duas variáveis
A fórmula de cálculo do coeficiente de correlação de Pearson é bastante complexa, mas pode ser encontrada aqui para quem tiver interesse.
Quanto mais longe o coeficiente de correlação estiver de zero, mais forte será a relação linear entre duas variáveis. Isso também pode ser visto criando um gráfico de dispersão simples dos valores das variáveis X e Y.
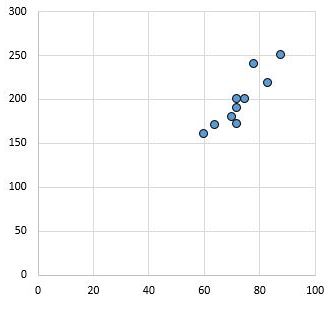
Por exemplo, o gráfico de dispersão a seguir mostra os valores de duas variáveis com um coeficiente de correlação de r = 0,94.
Este valor está longe de zero, indicando que existe uma forte relação positiva entre as duas variáveis.
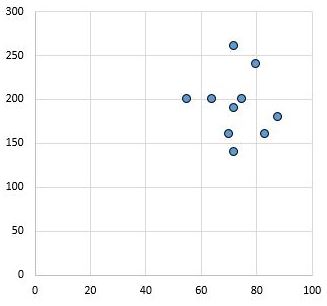
Por outro lado, o gráfico de dispersão a seguir mostra os valores de duas variáveis que possuem um coeficiente de correlação de r = 0,03. Este valor é próximo de zero, indicando que praticamente não existe relação entre as duas variáveis.
Em geral, o tamanho do efeito é considerado pequeno se o valor do coeficiente de correlação de Pearson r for cerca de 0,1, médio se r for cerca de 0,3 e grande se r for igual ou superior a 0,5.
3. Proporção de probabilidades
Quando você deseja estudar as chances de sucesso em um grupo de tratamento versus as chances de sucesso em um grupo de controle, a maneira mais comum de calcular o tamanho do efeito é usar a razão de chances .
Por exemplo, suponha que temos a seguinte tabela:
| Tamanho do efeito | #Sucesso | #Xadrez |
|---|---|---|
| Grupo de tratamento | TEM | B |
| Grupo de controle | VS | D |
A razão de chances seria calculada da seguinte forma:
Proporção de probabilidades = (AD) / (BC)
Quanto mais longe o odds ratio estiver de 1, maior será a probabilidade de o tratamento produzir um efeito real.
Os benefícios do uso de tamanhos de efeito em vez de valores P
Os tamanhos de efeito têm várias vantagens sobre os valores p:
1. O tamanho do efeito nos ajuda a ter uma ideia melhor de quão grande é a diferença entre dois grupos ou quão forte é a associação entre dois grupos. Um valor p só pode nos dizer se há ou não uma diferença significativa ou uma associação significativa.
2. Ao contrário dos valores p, os tamanhos dos efeitos podem ser usados para comparar quantitativamente os resultados de diferentes estudos realizados em diferentes ambientes. Por esse motivo, os tamanhos de efeito são frequentemente usados em meta-análises.
3. Os valores de P podem ser afetados por amostras grandes. Quanto maior o tamanho da amostra, maior o poder estatístico de um teste de hipótese, permitindo detectar até mesmo efeitos pequenos. Isto pode levar a valores de p baixos, apesar dos pequenos tamanhos de efeito que podem não ter significado prático.
Um exemplo simples pode ilustrar isso claramente: suponhamos que queremos saber se duas técnicas de estudo levam a resultados diferentes em testes. Temos um grupo de 20 alunos usando uma técnica de estudo enquanto outro grupo de 20 alunos usando uma técnica de estudo diferente. Em seguida, aplicamos a cada aluno o mesmo teste.
A pontuação média do grupo 1 é 90,65 e a pontuação média do grupo 2 é 90,75 . O desvio padrão para a amostra 1 é 2,77 e o desvio padrão para a amostra 2 é 2,78 .
Quando realizamos um teste t independente para duas amostras, verifica-se que a estatística do teste é -0,113 e o valor p correspondente é 0,91 . A diferença entre as pontuações médias dos testes não é estatisticamente significativa.
No entanto, considere se os tamanhos amostrais das duas amostras fossem ambos 200 , mas as médias e os desvios padrão permanecessem exatamente os mesmos.
Nesse caso, um teste t independente para duas amostras revelaria que a estatística do teste é -1,97 e o valor p correspondente está logo abaixo de 0,05 . A diferença entre as pontuações médias dos testes é estatisticamente significativa.
A razão subjacente pela qual amostras grandes podem levar a conclusões estatisticamente significativas é devido à fórmula usada para calcular as estatísticas do teste t :
estatística de teste t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Observe que quando n 1 e n 2 são pequenos, o denominador inteiro da estatística do teste t é pequeno. E quando você divide por um número pequeno, obtém um número grande. Isto significa que a estatística do teste t será grande e o valor p correspondente será pequeno, levando assim a resultados estatisticamente significativos.
O que é considerado um bom tamanho de efeito?
Uma pergunta que os alunos costumam fazer é: O que é considerado um bom tamanho de efeito?
A resposta curta: um tamanho de efeito não pode ser “bom” ou “ruim”, pois simplesmente mede o tamanho da diferença entre dois grupos ou a força da associação entre dois grupos.
No entanto, podemos usar as seguintes regras básicas para quantificar se a magnitude de um efeito é pequena, média ou grande:
D de Cohen:
- Um d de 0,2 ou menos é considerado um tamanho de efeito pequeno.
- Um d de 0,5 é considerado um tamanho de efeito médio.
- Um d de 0,8 ou superior é considerado um tamanho de efeito grande.
Coeficiente de Correlação de Pearson
- Um valor absoluto de r em torno de 0,1 é considerado um tamanho de efeito pequeno.
- Um valor absoluto de r em torno de 0,3 é considerado um tamanho de efeito médio.
- Um valor absoluto de r maior que 0,5 é considerado um tamanho de efeito grande.
No entanto, a definição de uma correlação “forte” pode variar de um campo para outro. Consulte este artigo para entender melhor o que é considerado uma forte correlação entre diferentes setores.