Como ler a tabela de distribuição do qui quadrado

Este tutorial explica como ler e interpretar o gráfico de distribuição qui-quadrado.

Qual é a tabela de distribuição do qui quadrado?

A tabela de distribuição Qui-quadrado é uma tabela que mostra os valores críticos da distribuição Qui-quadrado. Para usar a tabela de distribuição qui-quadrado, você só precisa saber dois valores:

• Graus de liberdade para o teste Qui-quadrado
• O nível alfa do teste (as opções comuns são 0,01, 0,05 e 0,10)

A imagem a seguir mostra as primeiras 20 linhas da tabela de distribuição qui-quadrado, com graus de liberdade no lado esquerdo da tabela e níveis alfa na parte superior da tabela:

Nota: Você pode encontrar uma tabela de distribuição qui-quadrado completa com mais graus de liberdade aqui.

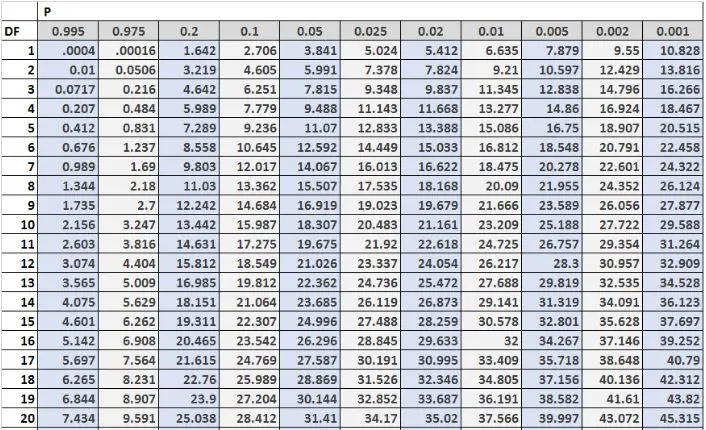
Os valores críticos na tabela são frequentemente comparados com as estatísticas de teste de um teste qui-quadrado. Se a estatística do teste for maior que o valor crítico encontrado na tabela, então você pode rejeitar a hipótese nula do teste Qui-quadrado e concluir que os resultados do teste são estatisticamente significativos.

Exemplos de uso da tabela de distribuição qui-quadrado

Mostraremos como usar a tabela de distribuição qui-quadrado com os três tipos de testes qui-quadrado a seguir:

• Teste qui-quadrado para independência
• Teste qui-quadrado para qualidade de ajuste
• Teste qui-quadrado para homogeneidade

Teste qui-quadrado para independência

Usamos um teste Qui-quadrado para independência quando queremos testar se existe ou não uma associação significativa entre duas variáveis categóricas.

Exemplo: Suponhamos que queremos saber se o género está ou não associado à preferência por um partido político. Pegamos uma amostra aleatória simples de 500 eleitores e perguntamos-lhes sobre suas preferências partidárias. Utilizando um nível de significância de 0,05, realizamos um teste qui-quadrado para determinar se o género está associado à preferência partidária. A tabela a seguir apresenta os resultados da pesquisa:

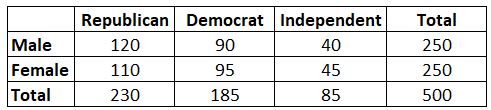
Acontece que a estatística de teste para este teste qui-quadrado é 0,864.

Então podemos encontrar o valor crítico do teste na tabela de distribuição do qui-quadrado. Os graus de liberdade são iguais a (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 e o problema nos disse que deveríamos usar um nível alfa de 0,05 Então, de acordo com a tabela de distribuição Qui-quadrado, o valor crítico do teste é 5,991 .

Como nossa estatística de teste é menor que nosso valor crítico, não conseguimos rejeitar a hipótese nula. Isto significa que não temos provas suficientes para afirmar que existe uma associação entre género e preferências partidárias.

Teste qui-quadrado para qualidade de ajuste

Usamos um teste de ajuste qui-quadrado quando queremos testar se uma variável categórica segue ou não uma distribuição hipotética.

Exemplo: O dono de uma loja diz que 30% de todos os seus clientes de fim de semana chegam na sexta-feira, 50% no sábado e 20% no domingo. Um pesquisador independente visita a loja em um fim de semana aleatório e encontra 91 clientes na sexta-feira, 104 no sábado e 65 no domingo. Usando um nível de significância de 0,10, realizamos um teste qui-quadrado para verificar a qualidade do ajuste e determinar se os dados são consistentes com a afirmação do proprietário da loja.

Neste caso, a estatística de teste é 10.616.

Então podemos encontrar o valor crítico do teste na tabela de distribuição do qui-quadrado. Os graus de liberdade são iguais a (#outcomes-1) = 3-1 = 2 e o problema nos diz que devemos usar um nível alfa de 0,10. Assim, de acordo com a tabela de distribuição Qui-quadrado, o valor crítico do teste é 4,605 .

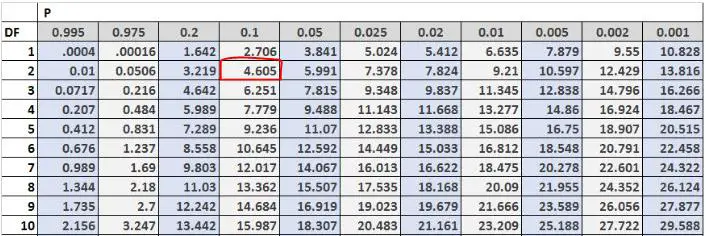
Como nossa estatística de teste é maior que nosso valor crítico, rejeitamos a hipótese nula. Isto significa que temos provas suficientes para afirmar que a verdadeira distribuição dos clientes que chegam a esta loja ao fim de semana não é igual a 30% na sexta-feira, 50% no sábado e 20% no domingo.

Teste qui-quadrado para homogeneidade

Usamos um teste qui-quadrado para homogeneidade quando queremos testar formalmente se há ou não diferença nas proporções entre vários grupos.

Exemplo: Um centro de treinamento de basquete quer ver se dois novos programas de treinamento melhoram a proporção de seus jogadores que passam em um teste de arremesso difícil. 172 jogadores são designados aleatoriamente para o programa 1, 173 para o programa 2 e 215 para o programa atual. Depois de usar os programas de treinamento por um mês, os jogadores fazem um teste de tiro. A tabela abaixo mostra a quantidade de jogadores que passaram no teste de tiro, com base no programa que utilizaram.

Utilizando um nível de significância de 0,05, realizamos um teste qui-quadrado para determinar se a taxa de sucesso é a mesma para cada programa de treinamento.

Acontece que a estatística de teste para este teste qui-quadrado é 4,208.

Então podemos encontrar o valor crítico do teste na tabela de distribuição do qui-quadrado. Os graus de liberdade são iguais a (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 e o problema nos disse que deveríamos usar um nível alfa de 0,05 Então, de acordo com a tabela de distribuição Qui-quadrado, o valor crítico do teste é 5,991 .

Como nossa estatística de teste é menor que nosso valor crítico, não conseguimos rejeitar a hipótese nula. Isto significa que não temos provas suficientes para afirmar que os três programas de formação produzem resultados diferentes.