Como calcular manualmente um valor p de um teste t
Um dos testes mais comumente usados em estatística é o teste t , que é frequentemente usado para determinar se a média de uma população é igual a um determinado valor.
Por exemplo, digamos que queremos saber se a altura média de uma determinada espécie de planta é igual a 15 polegadas. Para testar isso, poderíamos coletar uma amostra aleatória de 20 plantas, encontrar a média amostral e o desvio padrão amostral e realizar um teste t para determinar se a altura média é realmente de 15 polegadas.
As hipóteses nula e alternativa do teste são as seguintes:
H 0 : µ = 15
Ha : µ ≠ 15
A fórmula para a estatística de teste é:
t = ( X -μ) / (s/ √n )
onde x é a média amostral, μ é a média hipotética (em nosso exemplo seria 15), s é o desvio padrão amostral e n é o tamanho da amostra.
Depois de sabermos o valor de t , podemos usar um software estatístico ou uma calculadora online para encontrar o valor p correspondente. Se o valor p estiver abaixo de um determinado nível alfa (as escolhas comuns são 0,01, 0,05 e 0,10), então podemos rejeitar a hipótese nula e concluir que a altura média da planta não é igual a 15 polegadas.
No entanto, também é possível estimar manualmente o valor p do teste usando uma tabela de distribuição t . Neste artigo explicaremos como fazer isso.
Exemplo: cálculo manual do valor p de um teste t
Problema : Bob quer saber se a altura média de uma determinada espécie de planta é igual a 15 polegadas. Para testar isso, ele coleta uma amostra aleatória de 20 plantas e descobre que a média amostral é de 14 polegadas e o desvio padrão da amostra é de 3 polegadas. Execute um teste t usando um nível alfa de 0,05 para determinar se a verdadeira altura média da população é na verdade 15 polegadas.
Solução:
Passo 1: Indique as hipóteses nula e alternativa.
H 0 : µ = 15
Ha : µ ≠ 15
Etapa 2: Encontre a estatística de teste.
t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1,49
Etapa 3: Encontre o valor p para a estatística de teste.
Para encontrar o valor p manualmente, precisamos usar a tabela de distribuição t com n-1 graus de liberdade. Em nosso exemplo, nosso tamanho de amostra é n = 20, então n-1 = 19.
Na tabela de distribuição t abaixo, precisamos olhar para a linha que corresponde a “19” no lado esquerdo e tentar encontrar o valor absoluto da nossa estatística de teste 1,49 .
Observe que 1,49 não aparece na tabela, mas fica entre os dois valores 1,328 e 1,729 .
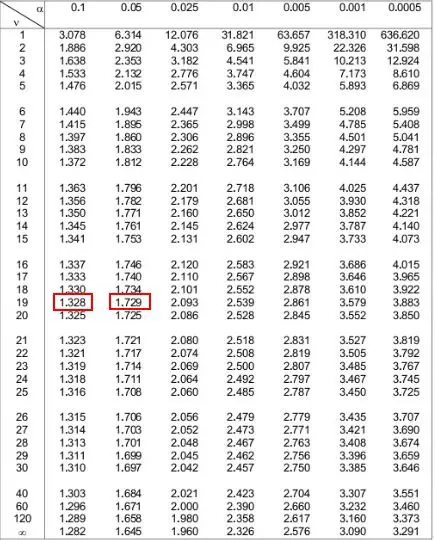
Depois podemos observar os dois níveis alfa no topo da tabela que correspondem a estes dois números. Vemos que eles são 0,1 e 0,05 .
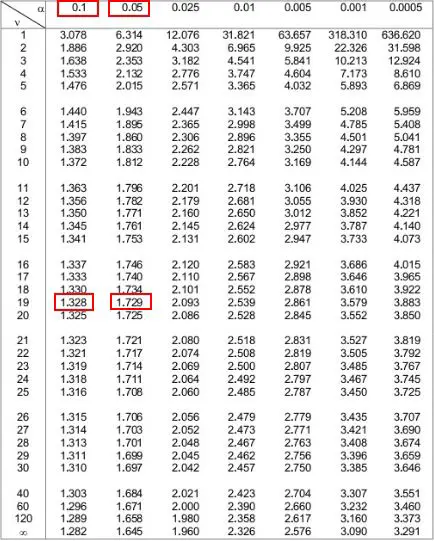
Isso significa que o valor p para um teste unilateral está entre 0,1 e 0,05. Vamos chamá-lo de 0,075. Como nosso teste t é bicaudal, precisamos multiplicar esse valor por 2. Portanto, nosso valor p estimado é 0,075 * 2 = 0,15 .
Etapa 4: tire uma conclusão.
Como este valor p não é inferior ao nível alfa escolhido de 0,05, não podemos rejeitar a hipótese nula. Assim, não temos evidências suficientes para dizer que a verdadeira altura média desta espécie de planta seja diferente de 15 polegadas.
Verifique os resultados com uma calculadora
Podemos inserir nossa estatística de teste t e graus de liberdade em uma calculadora de valor p on-line para ver o quão próximo nosso valor p estimado estava do valor p verdadeiro:

O verdadeiro valor p é 0,15264 , que é muito próximo do nosso valor p estimado de 0,15 .
Conclusão
Vimos neste artigo que é possível estimar manualmente o valor p de um teste t usando a tabela de distribuição t. No entanto, na maioria dos cenários, você nunca terá que calcular o valor p manualmente e poderá usar um software estatístico como R e Excel ou uma calculadora online para encontrar o valor p exato do teste.
Na maioria dos casos, especialmente em estudos e experimentos estatísticos rigorosos, você desejará usar uma calculadora para encontrar o valor p exato de um teste t para ser o mais preciso possível, mas é bom saber que você sempre pode estimar manualmente o Valor p de um teste t, se for absolutamente necessário.