Socs: um acrônimo útil para descrever distribuições

Nas estatísticas, muitas vezes queremos compreender como um conjunto de dados é distribuído. Em particular, há quatro coisas que é útil saber sobre uma distribuição:

1 . Forma

• A distribuição é simétrica ou distorcida para um lado?
• A distribuição é unimodal (um pico) oubimodal (dois picos)?

2. Valores discrepantes

• Há algum outlier presente na distribuição?

3. Centro

• Qual é a média, mediana e modo de distribuição?

4. Espalhar

• Quais são o intervalo, intervalo interquartil, desvio padrão e variância da distribuição?

SOCS é um acrônimo útil que podemos usar para lembrar essas quatro coisas. Significa “forma, outliers, centro, propagação”.

Vejamos um exemplo simples de como usar SOCS para descrever uma distribuição.

Exemplo: como usar SOCS para descrever uma distribuição

Digamos que temos o seguinte conjunto de dados que mostra a altura de uma amostra de 20 plantas diferentes.

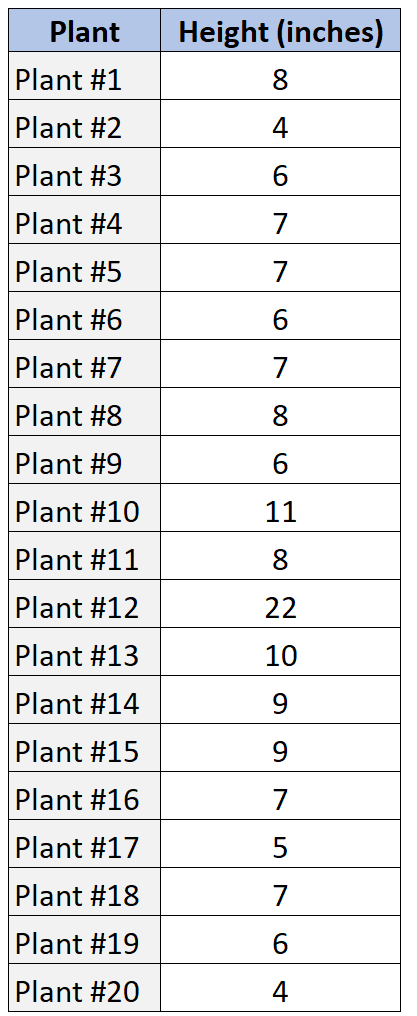
Veja como podemos usar o SOCS para descrever essa distribuição de valores de dados.

Forma

Primeiro, queremos descrever a forma da distribuição.

Uma forma útil de visualizar a forma da distribuição é criar um histograma, que exibe as frequências de cada valor no conjunto de dados:

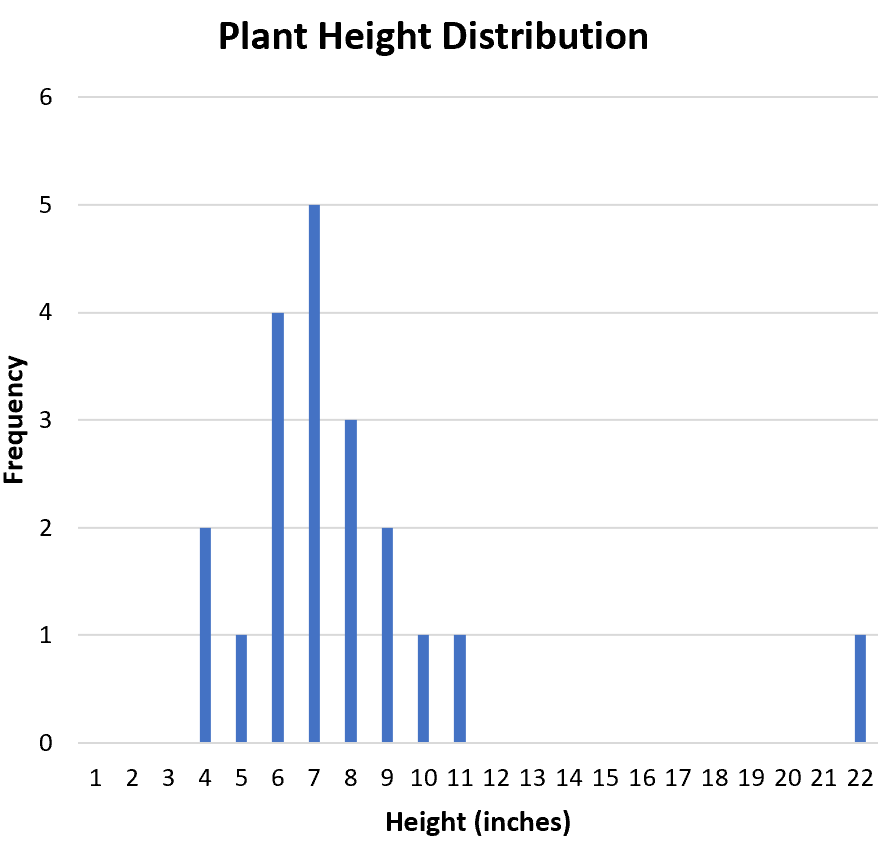
A distribuição é simétrica ou distorcida para um lado?   No histograma podemos ver que a distribuição é aproximadamente simétrica. Em outras palavras, os valores não são tendenciosos para um lado ou para outro.

A distribuição é unimodal (um pico) ou bimodal (dois picos)? A distribuição é unimodal. Tem um pico no valor “7”.

Valores discrepantes

A seguir, queremos determinar se há algum outlier no conjunto de dados. A partir do histograma podemos inspecionar visualmente a distribuição e ver que 22 é potencialmente um valor discrepante:

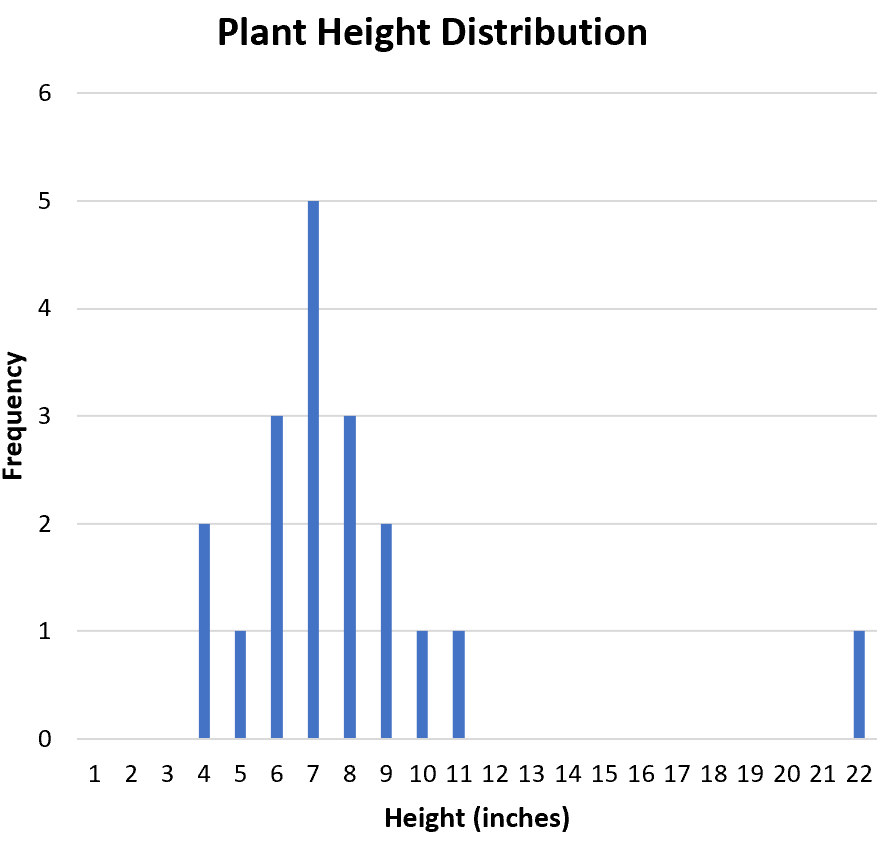
Uma forma comum de definir formalmente um valor discrepante é qualquer valor que seja 1,5 vezes o intervalo interquartil acima do terceiro quartil ou abaixo do primeiro quartil.

Usando a calculadora de intervalo interquartil, podemos inserir os 20 valores de dados brutos e ver que o terceiro quartil é 9 , o intervalo interquartil é 3 e, portanto, qualquer valor maior que 9 + (1,5*3) = 13,5 é um valor discrepante, por definição.

Como 22 é maior que 13,5, podemos declarar 22 como um valor discrepante.

Centro

Queremos então descrever onde está localizado o centro da distribuição. Três medidas comuns de tendência central que podemos usar são a média, a mediana e a moda.

Média: Este é o valor médio da distribuição. Descobrimos isso somando todos os valores individuais e depois dividindo pelo número total de valores:

Média = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85

Mediana: Este é o valor “médio” da distribuição. Descobrimos isso ordenando todos os valores do menor para o maior e depois identificando o valor mediano. Acontece que são 7 .

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

Moda: Este é o valor que aparece com mais frequência. Acontece que são 7 .

Espalhar

A seguir, queremos descrever a distribuição de valores na distribuição. Quatro medidas comuns de dispersão que podemos usar são intervalo, intervalo interquarílico, desvio padrão e variância.

Faixa: Esta é a diferença entre o maior e o menor valor no conjunto de dados. Isso resulta em 22 – 4 = 18 .

Intervalo interquartil: mede a largura dos 50% intermediários dos valores dos dados. Inserindo os 20 valores de dados brutos na calculadora do intervalo interquartil, podemos ver que isso é igual a 3 .

Desvio padrão: Esta é uma medida da distribuição média dos valores dos dados. Inserindo os 20 valores de dados brutos na calculadora de variância e desvio padrão, podemos ver que o desvio padrão é igual a 3,69 .

Variância: Este é simplesmente o desvio padrão, ao quadrado. Isso é igual a 3,69 ² = 13,63 .

Conclusão

Usando o SOCS como guia, conseguimos descrever a distribuição da altura das plantas da seguinte forma:

• A distribuição era unimodal e simétrica, ou seja, tinha apenas um pico e não era distorcida para um lado ou para outro.
• A distribuição tinha um outlier: 22.
• A distribuição teve média de 7,85, mediana de 7 e moda de 7.
• A distribuição teve intervalo de 18, intervalo interquartil de 3, desvio padrão de 3,69 e variância de 13,63.

Observe que podemos usar SOCS para descrever qualquer distribuição, o que é uma forma útil para entendermos completamente a forma de uma distribuição, se ela tem outliers, onde está aproximadamente o centro e como distribuir os valores dos dados. são.