Como calcular o erro quadrático médio (rmse) no excel
Em estatística, a análise de regressão é uma técnica que usamos para compreender a relação entre uma variável preditora, x, e uma variável de resposta, y.
Quando realizamos análise de regressão, obtemos um modelo que nos informa o valor previsto da variável resposta com base no valor da variável preditora.
Uma maneira de avaliar quão bem nosso modelo se ajusta a um determinado conjunto de dados é calcular o erro quadrático médio , que é uma métrica que nos diz a que distância nossos valores previstos estão de nossos valores observados, em média.
A fórmula para encontrar o erro quadrático médio, mais comumente conhecido como RMSE , é:
RMSE = √[ Σ(P i – O i ) 2 / n ]
Ouro:
- Σ é um símbolo sofisticado que significa “soma”
- Pi é o valor previsto para a i-ésima observação no conjunto de dados
- O i é o valor observado para a i-ésima observação no conjunto de dados
- n é o tamanho da amostra
Notas técnicas :
- O erro quadrático médio pode ser calculado para qualquer tipo de modelo que produza valores previstos, que podem então ser comparados aos valores observados de um conjunto de dados.
- O erro quadrático médio também é às vezes chamado de desvio quadrático médio, que geralmente é abreviado como RMSD.
A seguir, vejamos um exemplo de como calcular o erro quadrático médio no Excel.
Como calcular o erro quadrático médio no Excel
Não existe uma função integrada para calcular o RMSE no Excel, mas podemos calculá-lo facilmente com uma única fórmula. Mostraremos como calcular o RMSE para dois cenários diferentes.
Cenário 1
Em um cenário, você pode ter uma coluna contendo os valores previstos do seu modelo e outra coluna contendo os valores observados. A imagem abaixo mostra um exemplo deste cenário:
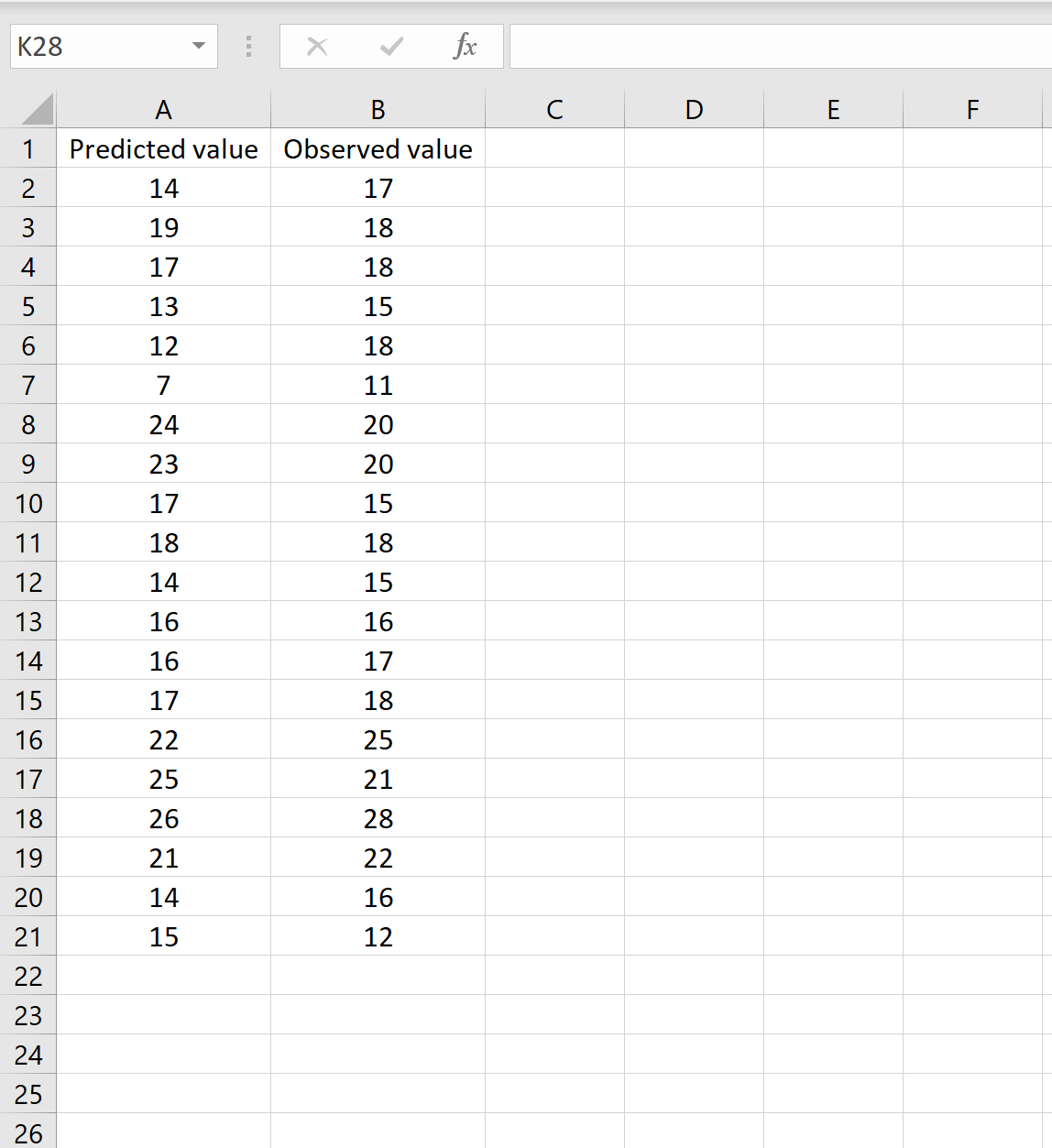
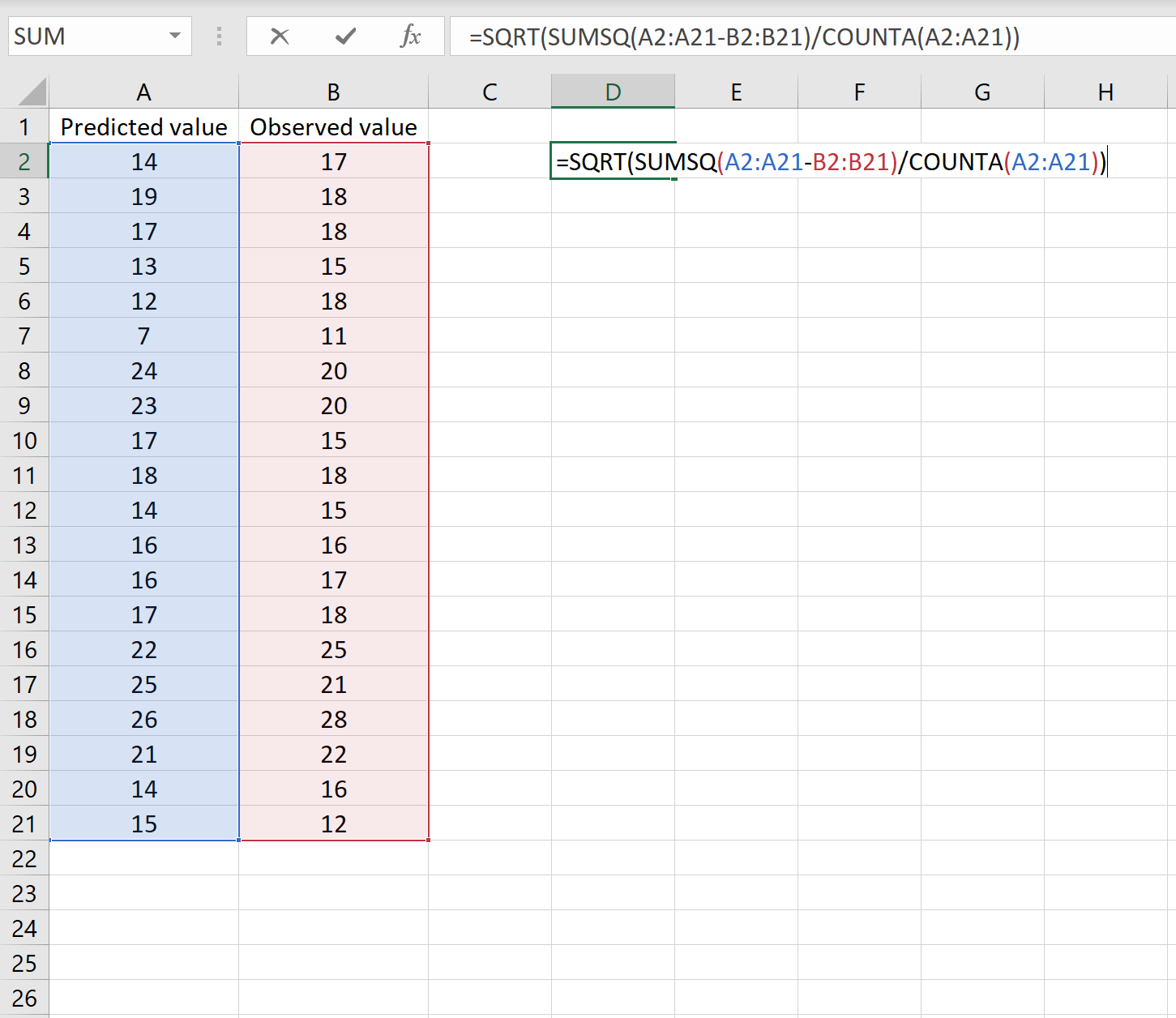
Nesse caso, você pode calcular o RMSE digitando a seguinte fórmula em qualquer célula e clicando em CTRL+SHIFT+ENTER:
=QUADRADO(SOMAQ(A2:A21-B2:B21) / CONTAGEM(A2:A21))
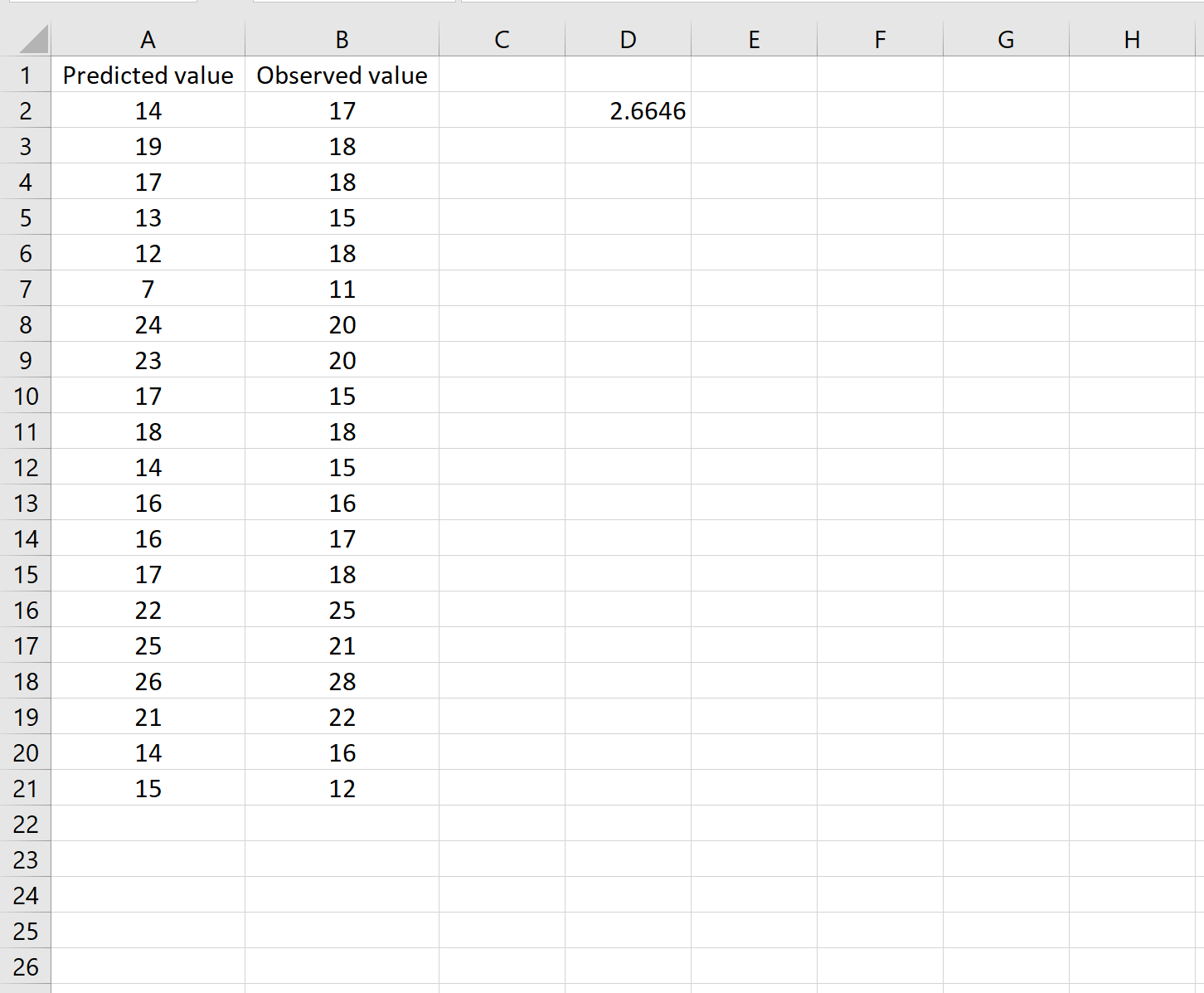
Isso nos diz que o erro quadrático médio é 2,6646 .
A fórmula pode parecer um pouco complicada, mas faz sentido quando você a decompõe:
= QUADRADO( SOMAQ(A2:A21-B2:B21) / CONTAGEM(A2:A21) )
- Primeiro, calculamos a soma dos quadrados das diferenças entre os valores previstos e observados usando a função SUMSQ() .
- A seguir, dividimos pelo tamanho da amostra do conjunto de dados usando COUNTA() , que conta o número de células em um intervalo que não está vazio.
- Finalmente, extraímos a raiz quadrada de todo o cálculo usando a função SQRT() .
Cenário 2
Em outro cenário, você já pode ter calculado as diferenças entre os valores previstos e observados. Neste caso você terá apenas uma coluna mostrando as diferenças.
A imagem abaixo mostra um exemplo desse cenário. Os valores previstos são mostrados na coluna A, os valores observados na coluna B e a diferença entre os valores previstos e observados na coluna D:
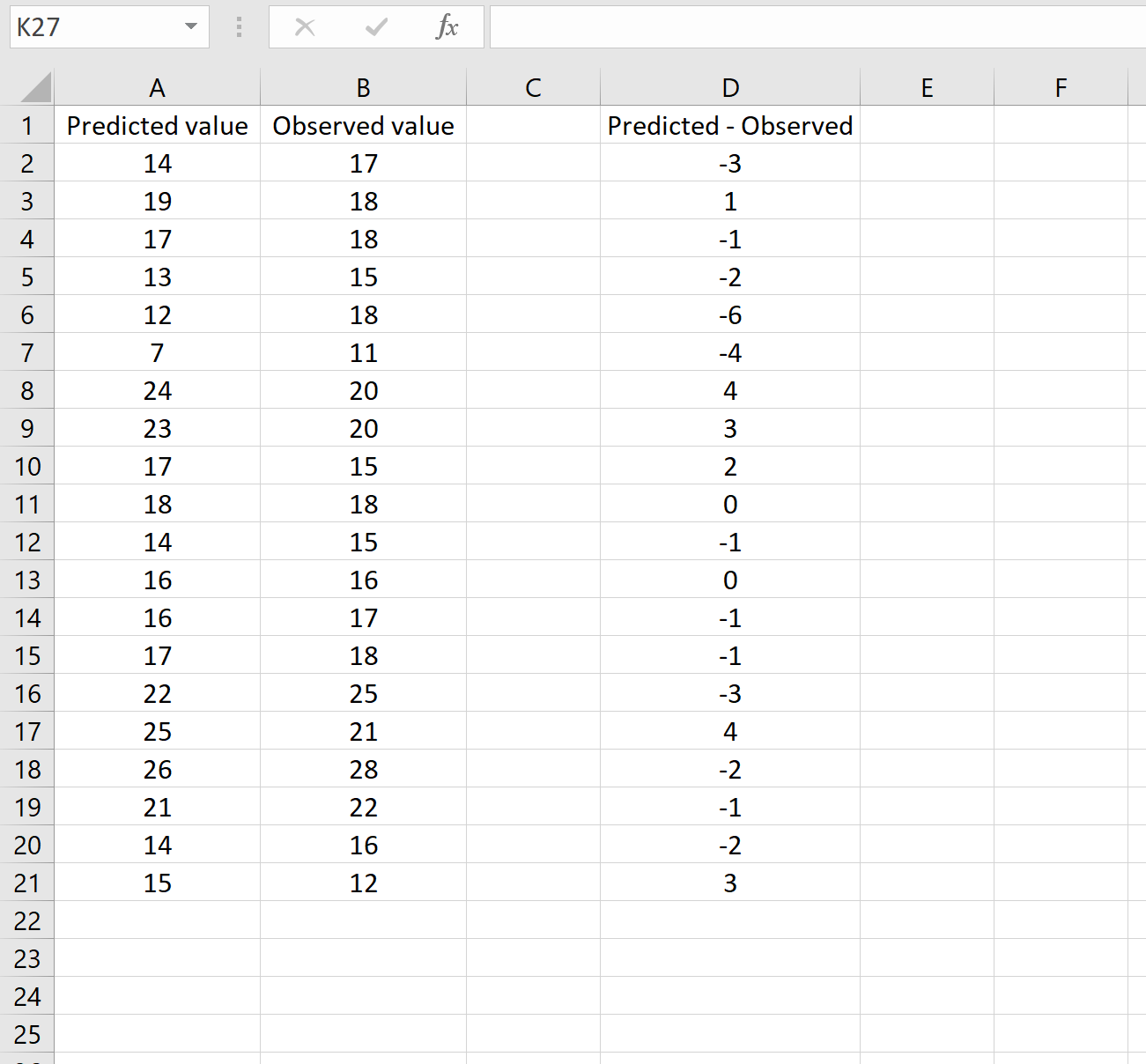
Nesse caso, você pode calcular o RMSE digitando a seguinte fórmula em qualquer célula e clicando em CTRL+SHIFT+ENTER:
=QUADRADO(SOMAQ(D2:D21) / CONTAGEM(D2:D21))
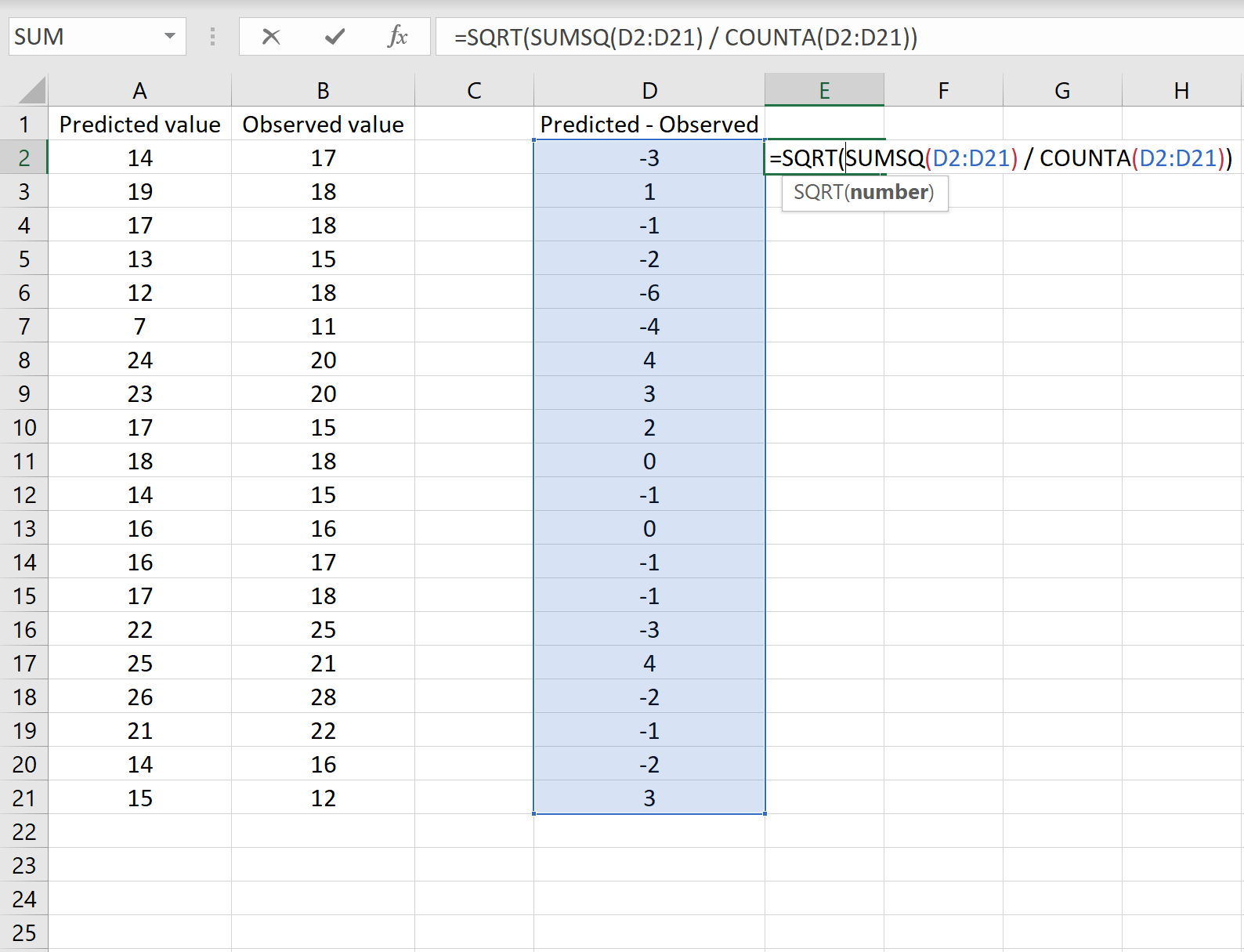
Isto diz-nos que o erro quadrático médio é 2,6646 , o que corresponde ao resultado obtido no primeiro cenário. Isto confirma que estas duas abordagens para calcular o RMSE são equivalentes.
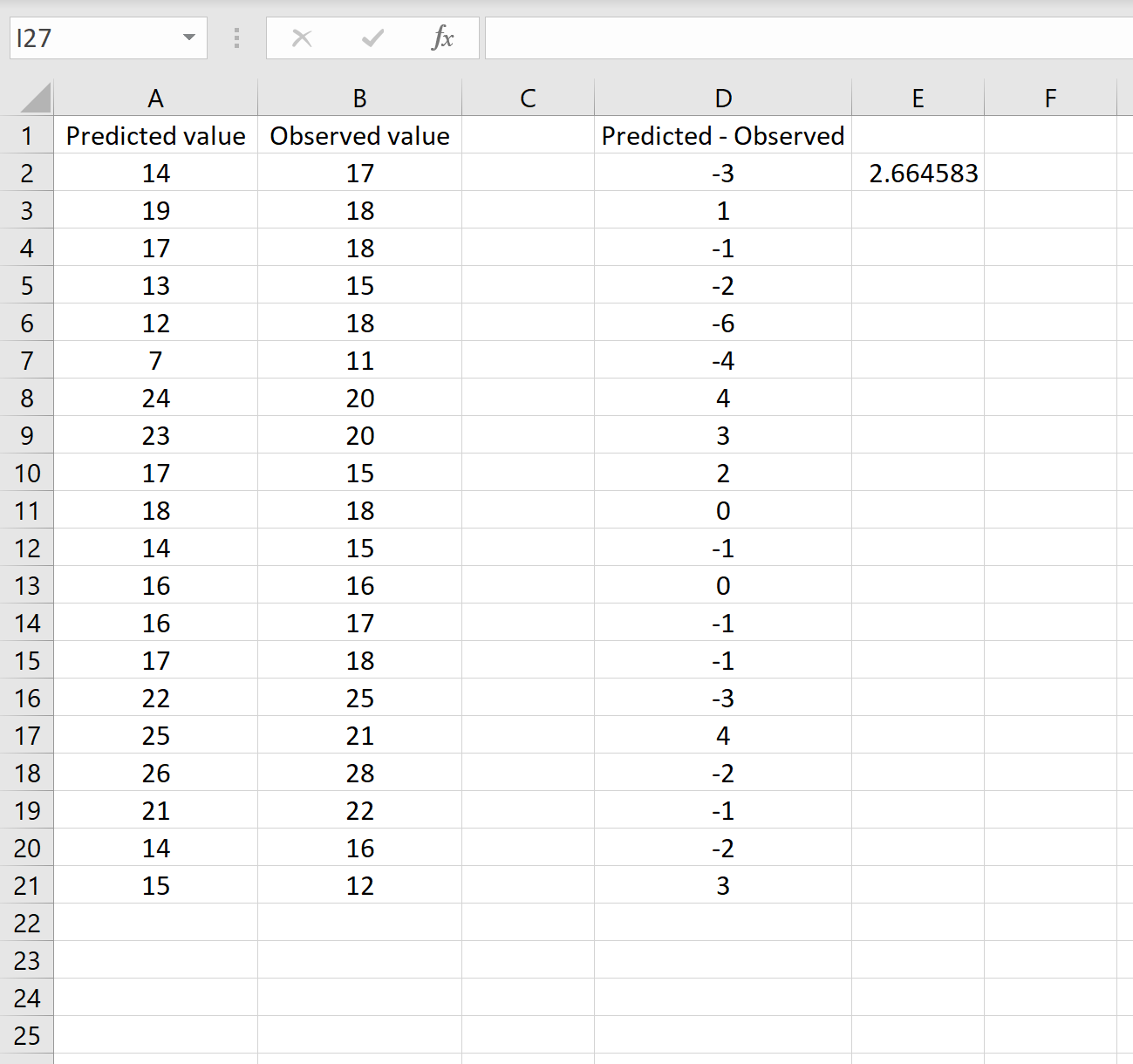
A fórmula que usamos neste cenário é apenas ligeiramente diferente daquela que usamos no cenário anterior:
= QUADRADO( SOMAQ(D2:D21) / CONTAGEM(D2:D21) )
- Como já calculamos as diferenças entre os valores previstos e observados na coluna D, podemos calcular a soma das diferenças quadradas usando a função SUMSQ(). função apenas com os valores da coluna D.
- A seguir, dividimos pelo tamanho da amostra do conjunto de dados usando COUNTA() , que conta o número de células em um intervalo que não está vazio.
- Finalmente, extraímos a raiz quadrada de todo o cálculo usando a função SQRT() .
Como interpretar o RMSE
Conforme mencionado anteriormente, o RMSE é uma maneira útil de ver até que ponto um modelo de regressão (ou qualquer modelo que produza valores previstos) é capaz de “ajustar-se” a um conjunto de dados.
Quanto maior o RMSE, maior a diferença entre os valores previstos e observados, ou seja, pior o modelo de regressão se ajusta aos dados. Por outro lado, quanto menor o RMSE, melhor o modelo é capaz de ajustar os dados.
Pode ser particularmente útil comparar o RMSE de dois modelos diferentes para ver qual modelo melhor se ajusta aos dados.
Para obter mais tutoriais no Excel, não deixe de conferir nossa página Guias do Excel , que lista todos os tutoriais do Excel sobre estatísticas.