Como realizar um teste t de duas amostras no excel

Um teste t de duas amostras é usado para testar se as médias de duas populações são iguais ou não.

Este tutorial explica como realizar um teste t de duas amostras no Excel.

Como realizar um teste t de duas amostras no Excel

Suponha que os investigadores queiram saber se duas espécies de plantas diferentes num determinado país têm a mesma altura média. Como demoraria muito para medir cada planta, eles decidiram colher uma amostra de 20 plantas de cada espécie.

A imagem a seguir mostra a altura (em polegadas) de cada planta em cada amostra:

Podemos realizar um teste t de duas amostras para determinar se as duas espécies têm a mesma altura média seguindo estas etapas:

Etapa 1: Determine se as variâncias da população são iguais .

Quando realizamos um teste t para duas amostras, devemos primeiro decidir se assumiremos que as duas populações têm variâncias iguais ou desiguais. Geralmente, podemos assumir que as populações têm variâncias iguais se a razão entre a maior variância amostral e a menor variância amostral for inferior a 4:1.

Podemos encontrar a variação de cada amostra usando a função Excel =VAR.S(Cell range) , conforme mostrado na imagem a seguir:

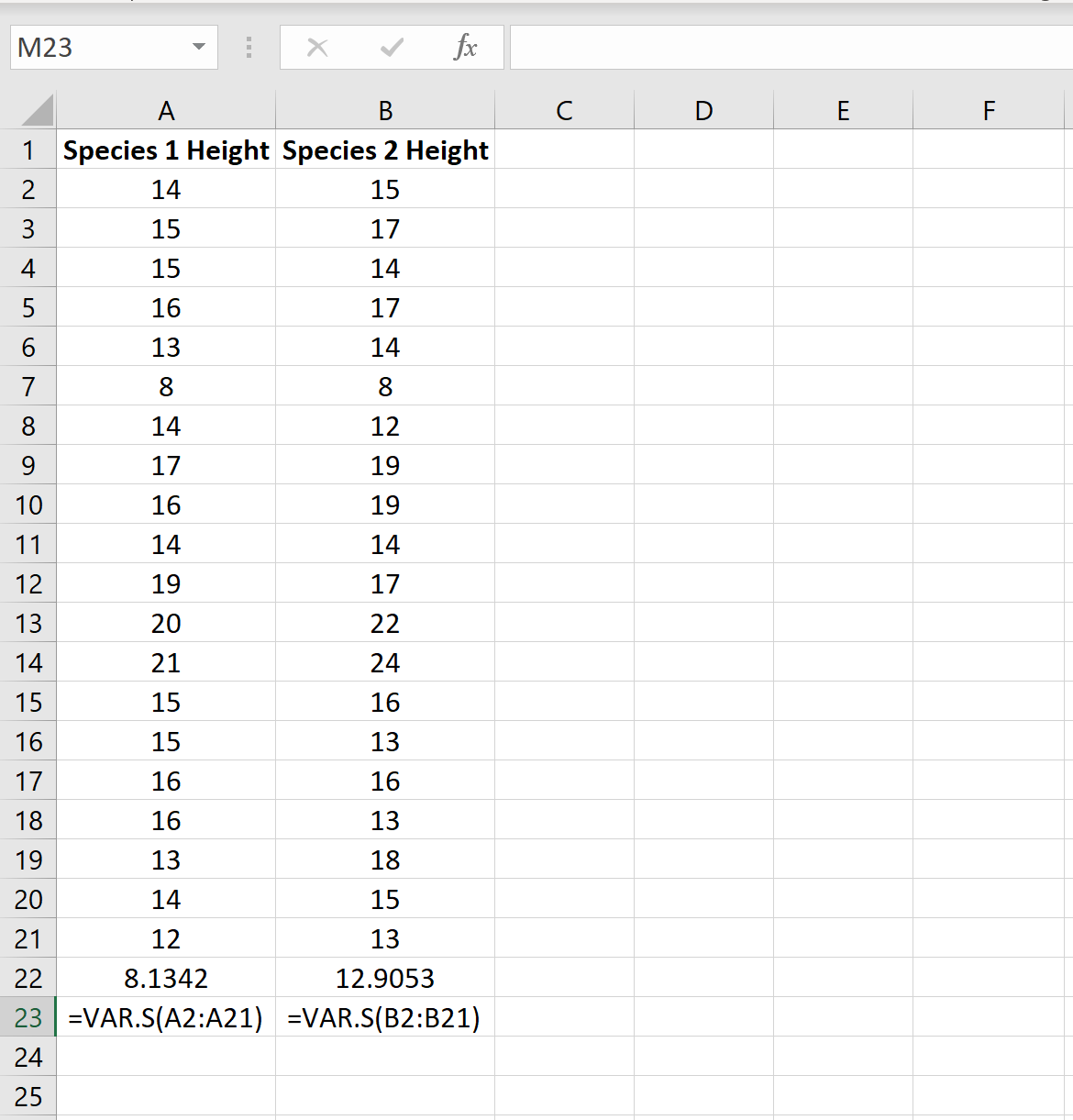
A razão entre a maior variância amostral e a menor variância amostral é 12,9053/8,1342 = 1,586 , que é menor que 4. Isso significa que podemos assumir que as variâncias populacionais são iguais.

Etapa 2: Abra o Analysis ToolPak .

Na guia Dados da faixa superior, clique em “Análise de Dados”.

Se você não vir esta opção para clicar, primeiro você precisa baixar o Analysis ToolPak , que é totalmente gratuito.

Etapa 3: Selecione o teste apropriado a ser usado.

Selecione a opção que diz teste t: duas amostras assumindo variações iguais e clique em OK.

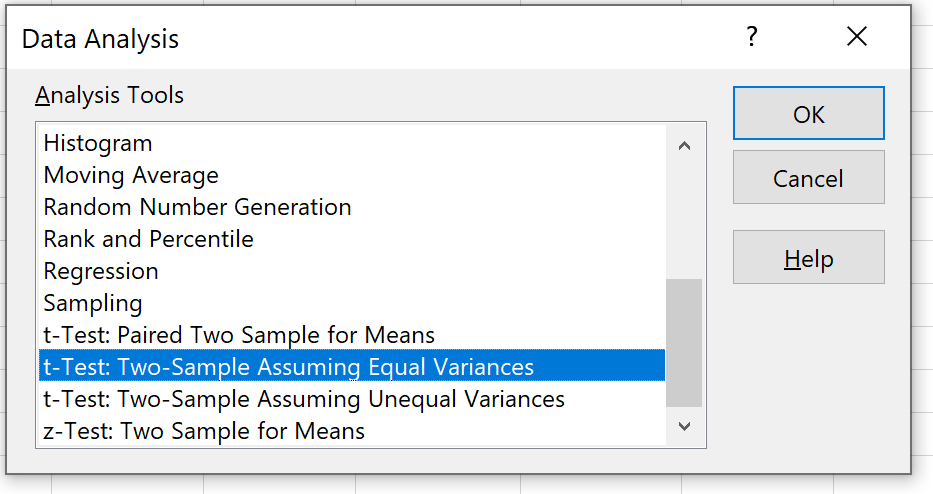
Passo 4: Insira as informações necessárias .

Insira o intervalo de valores para a variável 1 (nossa primeira amostra), variável 2 (nossa segunda amostra), diferença média hipotética (neste caso colocamos “0” porque queremos saber se a verdadeira diferença média da população é 0) e o intervalo de saída no qual gostaríamos de ver os resultados do teste t exibidos. Em seguida, clique em OK.

Etapa 5: Interprete os resultados .

Depois de clicar em OK na etapa anterior, os resultados do teste t serão exibidos.

Veja como interpretar os resultados:

Média: Esta é a média de cada amostra. A amostra 1 tem altura média de 15,15 e a amostra 2 tem altura média de 15,8 .

Variância: Esta é a variação de cada amostra. A amostra 1 tem uma variância de 8,13 e a amostra 2 tem uma variância de 12,90 .

Observações: Este é o número de observações em cada amostra. Ambas as amostras contêm 20 observações (por exemplo, 20 plantas individuais em cada amostra).

Variância agrupada: número calculado “agrupando” as variâncias de cada amostra usando a fórmula s ² _p = [ (n ₁ -1)s ² ₁ + (n ₂ -1)s ² ₂ ] / (n ₁ +n ₂ – 2), que resulta em 10,51974 . Este número é então usado no cálculo da estatística do teste t .

Diferença média hipotética: O número sobre o qual “fazemos uma hipótese” é a diferença entre as médias das duas populações. Neste caso, escolhemos 0 porque queremos testar se a diferença entre as médias das duas populações é ou não igual a 0, por exemplo, se não há diferença.

df: Os graus de liberdade para o teste t, calculados como n ₁ + n ₂ -2 = 20 + 20 – 2 = 38 .

t Stat: A estatística de teste t , calculada como t = [ x ₁ – x ₂ ] / √ [s ² _p (1/n ₁ + 1/n ₂ )]

Neste caso, t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .

P(T<=t) bicaudal: o valor p para um teste t bicaudal. Neste caso, p = 0,530047 . Isso é muito maior que alfa = 0,05, portanto não rejeitamos a hipótese nula. Não temos evidências suficientes para dizer que as médias das duas populações são diferentes.

t Crítico bicaudal: Este é o valor crítico do teste, encontrado identificando o valor na tabela de distribuição t que corresponde a um teste bicaudal com alfa = 0,05 e df = 38. Isso resulta em 2, 024394 . Como nossa estatística de teste t é menor que esse valor, não conseguimos rejeitar a hipótese nula. Não temos evidências suficientes para dizer que as médias das duas populações são diferentes.

Observe que a abordagem do valor p e do valor crítico levará à mesma conclusão.

Recursos adicionais

Os tutoriais a seguir explicam como realizar outros tipos de testes t no Excel:

Como realizar um teste t de uma amostra no Excel
Como realizar um teste t de amostras pareadas no Excel