Como construir um intervalo de previsão no excel
Em estatística, a regressão linear simples é uma técnica que podemos usar para quantificar a relação entre uma variável preditora, x, e uma variável de resposta, y.
Quando realizamos uma regressão linear simples, obtemos uma “linha de melhor ajuste” que descreve a relação entre x e y, que pode ser escrita como:
ŷ=b 0 + b 1 x
Ouro:
- ŷ é o valor previsto da variável de resposta
- b 0 é a interceptação y
- b 1 é o coeficiente de regressão
- x é o valor da variável preditora
Às vezes queremos usar esta linha de melhor ajuste para construir um intervalo de previsão para um determinado valor de x 0 , que é um intervalo em torno do valor previsto ŷ 0 tal que haja uma probabilidade de 95% de que o verdadeiro valor de y na população correspondente a x 0 está incluído neste intervalo.
A fórmula para calcular o intervalo de previsão para um determinado valor x 0 é escrita:
ŷ 0 +/- t α/2,df=n-2 * se
Ouro:
se = S yx √(1 + 1/n + (x 0 – x ) 2 /SS x )
A fórmula pode parecer um pouco intimidante, mas na verdade é simples de calcular no Excel. A seguir veremos um exemplo de uso desta fórmula para calcular um intervalo de previsão para um determinado valor no Excel.
Exemplo: como construir um intervalo de previsão no Excel
O conjunto de dados a seguir mostra o número de horas estudadas, bem como a nota do exame obtida por 15 alunos diferentes:
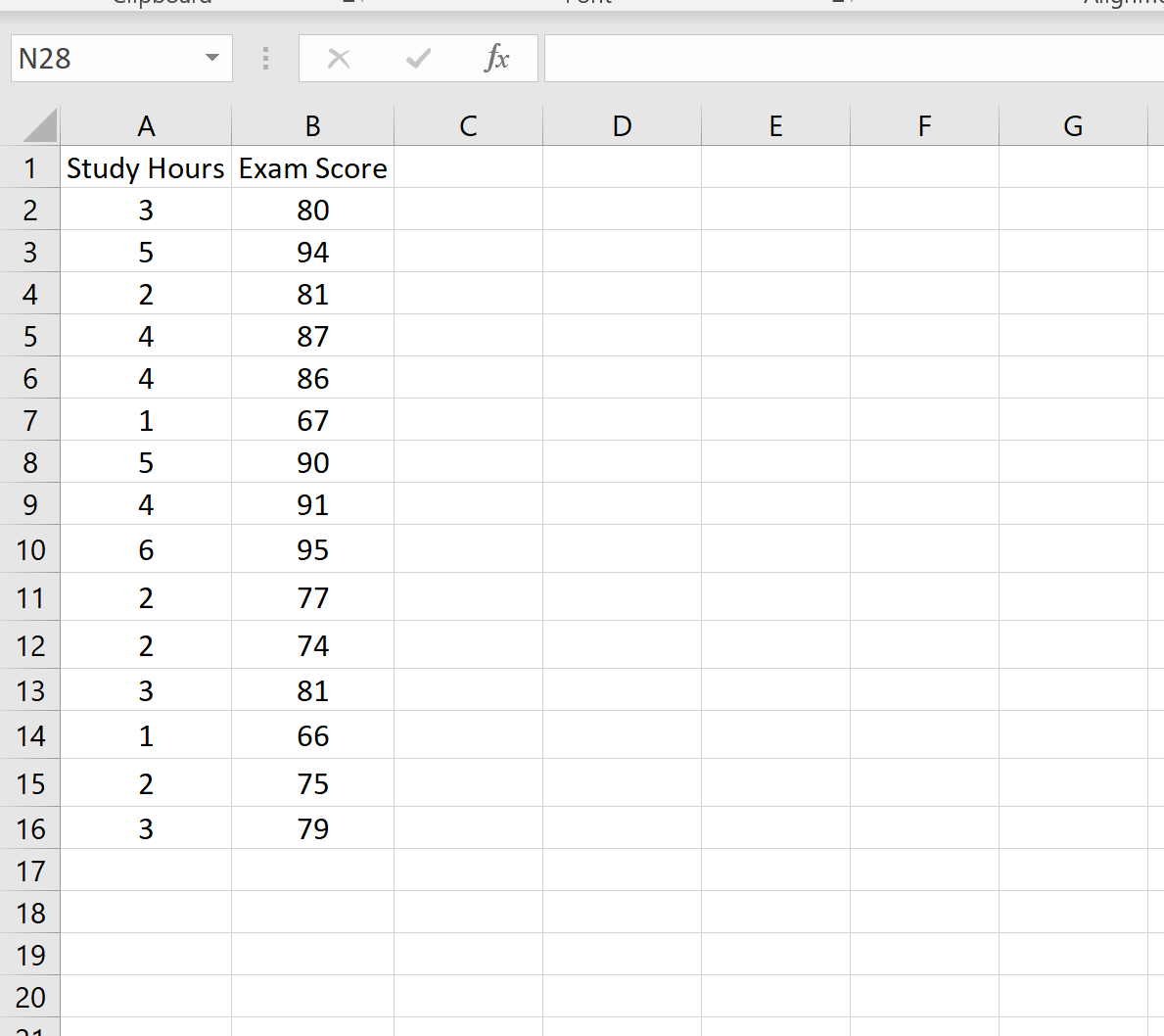
Suponha que queiramos criar um intervalo de previsão de 95% para o valor x 0 = 3. Ou seja, queremos criar um intervalo tal que haja 95% de probabilidade de que a nota do exame fique dentro desse intervalo para um aluno que estuda para 3 horas.
A captura de tela a seguir mostra como calcular todos os valores necessários para obter esse intervalo de previsão.
Nota: As fórmulas da coluna F mostram como foram calculados os valores da coluna E.
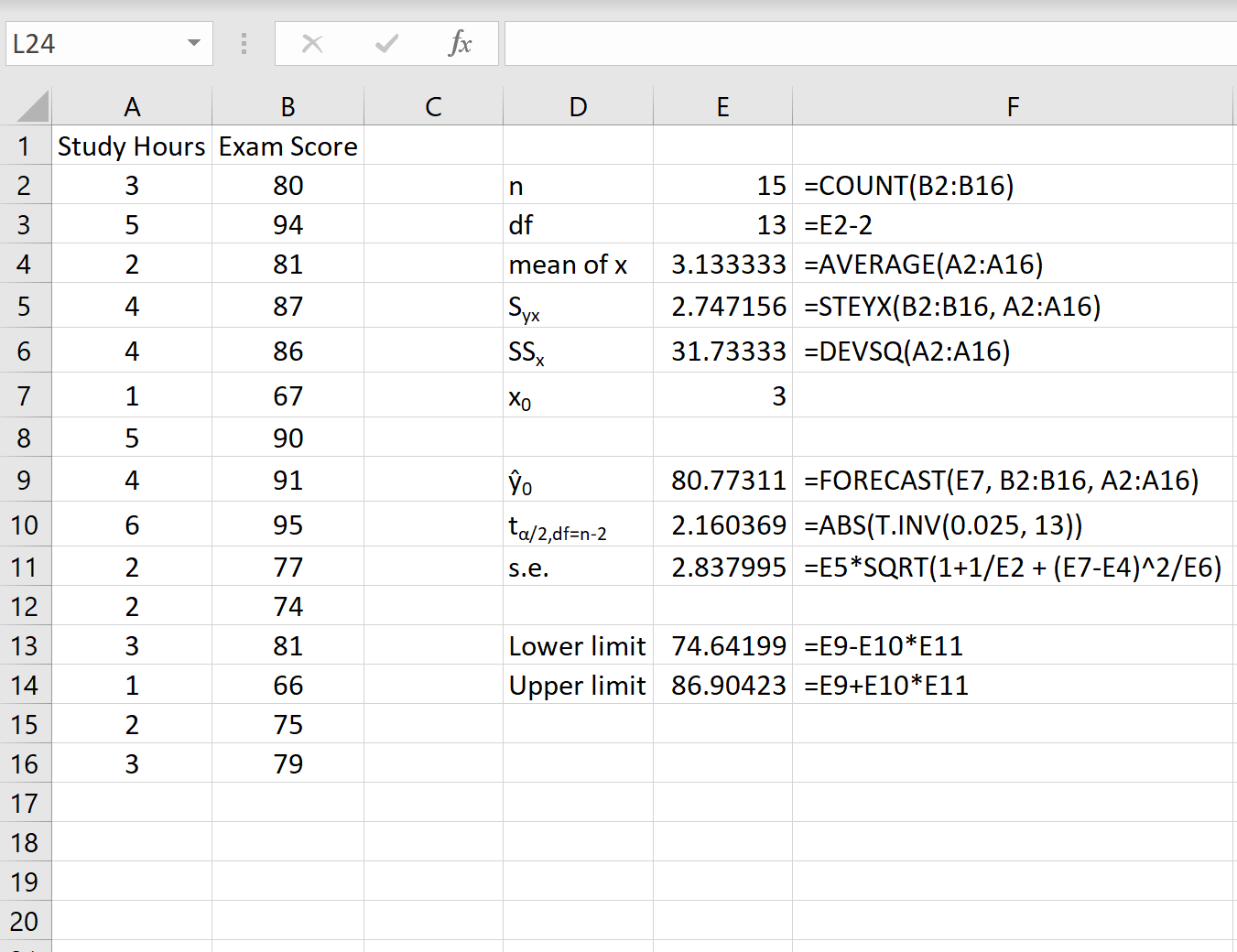
O intervalo de previsão de 95% para um valor de x 0 = 3 é (74,64, 86,90) . Ou seja, prevemos com 95% de probabilidade que um aluno que estude 3 horas obterá uma nota entre 74,64 e 86,90.
Algumas notas sobre os cálculos utilizados:
- Para calcular o valor t-crítico de t α/2,df=n-2, usamos α/2 = 0,05/2 = 0,25, pois queríamos um intervalo de predição de 95%. Observe que intervalos de previsão mais altos (por exemplo, intervalo de previsão de 99%) levarão a intervalos mais amplos. Por outro lado, um intervalo de previsão menor (por exemplo, um intervalo de previsão de 90%) levará a um intervalo mais estreito.
- Usamos a fórmula =FORECAST() para obter o valor previsto para ŷ 0 , mas a fórmula =FORECAST.LINEAR() retornará exatamente o mesmo valor.