Uma explicação simples da correção de continuidade nas estatísticas
A correção de continuidade é aplicada quando você deseja usar uma distribuição contínua para aproximar uma distribuição discreta. Geralmente, é usado quando se deseja usar uma distribuição normal para aproximar uma distribuição binomial .
Lembre-se de que a distribuição binomial nos diz a probabilidade de obter x sucesso em n tentativas, dado que a probabilidade de sucesso em uma única tentativa é p . Para responder perguntas sobre probabilidade com distribuição binomial, poderíamos simplesmente usar uma calculadora de distribuição binomial , mas também poderíamos aproximar a probabilidade usando uma distribuição normal com correção de continuidade.
Uma correção de continuidade é o nome dado à adição ou subtração de 0,5 de um valor discreto de x .
Por exemplo, digamos que queremos determinar a probabilidade de uma moeda cair com cara menor ou igual a 45 vezes ao longo de 100 lançamentos. Ou seja, queremos encontrar P(X ≤ 45). Para usar a distribuição normal para aproximar a distribuição binomial, encontraríamos P(X ≤ 45,5).
A tabela a seguir mostra quando você deve adicionar ou subtrair 0,5, dependendo do tipo de probabilidade que você está tentando encontrar:
| Use a distribuição binomial | Usando a distribuição normal com correção de continuidade |
|---|---|
| X = 45 | 44,5 < X < 45,5 |
| X ≤ 45 | X < 45,5 |
| X < 45 | X < 44,5 |
| X ≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Observação:
Só é apropriado aplicar uma correção de continuidade à distribuição normal para aproximar a distribuição binomial quando n*p e n*(1-p) são ambos pelo menos 5.
Por exemplo, suponha n = 15 e p = 0,6. Nesse caso:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Como ambos os números são maiores ou iguais a 5, seria aceitável aplicar uma correção de continuidade neste cenário.
O exemplo a seguir ilustra como aplicar uma correção de continuidade à distribuição normal para aproximar a distribuição binomial.
Exemplo de aplicação de correção de continuidade
Suponha que queiramos saber a probabilidade de uma moeda cair com cara menor ou igual a 43 vezes em 100 lançamentos. Nesse caso:
n = número de tentativas = 100
X = número de sucessos = 43
p = probabilidade de sucesso em uma determinada tentativa = 0,50
Podemos inserir esses números na calculadora de distribuição binomial para ver que a probabilidade de a moeda cair em cara menor ou igual a 43 vezes é 0,09667 .
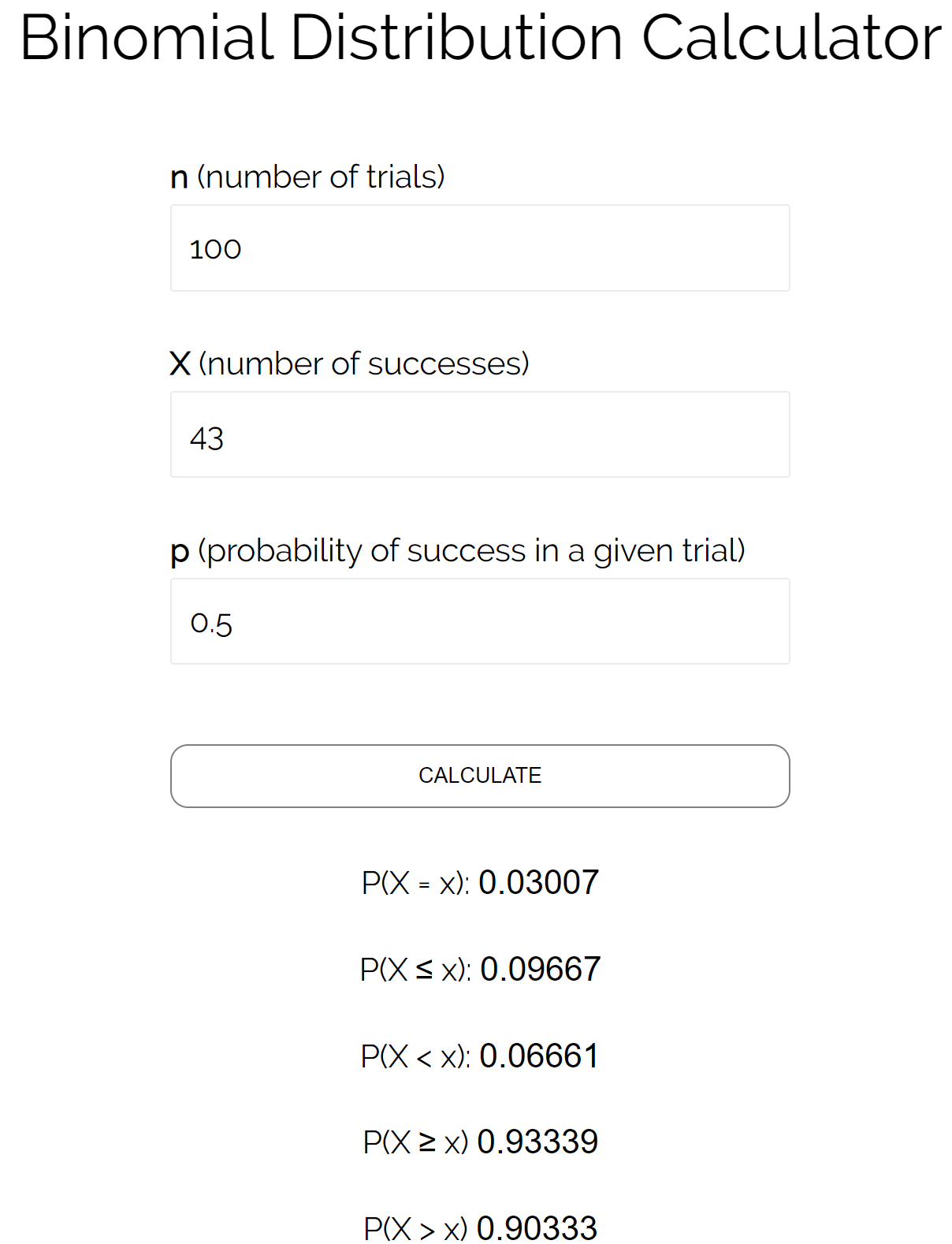
Para aproximar a distribuição binomial aplicando uma correção de continuidade à distribuição normal, podemos usar os seguintes passos:
Etapa 1: verifique se n*p e n*(1-p) são pelo menos 5 .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Ambos os números são maiores ou iguais a 5, então podemos continuar.
Etapa 2: determinar se deseja adicionar ou subtrair 0,5
Referindo-nos à tabela acima, vemos que devemos somar 0,5 quando trabalhamos com probabilidade na forma de X ≤ 43. Assim, encontraremos P(X< 43,5).
Etapa 3: Encontre a média (μ) e o desvio padrão (σ) da distribuição binomial.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*0,5*(1-0,5) = √ 25 = 5
Passo 4: Encontre o escore z usando a média e o desvio padrão encontrados na etapa anterior.
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
Etapa 5: Use a tabela Z para encontrar a probabilidade associada ao escore z.
De acordo com a Tabela Z, a probabilidade associada a z = -1,3 é 0,0968 .
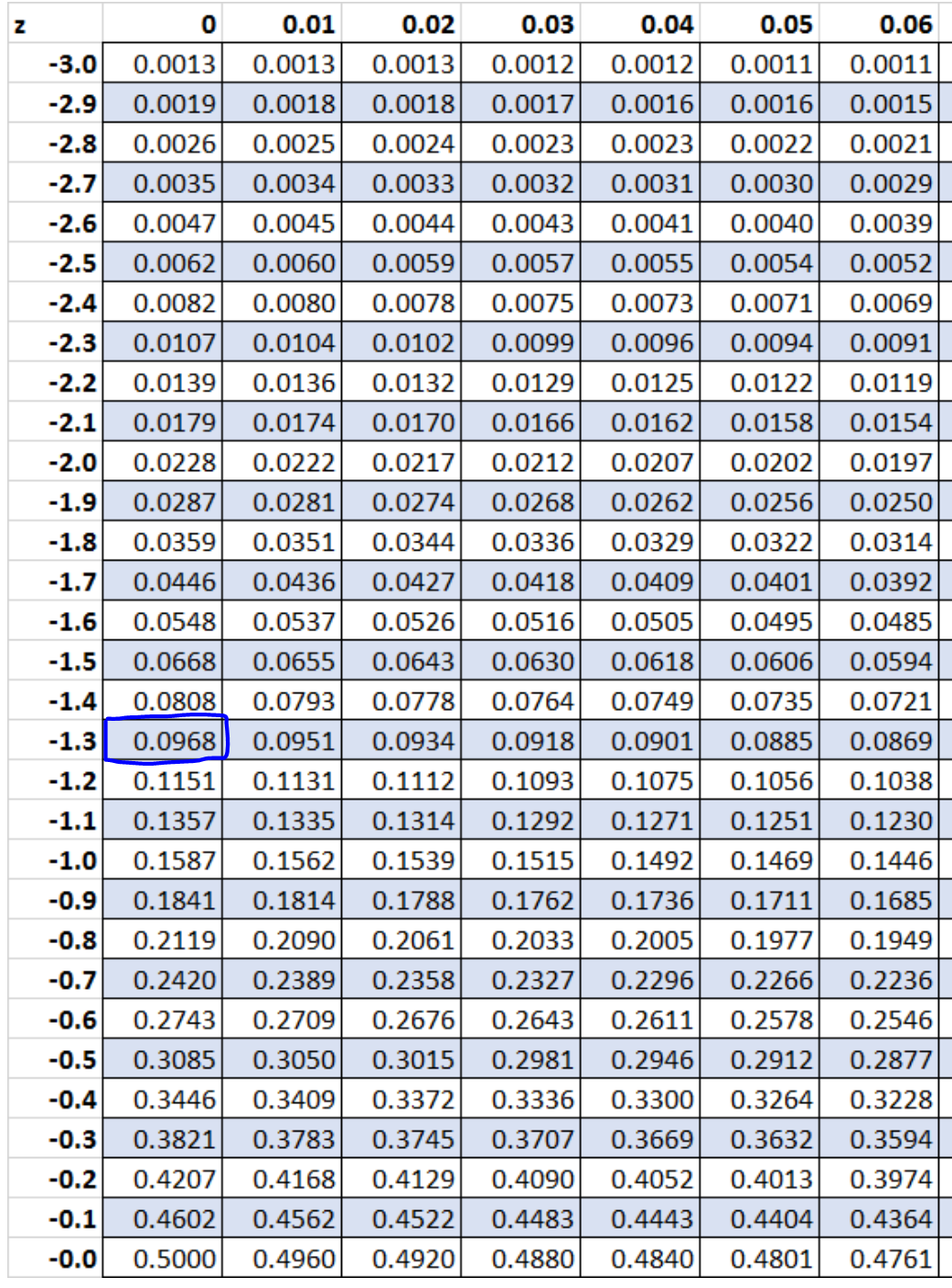
Portanto, a probabilidade exata que encontramos usando a distribuição binomial foi 0,09667 , enquanto a probabilidade aproximada que encontramos usando a correção de continuidade com a distribuição normal foi 0,0968 . Esses dois valores são bastante fechados.
Quando usar a correção de continuidade
Antes de existirem softwares estatísticos modernos e os cálculos terem que ser feitos manualmente, as correções de continuidade eram frequentemente usadas para encontrar probabilidades envolvendo distribuições discretas. Hoje, as correções de continuidade desempenham um papel menor no cálculo de probabilidades, uma vez que geralmente podemos confiar em software ou calculadoras para calcular probabilidades para nós.
Em vez disso, é simplesmente um tópico abordado em cursos de estatística para ilustrar a relação entre uma distribuição binomial e uma distribuição normal e para mostrar que é possível que uma distribuição normal se aproxime de uma distribuição binomial aplicando uma correção de continuidade.
Calculadora de correção de continuidade
Use a calculadora de correção de continuidade para aplicar automaticamente uma correção de continuidade a uma distribuição normal para aproximar probabilidades binomiais.