Como interpretar razões de probabilidade
Nas estatísticas, probabilidade se refere às chances de um evento ocorrer. É calculado da seguinte forma:
PROBABILIDADE:
P (evento) = (# resultados desejáveis) / (# resultados possíveis)
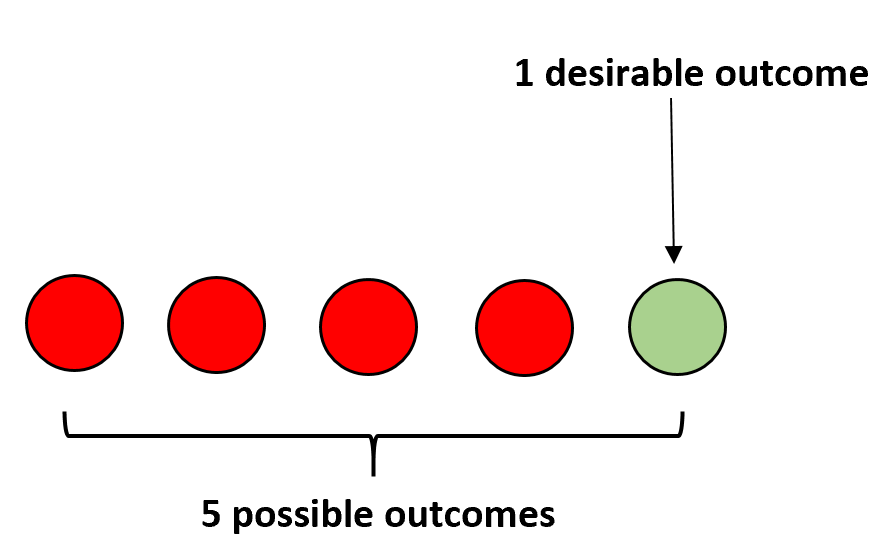
Por exemplo, suponha que temos quatro bolas vermelhas e uma bola verde num saco. Se você fechar os olhos e selecionar uma bola aleatoriamente, a probabilidade de você escolher uma bola verde será calculada da seguinte forma:
P(verde) = 1/5 = 0,2 .
As chances de um evento ocorrer podem ser calculadas da seguinte forma:
CHANCES:
Chances (evento) = P (ocorre o evento) / 1-P (ocorre o evento)
Por exemplo, as chances de arremessar uma bola verde são (0,2)/1-(0,2) = 0,2/0,8 = 0,25 .
A razão de chances é a razão entre duas probabilidades.
RELATÓRIO DE SORTE:
Probabilidades = Probabilidades do Evento A / Probabilidades do Evento B
Por exemplo, poderíamos calcular a razão de probabilidade entre escolher uma bola vermelha e uma bola verde.
A probabilidade de tirar uma bola vermelha é 4/5 = 0,8 .
As chances de tirar uma bola vermelha são (0,8) / 1-(0,8) = 0,8 / 0,2 = 4 .
A razão de chances para escolher uma bola vermelha em vez de uma bola verde é calculada da seguinte forma:
Probabilidades (vermelho) / Probabilidades (verde) = 4 / 0,25 = 16 .
Portanto, as chances de acertar uma bola vermelha são 16 vezes maiores do que as chances de acertar uma bola verde.
Quando as taxas de probabilidade são usadas no mundo real?
No mundo real, os rácios de probabilidades são utilizados numa variedade de contextos em que os investigadores pretendem comparar as probabilidades de ocorrência de dois eventos. Aqui estão alguns exemplos.
Exemplo #1: Interpretando odds ratios
Os pesquisadores querem saber se um novo tratamento aumenta as chances de um paciente ter um resultado positivo de saúde em comparação com um tratamento existente. A tabela a seguir mostra o número de pacientes que tiveram um resultado de saúde positivo ou negativo, dependendo do tratamento.

As chances de um paciente obter um resultado positivo com o novo tratamento podem ser calculadas da seguinte forma:
Chances = P(positivo) / 1 – P(positivo) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25
As chances de um paciente obter um resultado positivo com o tratamento existente podem ser calculadas da seguinte forma:
Chances = P(positiva) / 1 – P(positiva) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875
Assim, a razão de probabilidade de alcançar um resultado positivo com o novo tratamento em comparação com o tratamento existente pode ser calculada da seguinte forma:
Razão de probabilidade = 1,25 / 0,875 = 1,428 .
Interpretamos isso como significando que as chances de um paciente ter um resultado positivo usando o novo tratamento são 1,428 vezes as chances de um paciente ter um resultado positivo usando o tratamento existente.
Ou seja, as chances de obter resultado positivo aumentam em 42,8% com o novo tratamento.
Exemplo #2: Interpretando odds ratios
Os profissionais de marketing querem saber se um anúncio faz com que os clientes comprem um determinado item com mais frequência do que outro anúncio. Então, eles mostram cada anúncio para 100 pessoas. A tabela a seguir mostra o número de pessoas que compraram o item, com base no anúncio que viram:
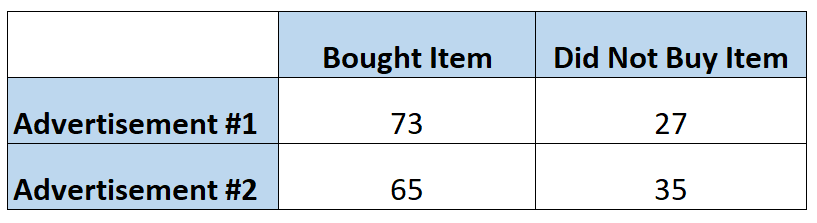
As chances de um indivíduo comprar o item após ver o primeiro anúncio podem ser calculadas da seguinte forma:
Probabilidades = P(comprado) / 1 – P(comprado) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704
As chances de um indivíduo comprar o item após ver o segundo anúncio podem ser calculadas da seguinte forma:
Probabilidades = P(comprado) / 1 – P(comprado) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857
Portanto, a proporção de chances de um cliente comprar o item depois de ver o primeiro anúncio versus comprar depois de ver o segundo anúncio pode ser calculada da seguinte forma:
Razão de probabilidade = 2,704 / 1,857 = 1,456 .
Interpretamos isso como significando que as chances de um indivíduo comprar o item depois de ver o primeiro anúncio são 1,456 vezes as chances de um indivíduo comprar o item depois de ver o segundo anúncio.
Ou seja, as chances de compra do item aumentam em 45,6% graças à primeira listagem.
Recursos adicionais
Como calcular a razão de chances e o risco relativo no Excel
Como interpretar uma razão de chances menor que 1
Como interpretar o risco relativo