Como realizar um teste t de uma amostra no stata

Um teste t de uma amostra é usado para testar se a média de uma população é ou não igual a um determinado valor.

Este tutorial explica como realizar um teste t de uma amostra no Stata.

Exemplo: teste t de uma amostra no Stata

Os pesquisadores querem saber se os automóveis viajam em média 20 milhas por galão. Eles coletam uma amostra de 74 carros e desejam realizar um teste T de amostra para determinar se a verdadeira média de mpg é 20 ou não.

Conclua as etapas a seguir para realizar um teste t de uma amostra.

Etapa 1: carregar dados.

Primeiro, carregue os dados digitando use https://www.stata-press.com/data/r13/auto na caixa de comando e clicando em Enter.

Etapa 2: visualize os dados brutos.

Antes de realizar um teste t de uma amostra, vamos primeiro examinar os dados brutos. Na barra de menu superior, navegue até Dados > Editor de dados > Editor de dados (navegar) . Isso nos mostrará um monte de informações sobre cada um dos 74 carros, mas lembre-se de que estamos interessados apenas em milhas por galão (a coluna mpg ):

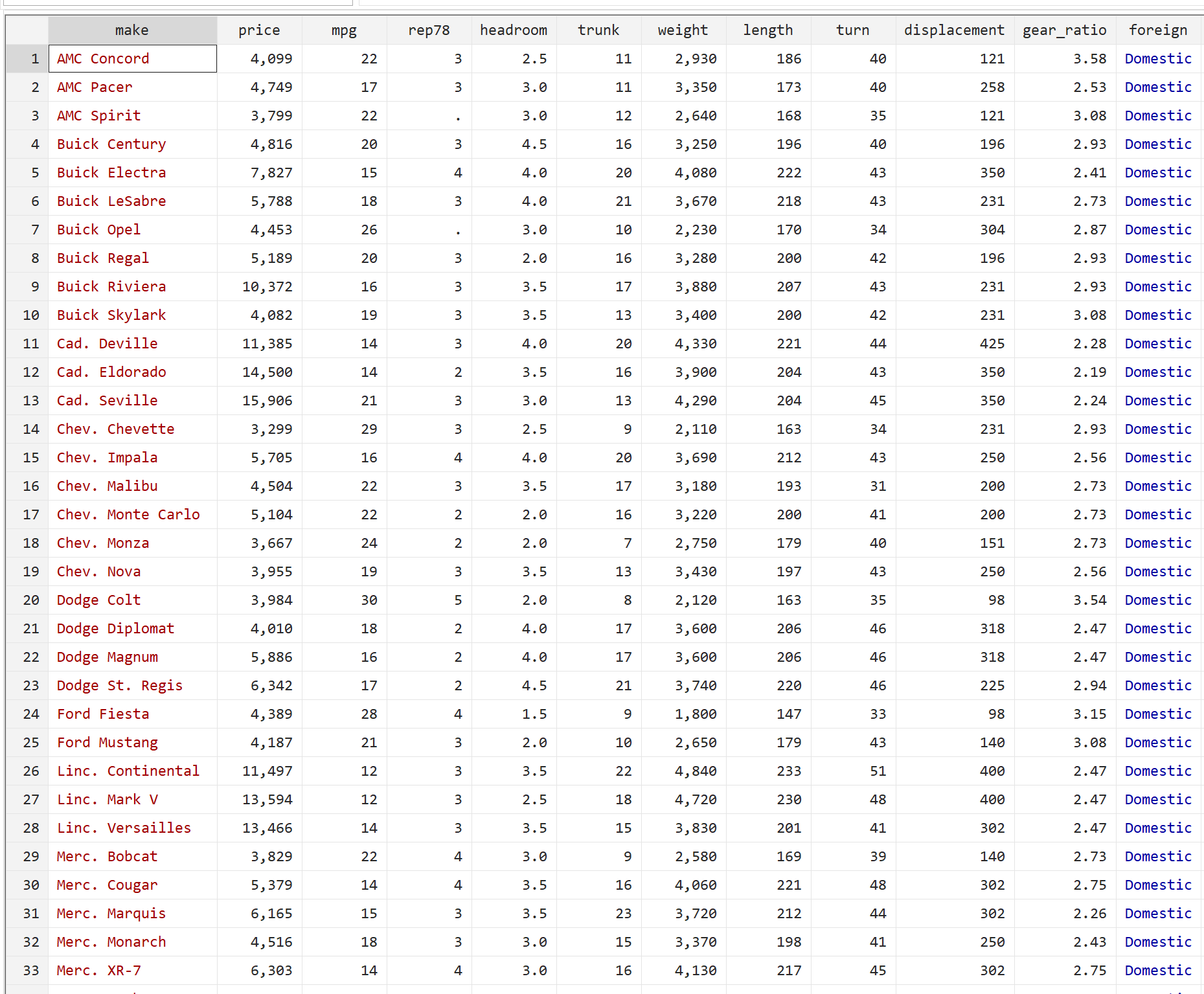
Etapa 3: execute um teste t de uma amostra.

Na barra de menu superior, navegue até Estatísticas > Resumos, Tabelas e Testes > Testes de Hipóteses Clássicos > Teste t (teste de comparação de médias) .

Mantenha uma amostra selecionada . Para Nome da variável, escolha mpg . Para Média Hipotética, insira 20 . Para Nível de confiança, escolha o nível desejado. Um valor de 95 corresponde a um nível de significância de 0,05. Deixaremos isso em 95. Por fim, clique em OK .

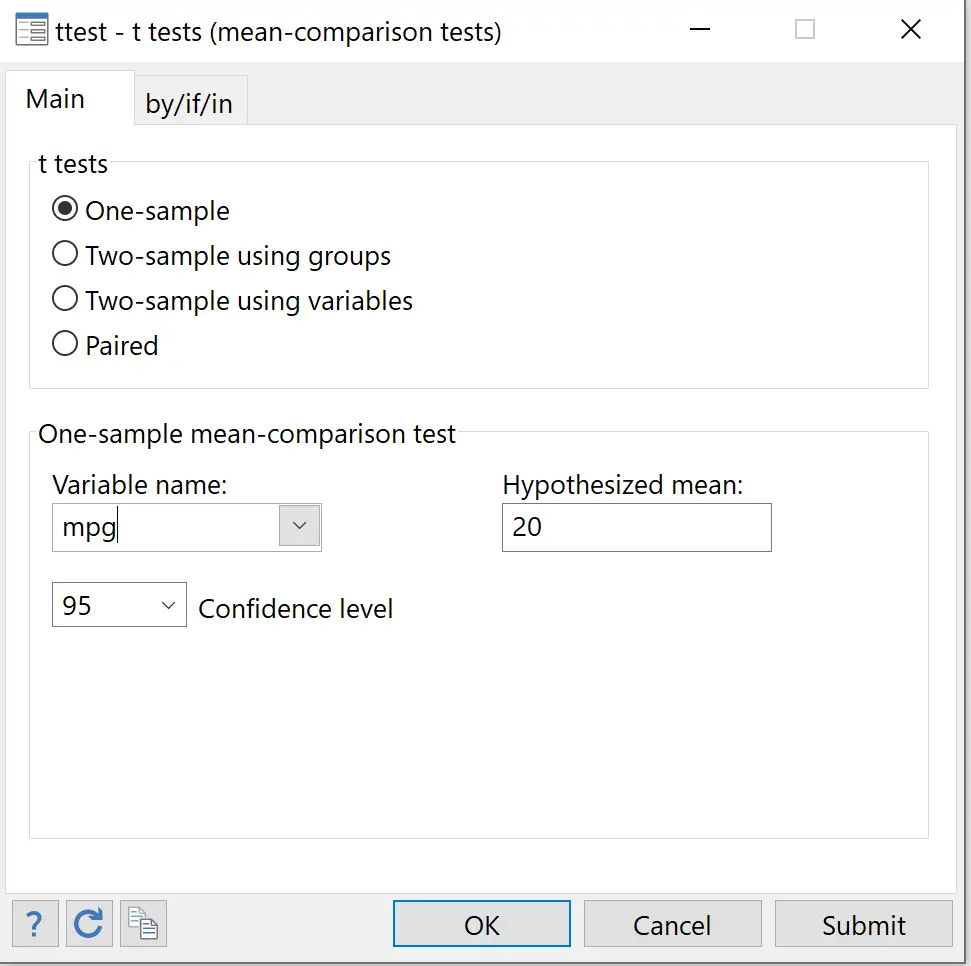
Os resultados do teste t de uma amostra serão exibidos:

Veja como interpretar os resultados:

Obs: O número de observações. Nesse caso, são 74 carros no total.

Média: O mpg médio de todos os carros. Nesse caso, a média é de 21,2973 milhas por galão.

Padrão. Err: calculado como σ / √ n = 5,785503 / √ 74 = 0,6725511.

Padrão. Dev: o desvio padrão de mpg. Neste caso é 5,785503.

95% Conf. Intervalo: intervalo de confiança de 95% para a verdadeira média populacional.

t: A estatística de teste, calculada como (x – u) / (σ / √n ) = (21,2973-20) / 5,785503 / √74 = 1,9289.

graus de liberdade: graus de liberdade a serem usados para o teste t, calculados como n-1 = 74-1 = 73.

Os valores p para três testes t diferentes de uma amostra são mostrados na parte inferior dos resultados. Como queremos entender se a verdadeira média de mpg é 20 ou não, examinaremos os resultados do teste intermediário (no qual a hipótese alternativa é Ha: média! = 20) que tem um valor p de 0,0576 .

Como este valor não está abaixo do nosso nível de significância de 0,05, não rejeitamos a hipótese nula. Não temos evidências suficientes para dizer que o verdadeiro mpg médio para esta população de carros seja algo diferente de 20 mpg.

Etapa 4: relatar os resultados.

Finalmente, relataremos os resultados do nosso teste t de uma amostra. Aqui está um exemplo de como fazer isso:

Um teste t de uma amostra foi realizado em 74 carros para determinar se a média real de mpg da população era diferente de 20 mpg.

Os resultados mostraram que a média real da população não foi diferente de 20 mpg (t = 1,9289 com df = 73, p = 0,0576) a um nível de significância de 0,05.

Um intervalo de confiança de 95% para a verdadeira média populacional deu o intervalo de (19,9569, 22,63769).