Correlações no stata: pearson, spearman e kendall

Nas estatísticas, a correlação refere-se à força e à direção de uma relação entre duas variáveis. O valor de um coeficiente de correlação pode variar de -1 a 1, com -1 indicando um relacionamento negativo perfeito, 0 indicando nenhum relacionamento e 1 indicando um relacionamento positivo perfeito.

Existem três maneiras comuns de medir a correlação:

Correlação de Pearson: Usada para medir a correlação entre duas variáveis contínuas. (por exemplo, altura e peso)

Correlação de Spearman: Utilizada para medir a correlação entre duas variáveis classificadas. (por exemplo, classificação da pontuação no exame de matemática de um aluno versus a classificação da pontuação no exame de ciências em uma turma)

Correlação de Kendall: Usada quando você deseja usar a correlação de Spearman, mas o tamanho da amostra é pequeno e há muitas classificações relacionadas.

Este tutorial explica como encontrar os três tipos de correlações no Stata.

Carregando dados

Para cada um dos exemplos a seguir, usaremos um conjunto de dados chamado auto . Você pode carregar este conjunto de dados digitando o seguinte na caixa Comando:

use https://www.stata-press.com/data/r13/auto

Podemos ter uma visão geral rápida do conjunto de dados digitando o seguinte na caixa de comando:

resumir

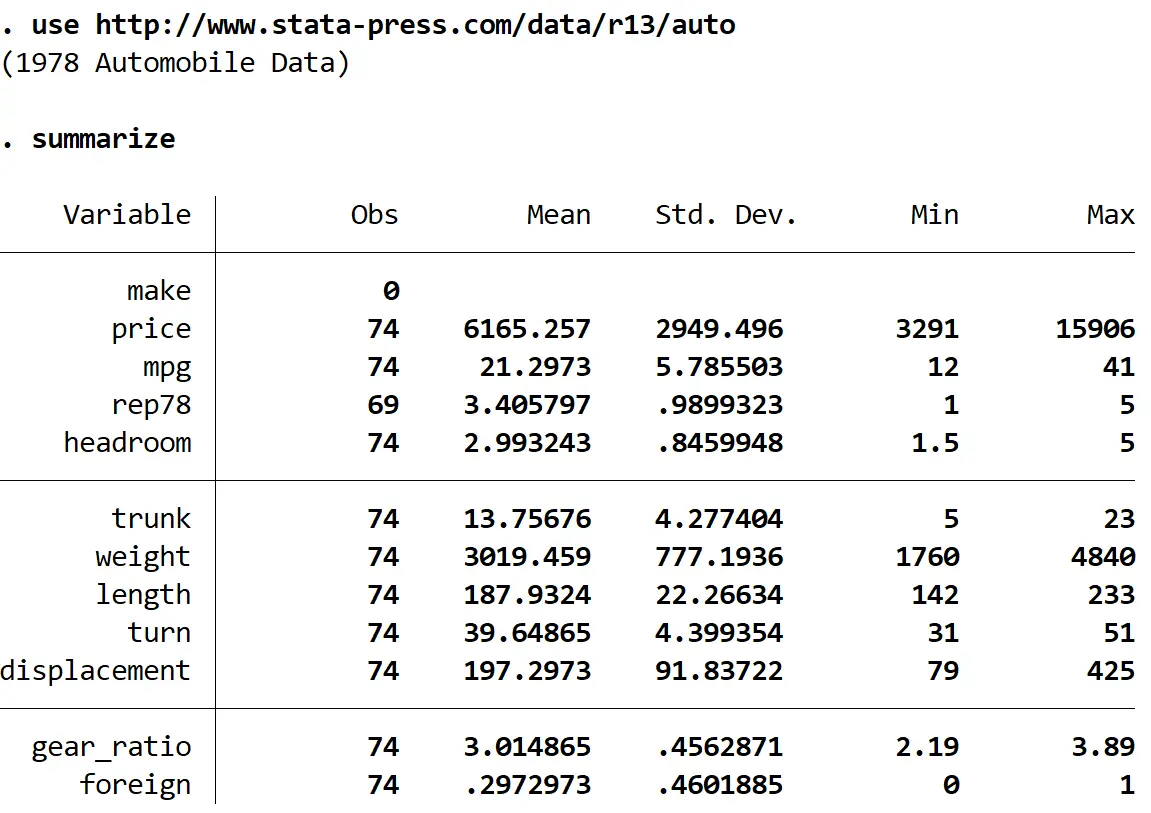
Podemos ver que existem 12 variáveis no total no conjunto de dados.

Como encontrar a correlação de Pearson no Stata

Podemos encontrar o coeficiente de correlação de Pearson entre as variáveis de peso e comprimento usando o comando pwcorr :

comprimento do peso pwcorr

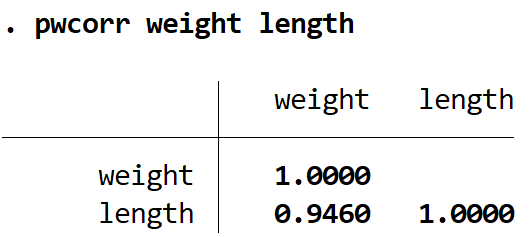
O coeficiente de correlação de Pearson entre estas duas variáveis é de 0,9460 . Para determinar se este coeficiente de correlação é significativo, podemos encontrar o valor de p usando o comando sig :

comprimento do peso pwcorr, sig

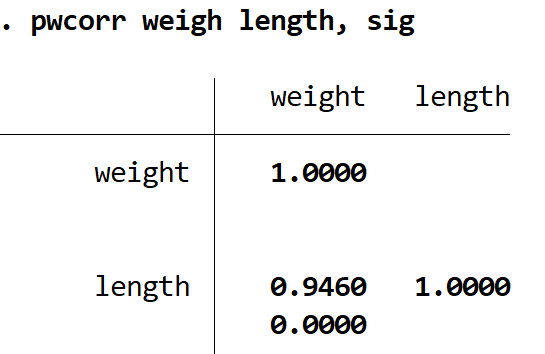
O valor p é 0,000 . Como é inferior a 0,05, a correlação entre estas duas variáveis é estatisticamente significativa.

Para encontrar o coeficiente de correlação de Pearson para múltiplas variáveis, basta digitar uma lista de variáveis após o comando pwcorr :

deslocamento do comprimento do peso pwcorr, sig

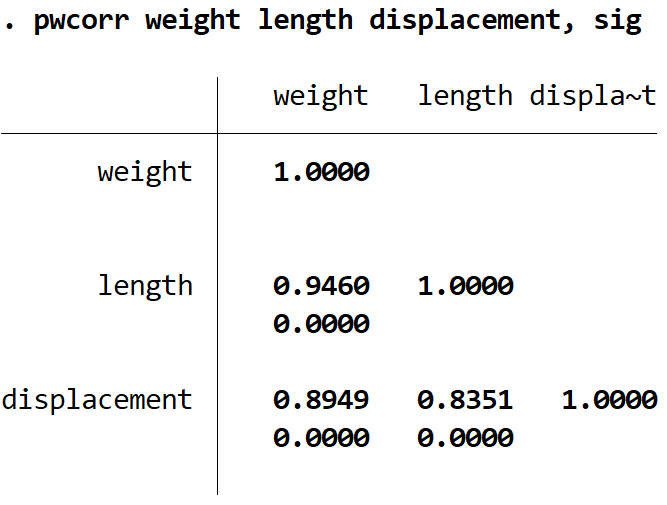
Veja como interpretar o resultado:

• Correlação de Pearson entre peso e comprimento = 0,9460 | valor p = 0,000
• Correlação de Pearson entre peso e deslocamento = 0,8949 | valor p = 0,000
• Correlação de Pearson entre deslocamento e comprimento = 0,8351 | valor p = 0,000

Como encontrar a correlação de Spearman no Stata

Podemos encontrar o coeficiente de correlação de Spearman entre as variáveis trunk e rep78 utilizando o comando spearman :

tronco de lança rep78

Veja como interpretar o resultado:

• Número de obs: Este é o número de observações pareadas usadas para calcular o coeficiente de correlação de Spearman. Como faltavam alguns valores para a variável rep78 , o Stata usou apenas 69 observações por par (em vez das 74 completas).
• Rho de Spearman: Este é o coeficiente de correlação de Spearman. Neste caso é -0,2235, o que indica que existe uma correlação negativa entre as duas variáveis. À medida que um aumenta, o outro tende a diminuir.
• Problema > |t| : Este é o valor p associado ao teste de hipótese. Neste caso, o valor p é 0,0649, o que indica que não há correlação estatisticamente significativa entre as duas variáveis em α = 0,05.

Podemos encontrar o coeficiente de correlação de Spearman para múltiplas variáveis simplesmente digitando mais variáveis após o comando spearman . Podemos encontrar o coeficiente de correlação e o valor p correspondente para cada correlação pareada usando o comando stats(rho p) :

tronco do lanceiro rep78 gear_ratio, estatísticas (rho p)

Veja como interpretar o resultado:

• Correlação de Spearman entre tronco e rep78 = -0,2235 | valor p = 0,0649
• Correlação de Spearman entre tronco e gear_ratio = -0,5187 | valor p = 0,0000
• Correlação de Spearman entre gear_ratio e rep78 = 0,4275 | valor p = 0,0002

Como encontrar a correlação de Kendall no Stata

Podemos encontrar o coeficiente de correlação de Kendall entre as variáveis trunk e rep78 usando o comando ktau :

tronco ktau rep78

Veja como interpretar o resultado:

• Número de obs: Este é o número de observações pareadas usadas para calcular o coeficiente de correlação de Kendall. Como faltavam alguns valores para a variável rep78 , o Stata usou apenas 69 observações por par (em vez das 74 completas).
• Tau-b de Kendall: Este é o coeficiente de correlação de Kendall entre as duas variáveis. Geralmente usamos esse valor em vez de tau-a porque tau-b faz ajustes em caso de empate. Neste caso, tau-b = -0,1752, indicando correlação negativa entre as duas variáveis.
• Problema > |z| : Este é o valor p associado ao teste de hipótese. Neste caso, o valor p é 0,0662, o que indica que não há correlação estatisticamente significativa entre as duas variáveis em α = 0,05.

Podemos encontrar o coeficiente de correlação de Kendall para múltiplas variáveis simplesmente digitando mais variáveis após o comando ktau . Podemos encontrar o coeficiente de correlação e o valor p correspondente para cada correlação pareada usando o comando stats(taub p) :

ktau tronco rep78 gear_ratio, estatísticas (taub p)

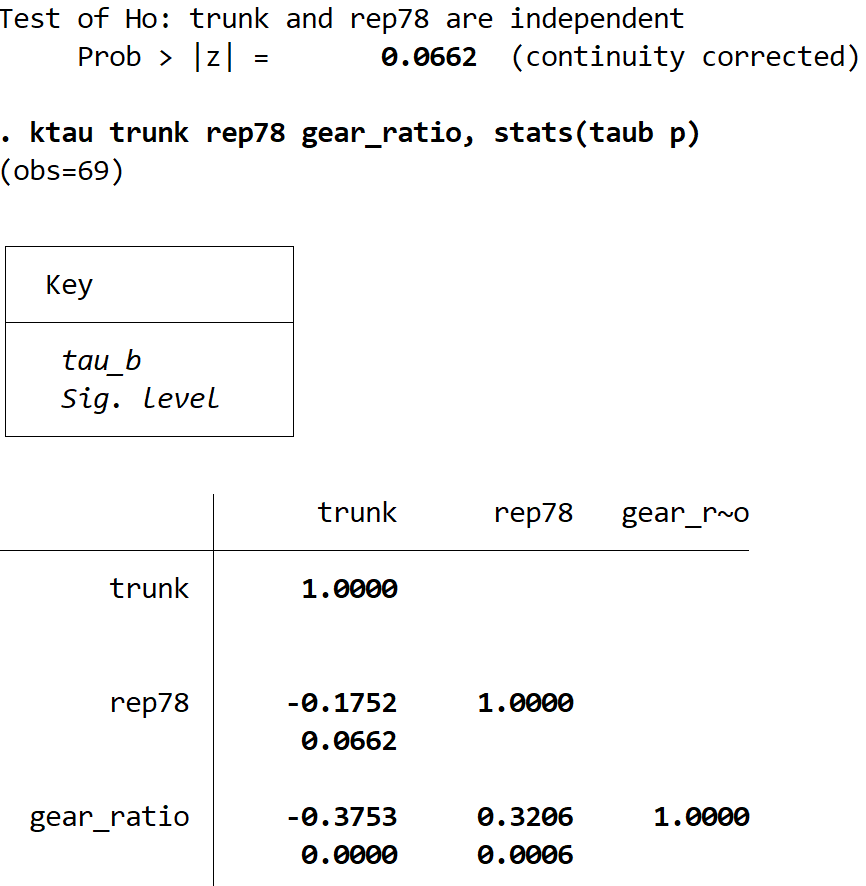
• Correlação de Kendall entre tronco e rep78 = -0,1752 | valor p = 0,0662
• Correlação de Kendall entre tronco e gear_ratio = -0,3753 | valor p = 0,0000
• Correlação de Kendall entre gear_ratio e rep78 = 0,3206 | valor p = 0,0006