Como realizar um teste de kruskal-wallis no stata
Um teste de Kruskal-Wallis é usado para determinar se existe ou não uma diferença estatisticamente significativa entre as medianas de três ou mais grupos independentes. É considerado o equivalente não paramétrico da ANOVA unidirecional .
Este tutorial explica como realizar um teste de Kruskal-Wallis no Stata.
Como realizar um teste de Kruskal-Wallis no Stata
Para este exemplo, usaremos o conjunto de dados do Censo , que contém dados do censo de 1980 para todos os cinquenta estados dos Estados Unidos. No conjunto de dados, os estados são categorizados em quatro regiões diferentes:
- Norte do Leste
- Central norte
- Sul
- Oeste
Realizaremos um teste de Kruskal-Wallis para determinar se a idade mediana é igual nessas quatro regiões.
Etapa 1: Carregar e exibir dados.
Primeiro, carregue o conjunto de dados digitando o seguinte comando na caixa Comando:
use https://www.stata-press.com/data/r13/census
Obtenha um resumo rápido do conjunto de dados usando o seguinte comando:
resumir
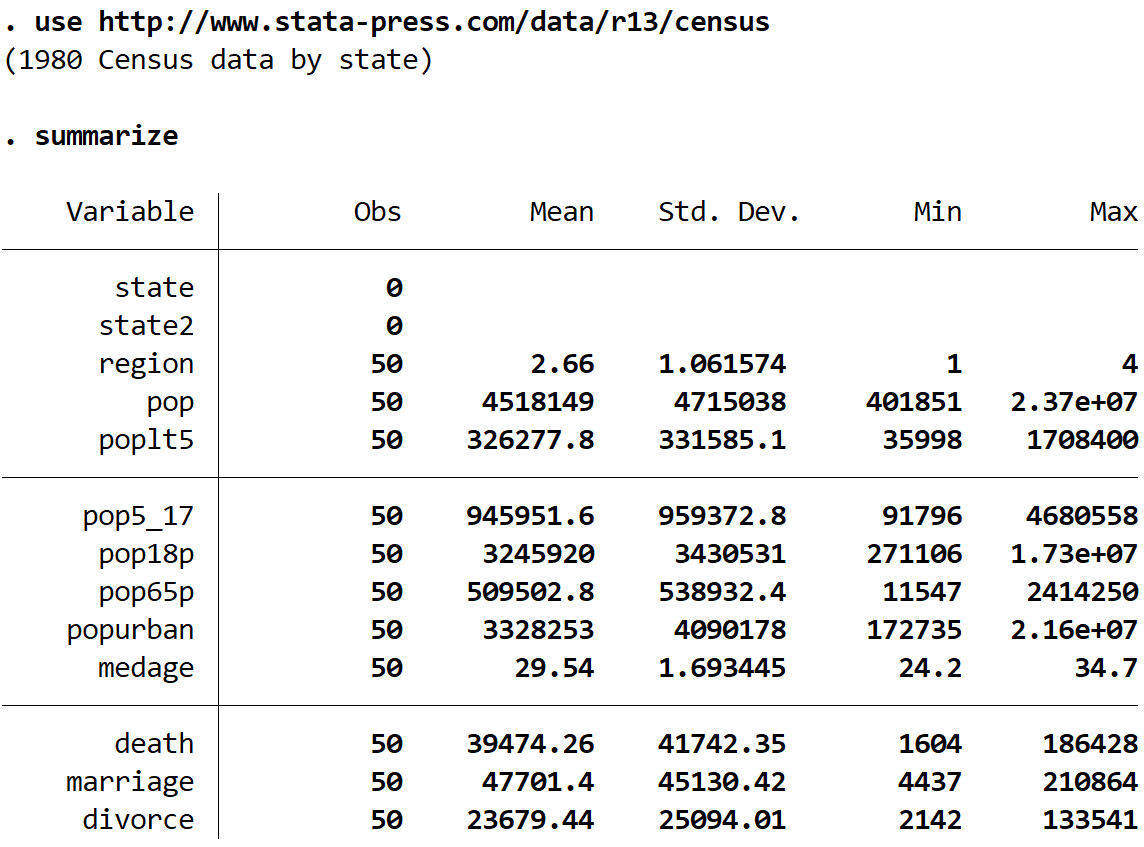
Podemos ver que existem 13 variáveis diferentes neste conjunto de dados, mas as únicas duas com as quais trabalharemos são mediana (idade mediana) e região .
Etapa 2: visualize os dados.
Antes de realizar o teste de Kruskal-Wallis, vamos primeiro criar alguns box plots para visualizar a distribuição mediana da idade para cada uma das quatro regiões:
caixa gráfica Medage, em (região)
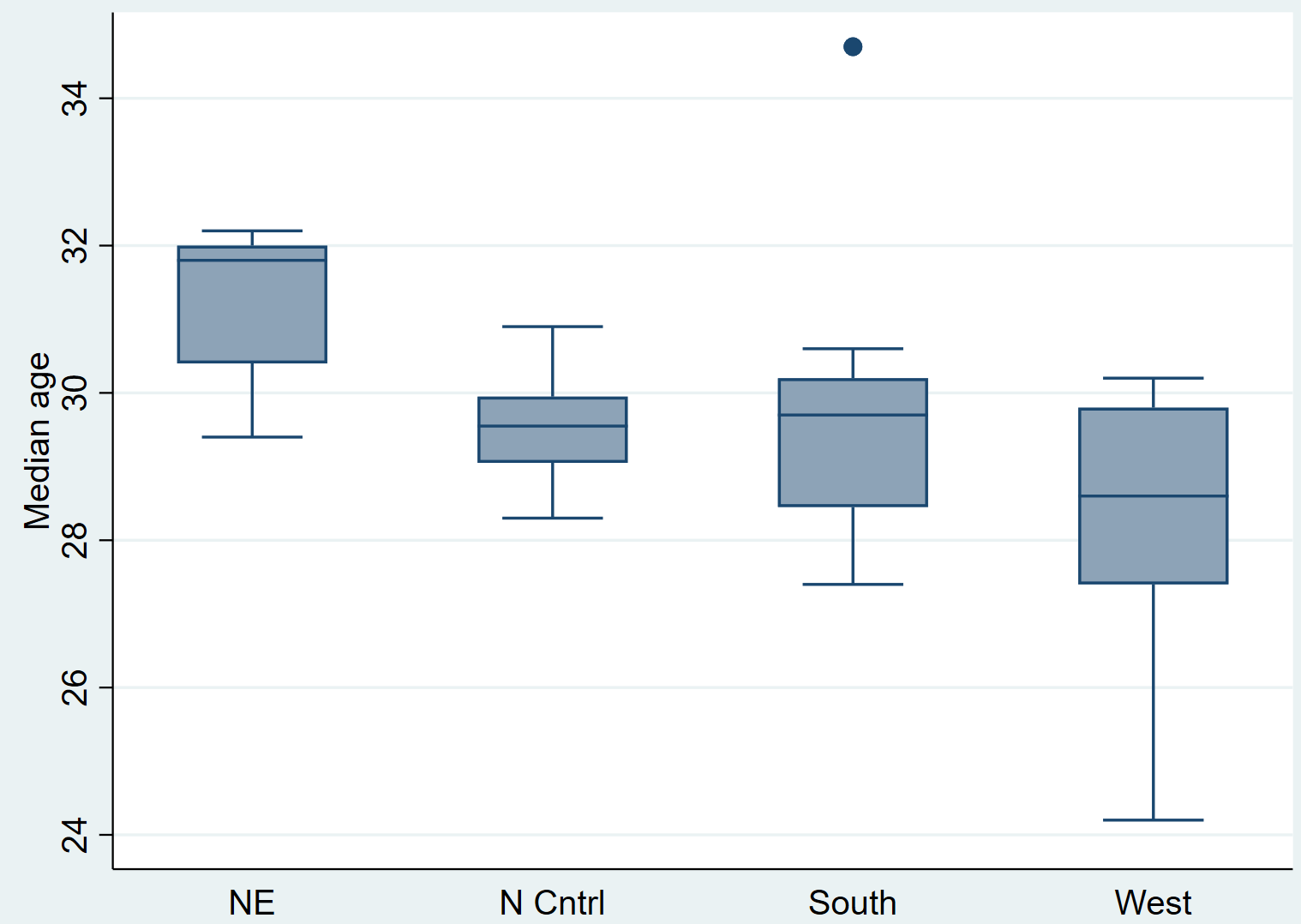
Apenas olhando para os box plots, você pode ver que as distribuições parecem variar de região para região. Em seguida, realizaremos um teste de Kruskal-Wallis para verificar se essas diferenças são estatisticamente significativas.
Etapa 3: execute um teste de Kruskal-Wallis.
Use a seguinte sintaxe para realizar um teste de Kruskal-Wallis:
kwallis medida_variável, por (agrupamento_variável)
No nosso caso, usaremos a seguinte sintaxe:
Medagem kwallis, por (região)
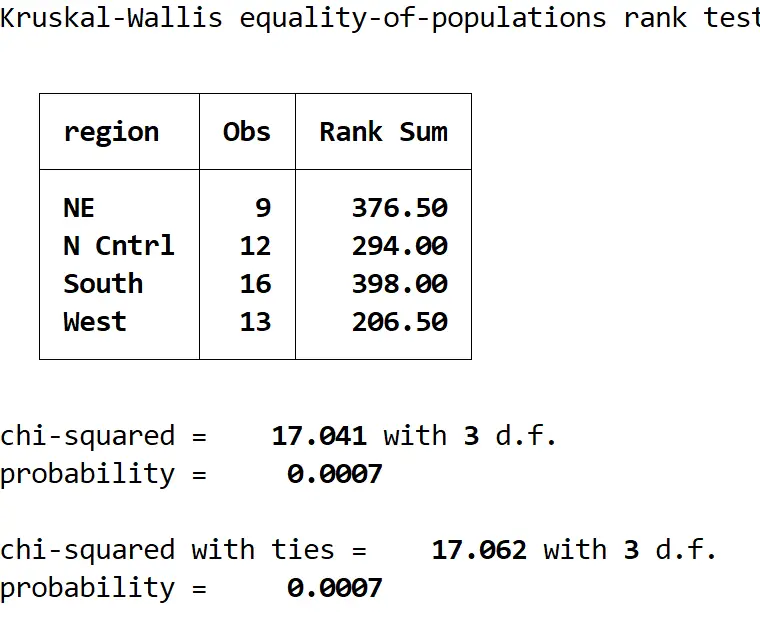
Veja como interpretar o resultado:
Tabela resumo: Esta tabela mostra o número de observações por região e as somas de classificação para cada região.
Qui-quadrado com empates: Este é o valor da estatística de teste, que resulta em 17,062.
probabilidade: este é o valor p que corresponde à estatística de teste, que é 0,0007. Dado que este valor é inferior a 0,05, podemos rejeitar a hipótese nula e concluir que a idade mediana não é igual nas quatro regiões.
Etapa 4: relatar os resultados.
Por fim, gostaríamos de reportar os resultados do teste Kruskal-Wallis. Aqui está um exemplo de como fazer isso:
Um teste de Kruskal-Wallist foi realizado para determinar se a idade mediana dos indivíduos era a mesma nas seguintes quatro regiões dos Estados Unidos:
- Nordeste (n=9)
- Centro-Norte (n=12)
- Sul (n=16)
- Oeste (n=13)
O teste revelou que a mediana de idade dos indivíduos não era a mesma (X 2 = 17,062, p = 0,0007) nas quatro regiões. Ou seja, houve diferença estatisticamente significativa na mediana de idade entre duas ou mais regiões.