Como usar erros padrão robustos em regressão no stata
A regressão linear múltipla é um método que podemos usar para compreender a relação entre múltiplas variáveis explicativas e uma variável de resposta.
Infelizmente, um problema que ocorre frequentemente na regressão é conhecido como heterocedasticidade , no qual há uma mudança sistemática na variância dos resíduos ao longo de um intervalo de valores medidos.
Isto leva a um aumento na variância das estimativas dos coeficientes de regressão, mas o modelo de regressão não leva isso em consideração. Isto torna muito mais provável que um modelo de regressão afirme que um termo do modelo é estatisticamente significativo, quando na realidade não o é.
Uma forma de explicar este problema é usar erros padrão robustos , que são mais “robustos” para o problema da heterocedasticidade e tendem a fornecer uma medida mais precisa do verdadeiro erro padrão de um coeficiente de regressão.
Este tutorial explica como usar erros padrão robustos na análise de regressão no Stata.
Exemplo: erros padrão robustos no Stata
Usaremos o conjunto de dados Stata integrado automaticamente para ilustrar como usar erros padrão robustos na regressão.
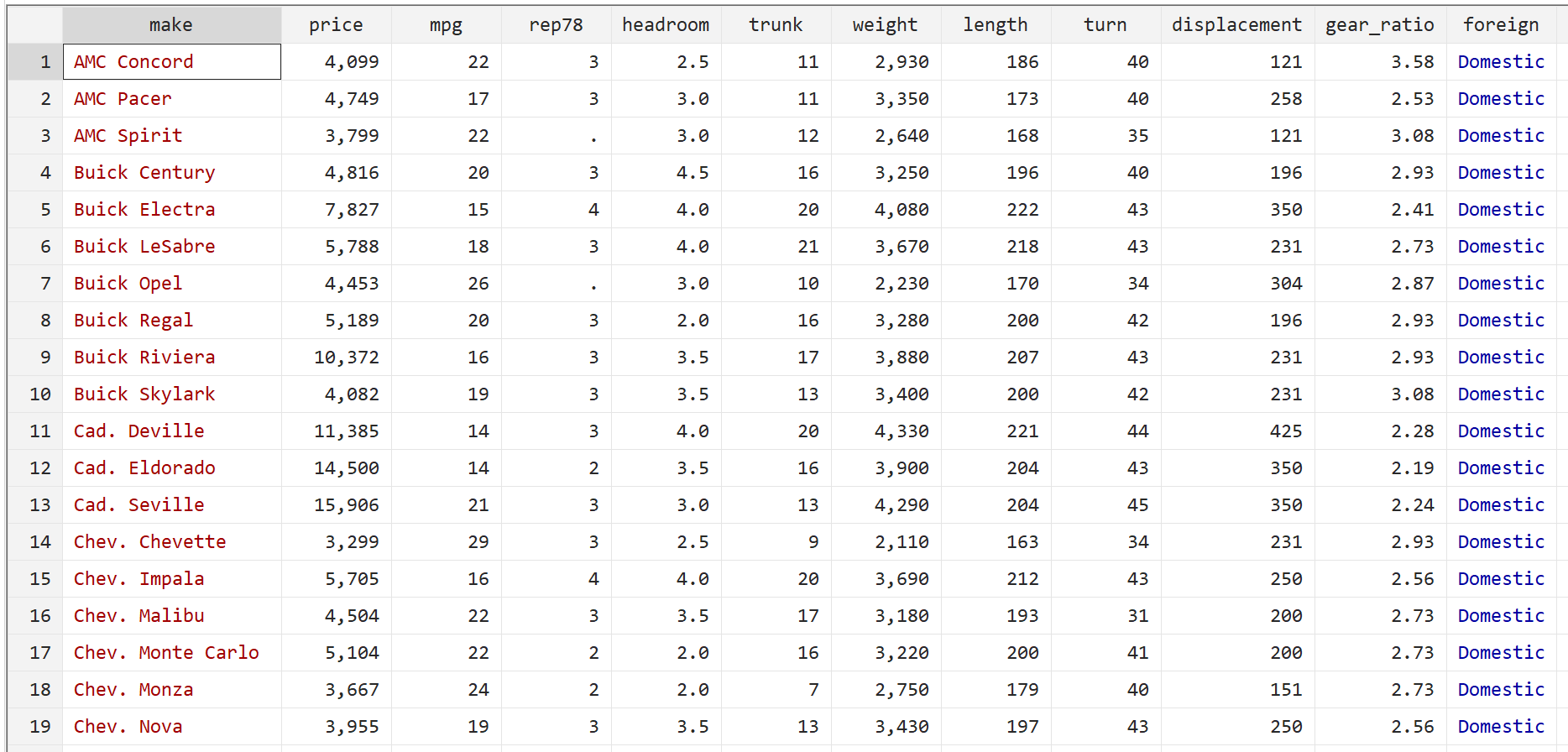
Etapa 1: Carregar e exibir dados.
Primeiro, use o seguinte comando para carregar os dados:
uso automático do sistema
Em seguida, exiba os dados brutos usando o seguinte comando:
br
Etapa 2: Execute a regressão linear múltipla sem erros padrão robustos.
A seguir, inseriremos o seguinte comando para realizar uma regressão linear múltipla usando preço como variável de resposta e mpg e peso como variáveis explicativas:
preço de regressão peso mpg

Etapa 3: Execute a regressão linear múltipla usando erros padrão robustos.
Agora realizaremos exatamente a mesma regressão linear múltipla, mas desta vez usaremos o comando vce(robust) para que o Stata saiba como usar erros padrão robustos:
preço de regressão peso mpg, vce (robusto)
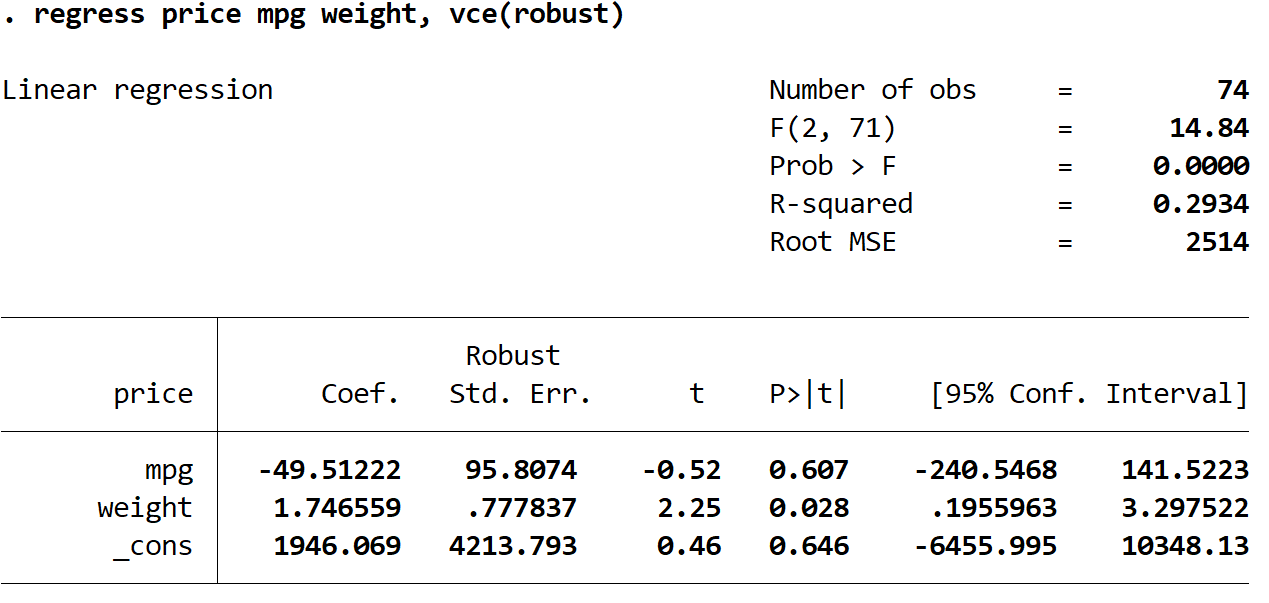
Existem algumas coisas interessantes a serem observadas aqui:
1. As estimativas dos coeficientes permaneceram as mesmas . Quando usamos erros padrão robustos, as estimativas dos coeficientes não mudam em nada. Observe que as estimativas dos coeficientes para mpg, peso e constante são as seguintes para ambas as regressões:
- mpg: -49,51222
- peso: 1,746559
- _contra: 1946.069
2. Os erros padrão mudaram . Observe que quando usamos erros padrão robustos, os erros padrão para cada uma das estimativas dos coeficientes aumentaram.
Nota: Na maioria dos casos, os erros padrão robustos serão maiores do que os erros padrão normais, mas em casos raros é possível que os erros padrão robustos sejam realmente menores.
3. A estatística de teste de cada coeficiente mudou. Observe que o valor absoluto de cada estatística de teste , t , diminuiu. Com efeito, a estatística de teste é calculada como o coeficiente estimado dividido pelo erro padrão. Assim, quanto maior o erro padrão, menor será o valor absoluto da estatística de teste.
4. Os valores p mudaram . Observe que os valores p de cada variável também aumentaram. Isso ocorre porque estatísticas de teste menores estão associadas a valores p maiores.
Embora os valores de p tenham mudado para nossos coeficientes, a variável mpg ainda não é estatisticamente significativa em α = 0,05 e o peso da variável ainda é estatisticamente significativo em α = 0,05.