Como testar a normalidade no stata

Muitos testes estatísticos exigem que uma ou mais variáveis sejam normalmente distribuídas para que os resultados do teste sejam confiáveis.

Este tutorial explica vários métodos que você pode usar para testar a normalidade entre variáveis no Stata.

Para cada um desses métodos, usaremos o conjunto de dados integrado do Stata chamado auto . Você pode carregar este conjunto de dados usando o seguinte comando:

uso automático do sistema

Método 1: histogramas

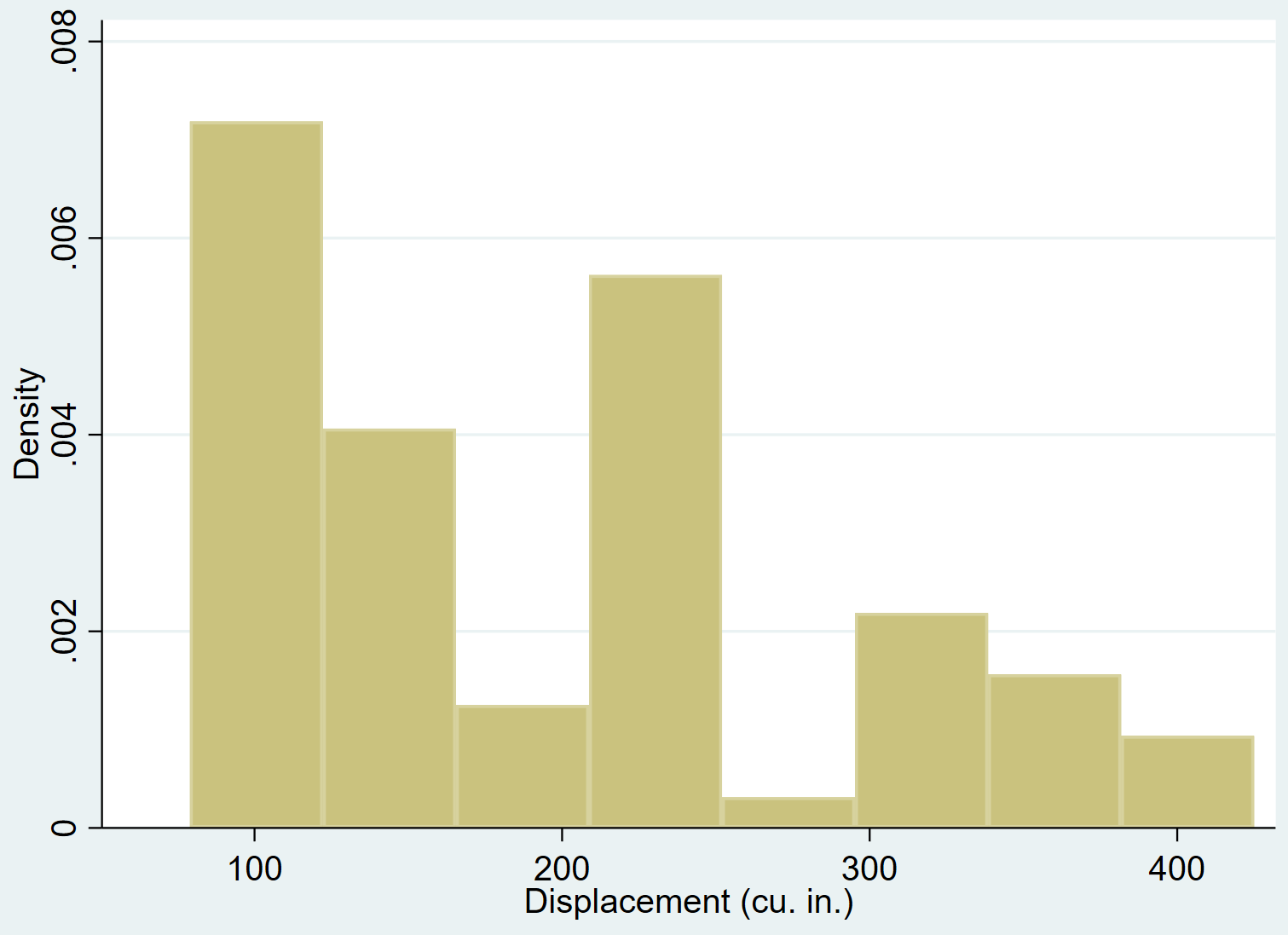
Uma maneira informal de ver se uma variável tem distribuição normal é criar um histograma para exibir a distribuição da variável.

Se a variável tiver distribuição normal, o histograma deve assumir a forma de um “sino” com mais valores localizados próximos ao centro e menos valores localizados nas caudas.

Podemos usar o comando hist para criar um histograma para a variável deslocamento :

história em movimento

Podemos adicionar uma curva de densidade normal a um histograma usando o comando normal :

história em movimento, normal

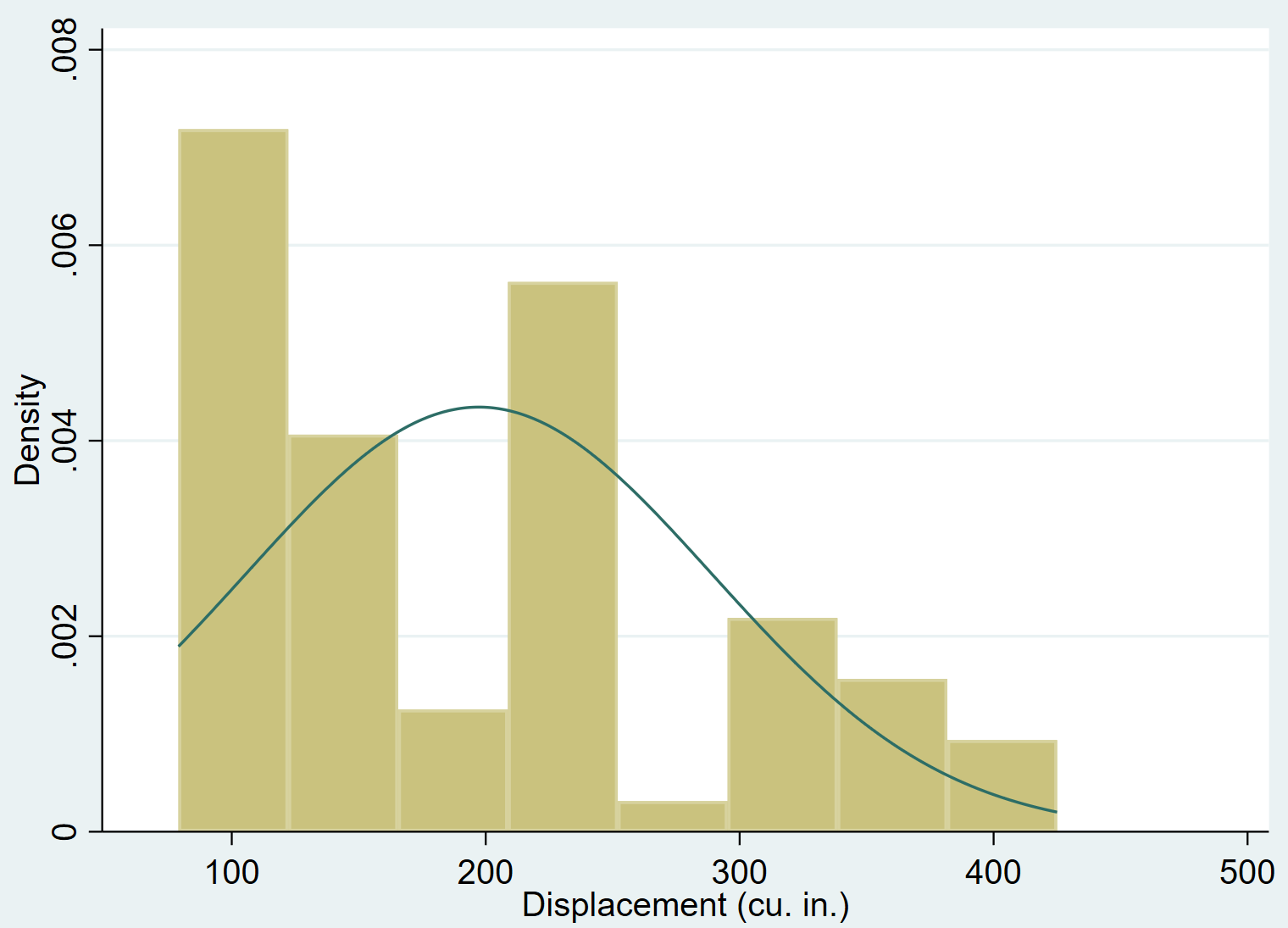
É bastante óbvio que o deslocamento da variável é distorcido para a direita (por exemplo, a maioria dos valores está concentrada à esquerda e uma longa “cauda” de valores se estende para a direita) e não segue uma distribuição normal.

Relacionado: Distribuições distorcidas à esquerda e à direita

Método 2: teste de Shapiro-Wilk

Uma forma formal de testar a normalidade é usar o teste de Shapiro-Wilk .

A hipótese nula para este teste é que a variável tem distribuição normal. Se o valor p do teste estiver abaixo de um certo nível de significância (as escolhas comuns incluem 0,01, 0,05 e 0,10), então podemos rejeitar a hipótese nula e concluir que há evidências suficientes para afirmar que a variável não é normalmente distribuída .

*Este teste pode ser utilizado quando o número total de observações estiver entre 4 e 2.000.

Podemos usar o comando swilk para realizar um teste de Shapiro-Wilk em deslocamento variável:

movimento suave

Veja como interpretar o resultado do teste:

Obs: 74. Este é o número de observações utilizadas no teste.

W: 0,92542. Esta é a estatística de teste do teste.

Prob>z: 0,00031. Este é o valor p associado à estatística de teste.

Como o valor p é inferior a 0,05, podemos rejeitar a hipótese nula do teste. Temos evidências suficientes para dizer que o deslocamento variável não tem distribuição normal.

Também podemos realizar o teste Shapiro-Wilk em múltiplas variáveis ao mesmo tempo, listando múltiplas variáveis após o comando swilk :

comprimento mpg de deslocamento swilk

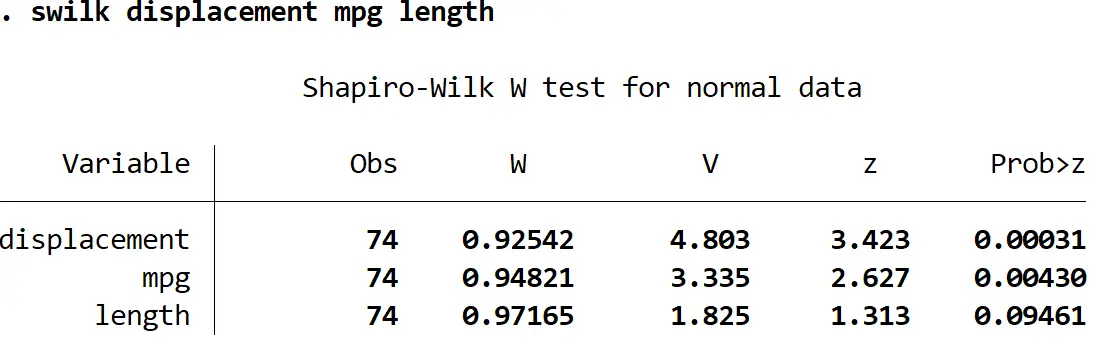
Utilizando um nível de significância de 0,05, concluiríamos que o deslocamento e o mpg não são normalmente distribuídos, mas não temos evidências suficientes para dizer que o comprimento não é normalmente distribuído.

Método 3: teste de Shapiro-Francia

Outra forma formal de testar a normalidade é usar o teste de Shapiro-Francia .

A hipótese nula para este teste é que a variável tem distribuição normal. Se o valor p do teste estiver abaixo de um certo nível de significância, então podemos rejeitar a hipótese nula e concluir que há evidências suficientes para dizer que a variável não tem distribuição normal.

*Este teste pode ser utilizado quando o número total de observações estiver entre 10 e 5.000.

Podemos usar o comando sfrancia para realizar um teste de Shapiro-Wilk em deslocamento variável:

mudança de Sfrancia

Veja como interpretar o resultado do teste:

Obs: 74. Este é o número de observações utilizadas no teste.

W’: 0,93011. Esta é a estatística de teste do teste.

Prob>z: 0,00094. Este é o valor p associado à estatística de teste.

Como o valor p é inferior a 0,05, podemos rejeitar a hipótese nula do teste. Temos evidências suficientes para dizer que o deslocamento variável não tem distribuição normal.

Semelhante ao teste de Shapiro-Wilk, você pode realizar o teste de Shapiro-Francia em diversas variáveis ao mesmo tempo, listando diversas variáveis após o comando sfrancia .

Método 4: teste de assimetria e curtose

Outra forma de testar a normalidade é usar o teste de assimetria e curtose , que determina se a assimetria e a curtose de uma variável são consistentes ou não com a distribuição normal.

A hipótese nula para este teste é que a variável tem distribuição normal. Se o valor p do teste estiver abaixo de um certo nível de significância, então podemos rejeitar a hipótese nula e concluir que há evidências suficientes para dizer que a variável não tem distribuição normal.

*Este teste requer um mínimo de 8 observações para ser usado.

Podemos usar o comando sktest para realizar um teste de assimetria e curtose na variável deslocamento :

movendo o teste

Veja como interpretar o resultado do teste:

Obs: 74. Este é o número de observações utilizadas no teste.

adj chi (2): 5,81. Esta é a estatística do teste qui-quadrado para o teste.

Prob>chi2: 0,0547. Este é o valor p associado à estatística de teste.

Como o valor p não é inferior a 0,05, não rejeitamos a hipótese nula do teste. Não temos provas suficientes para afirmar que os movimentos não são normalmente distribuídos.

Semelhante a outros testes de normalidade, você pode realizar o teste de assimetria e curtose em diversas variáveis ao mesmo tempo, listando diversas variáveis após o comando sktest .