Como testar a multicolinearidade no stata
A multicolinearidade na análise de regressão ocorre quando duas ou mais variáveis explicativas são altamente correlacionadas entre si, de modo que não fornecem informações únicas ou independentes no modelo de regressão. Se o grau de correlação entre as variáveis for alto o suficiente, isso pode causar problemas no ajuste e na interpretação do modelo de regressão.
Por exemplo, suponha que você execute uma regressão linear múltipla com as seguintes variáveis:
Resposta variável: salto vertical máximo
Variáveis explicativas: tamanho do calçado, altura, tempo de prática
Neste caso, as variáveis explicativas tamanho e altura do calçado provavelmente estão fortemente correlacionadas, uma vez que pessoas altas tendem a ter tamanhos de calçado maiores. Isto significa que a multicolinearidade provavelmente será um problema nesta regressão.
Felizmente, é possível detectar multicolinearidade usando uma métrica chamada fator de inflação de variância (VIF) , que mede a correlação e a força da correlação entre variáveis explicativas em um modelo de regressão.
Este tutorial explica como usar VIF para detectar multicolinearidade em uma análise de regressão no Stata.
Exemplo: multicolinearidade no Stata
Para este exemplo, usaremos o conjunto de dados integrado do Stata chamado auto . Use o seguinte comando para carregar o conjunto de dados:
usar automaticamente
Usaremos o comando regress para ajustar um modelo de regressão linear múltipla usando preço como variável de resposta e peso, comprimento e mpg como variáveis explicativas:
preço de regressão peso comprimento mpg
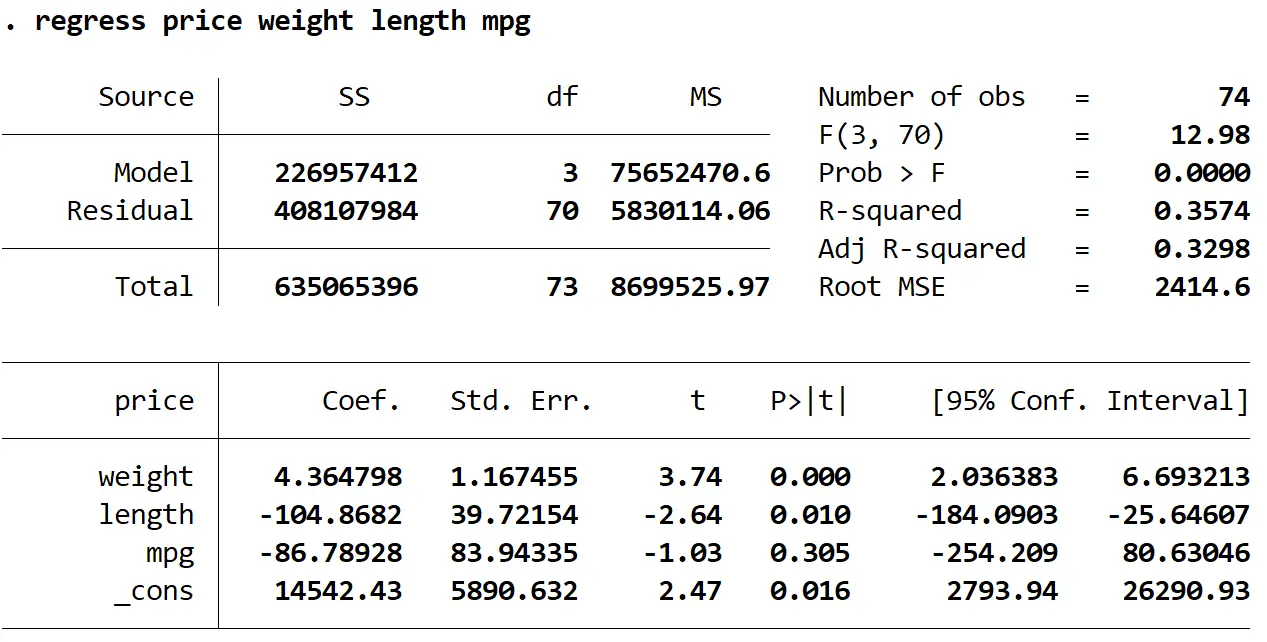
A seguir, usaremos o comando vive para testar a multicolinearidade:
vivaz
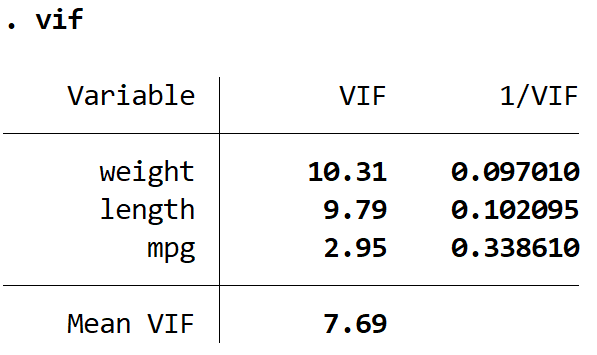
Isso produz um valor VIF para cada uma das variáveis explicativas do modelo. O valor VIF começa em 1 e não tem limite superior. Uma regra geral para interpretar VIFs é:
- Um valor 1 indica que não há correlação entre uma determinada variável explicativa e qualquer outra variável explicativa no modelo.
- Um valor entre 1 e 5 indica uma correlação moderada entre uma determinada variável explicativa e outras variáveis explicativas no modelo, mas muitas vezes não é suficientemente grave para exigir atenção especial.
- Um valor superior a 5 indica uma correlação potencialmente grave entre uma determinada variável explicativa e outras variáveis explicativas do modelo. Nesse caso, as estimativas dos coeficientes e os valores p nos resultados da regressão provavelmente não são confiáveis.
Podemos ver que os valores VIF para peso e comprimento são maiores que 5, indicando que a multicolinearidade é provavelmente um problema no modelo de regressão.
Como lidar com a multicolinearidade
Freqüentemente, a maneira mais fácil de lidar com a multicolinearidade é simplesmente remover uma das variáveis do problema, porque a variável que você está removendo provavelmente é redundante de qualquer maneira e adiciona poucas informações exclusivas ou independentes ao modelo.
Para determinar qual variável remover, podemos usar o comando corr para criar uma matriz de correlação para exibir os coeficientes de correlação entre cada uma das variáveis no modelo, o que pode nos ajudar a identificar quais variáveis podem estar altamente correlacionadas entre si e podem causar o problema de multicolinearidade:
corr preço peso comprimento mpg
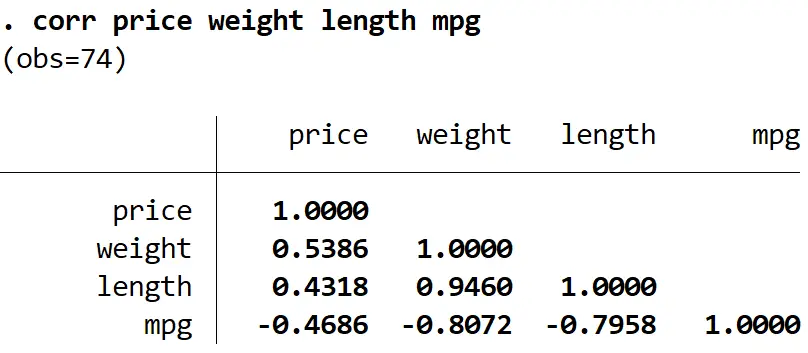
Podemos ver que o comprimento está altamente correlacionado tanto com o peso quanto com o mpg, e tem a menor correlação com o preço da variável de resposta. Assim, a remoção do comprimento do modelo poderia resolver o problema da multicolinearidade sem reduzir a qualidade geral do modelo de regressão.
Para testar isso, podemos executar a análise de regressão novamente usando apenas peso e mpg como variáveis explicativas:
preço de regressão peso mpg
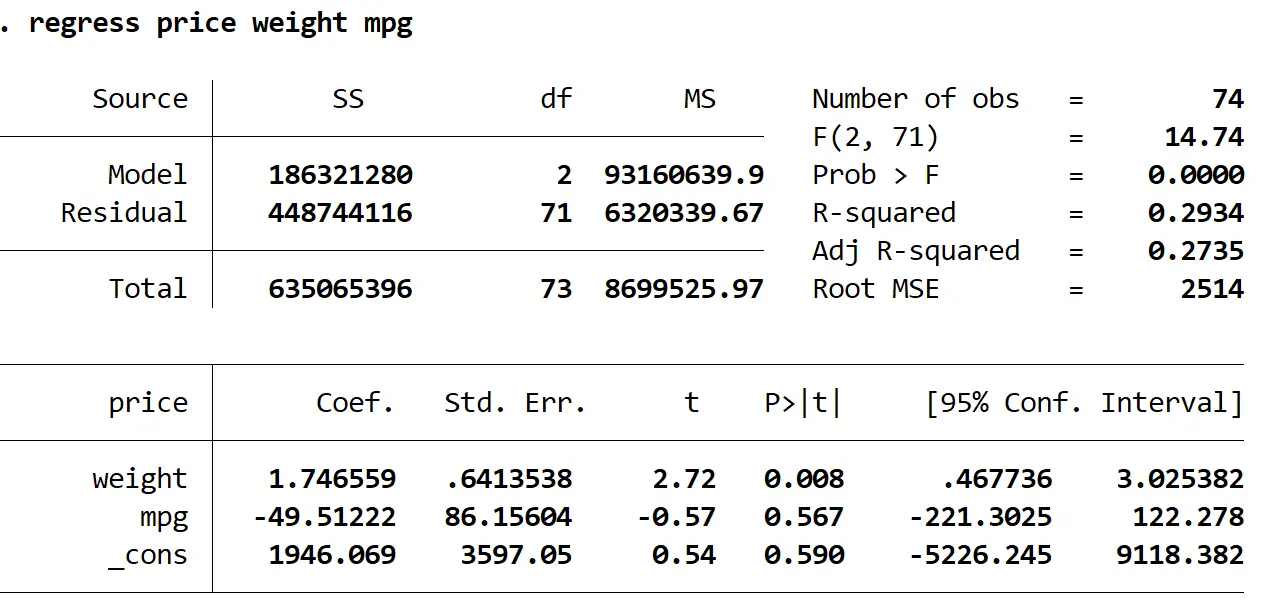
Podemos ver que o R-quadrado ajustado deste modelo é 0,2735 em comparação com 0,3298 no modelo anterior. Isto indica que a utilidade global do modelo diminuiu apenas ligeiramente. Então podemos encontrar os valores VIF usando o comando VIF :
VIVAZ
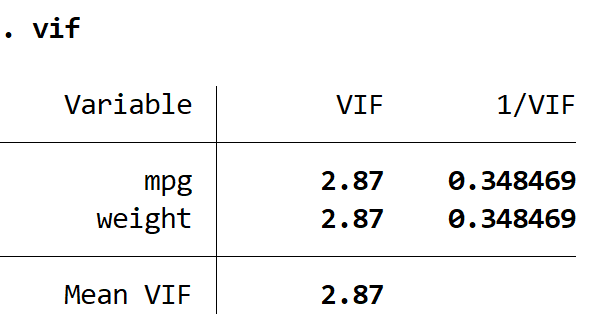
Ambos os valores VIF são inferiores a 5, indicando que a multicolinearidade não é mais um problema no modelo.