Como realizar um teste u de mann-whitney no excel

Um teste U de Mann-Whitney (às vezes chamado de teste de soma de postos de Wilcoxon) é usado para comparar diferenças entre duas amostras quando as distribuições amostrais não são normalmente distribuídas e os tamanhos das amostras são pequenos (n <30).

É considerado o equivalente não paramétrico do teste t para duas amostras .

Este tutorial explica como realizar um teste U de Mann-Whitney no Excel.

Exemplo: teste U de Mann-Whitney no Excel

Os pesquisadores querem saber se o tratamento do combustível causa uma alteração no consumo médio de mpg de um carro. Para testar isso, eles realizam um experimento no qual medem o mpg de 12 carros com tratamento de combustível e 12 carros sem tratamento.

Como os tamanhos amostrais são pequenos e eles suspeitam que as distribuições amostrais não são normalmente distribuídas, eles decidiram realizar um teste U de Mann-Whitney para determinar se há uma diferença estatisticamente significativa em mpg entre os dois grupos.

Conclua as etapas a seguir para realizar um teste U de Mann-Whitney no Excel.

Passo 1: Insira os dados.

Insira os dados da seguinte forma:

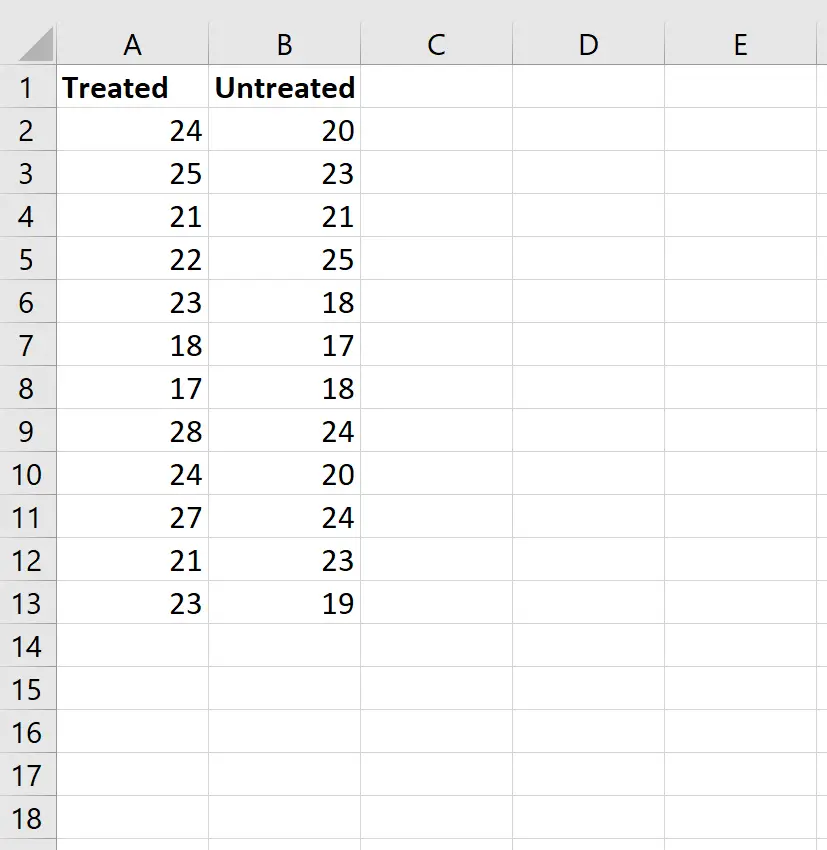
Etapa 2: Calcule as classificações para ambos os grupos.

A seguir, calcularemos as classificações de cada grupo. A imagem a seguir mostra a fórmula a ser usada para calcular a classificação do primeiro valor no grupo Processado:

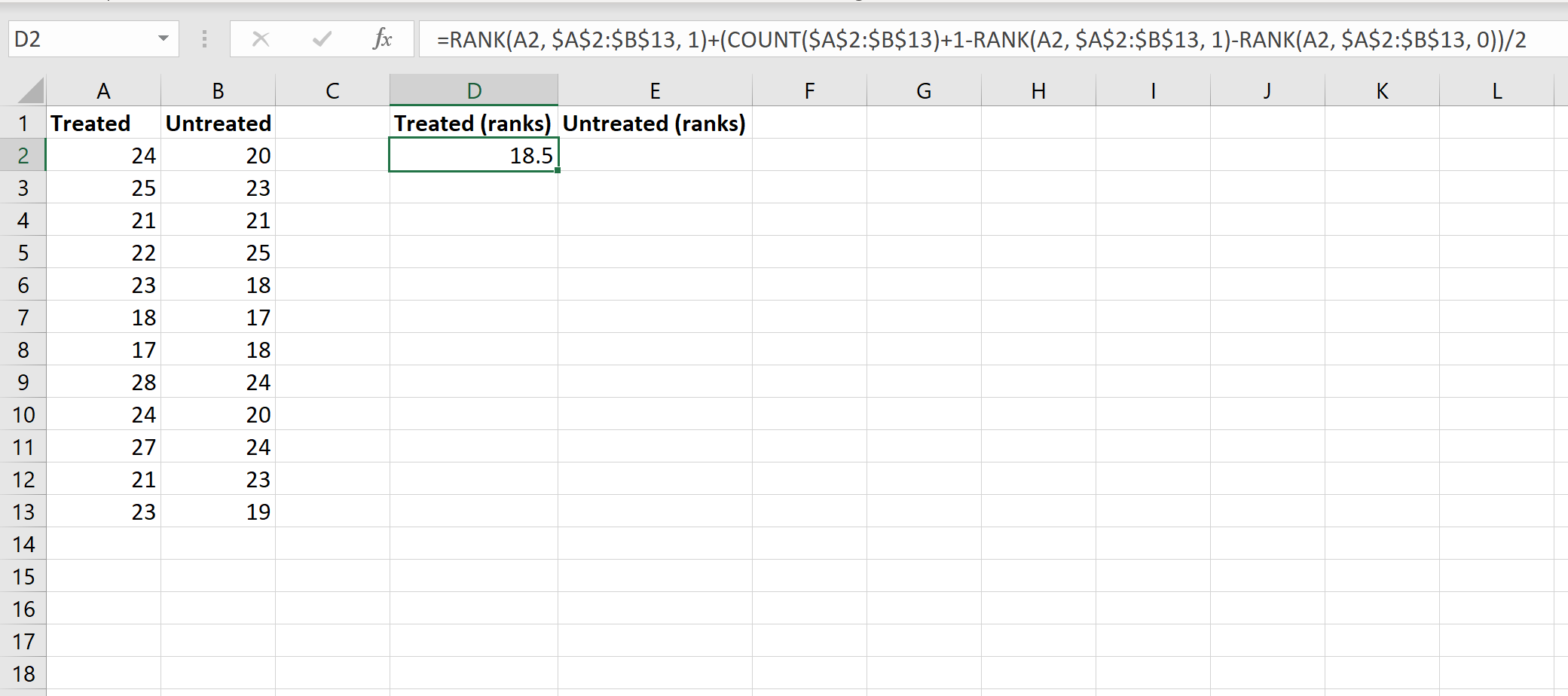
Embora esta fórmula seja bastante complicada, você só precisa inseri-la uma vez. Depois, você pode simplesmente arrastar a fórmula para todas as outras células para preencher as linhas:

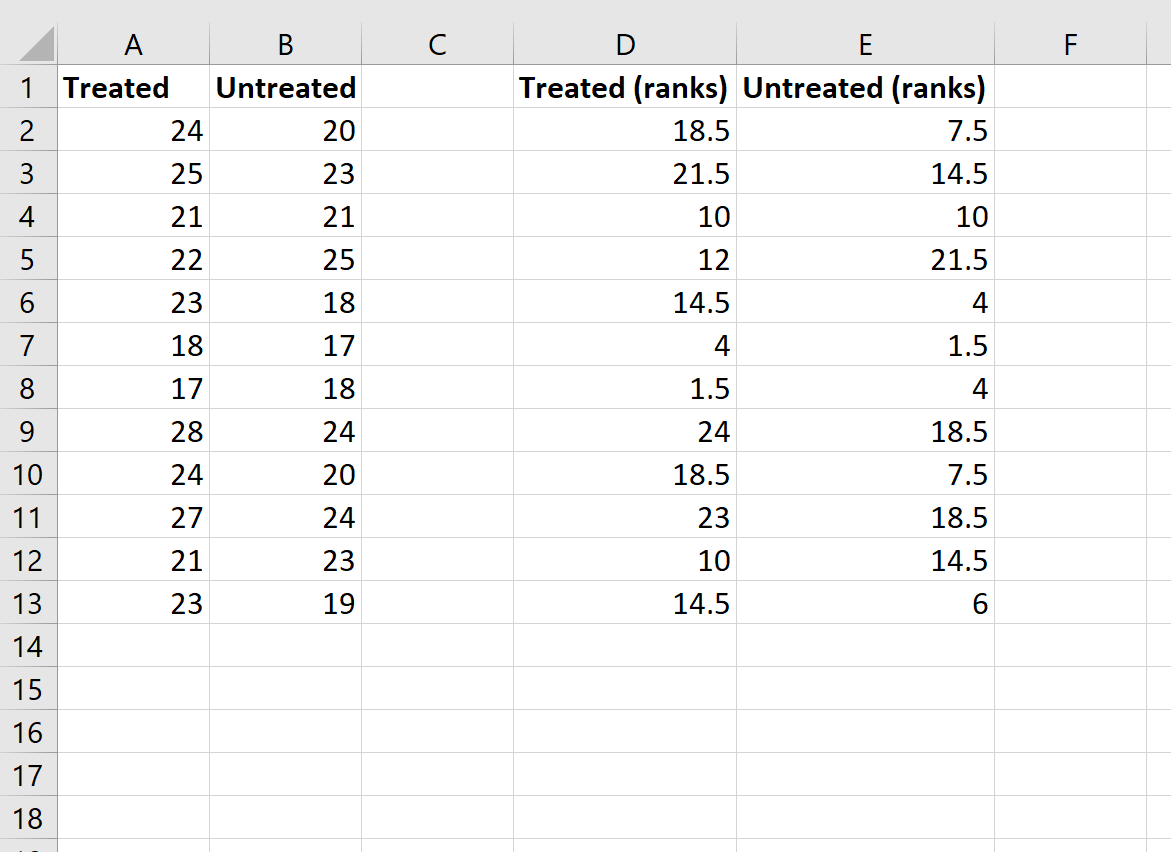
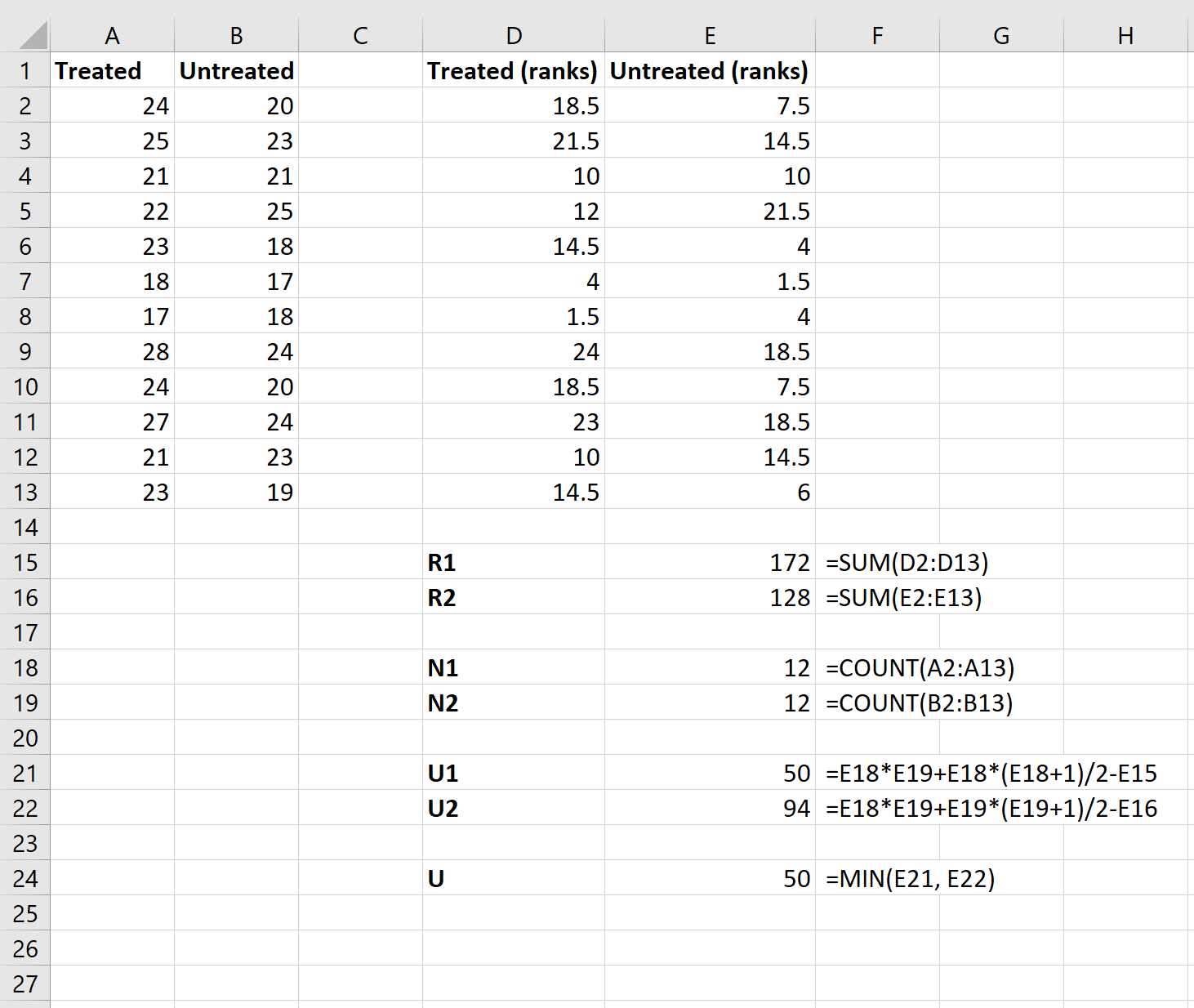
Etapa 3: Calcule os valores necessários para a estatística de teste.

A seguir, usaremos as seguintes fórmulas para calcular a soma das classificações de cada grupo, o tamanho da amostra para cada grupo, a estatística do teste U para cada grupo e a estatística geral do teste U:

Etapa 4: Calcule a estatística do teste z e o valor p correspondente.

Finalmente, usaremos as seguintes fórmulas para calcular a estatística do teste z e o valor p correspondente para determinar se devemos ou não rejeitar a hipótese nula:

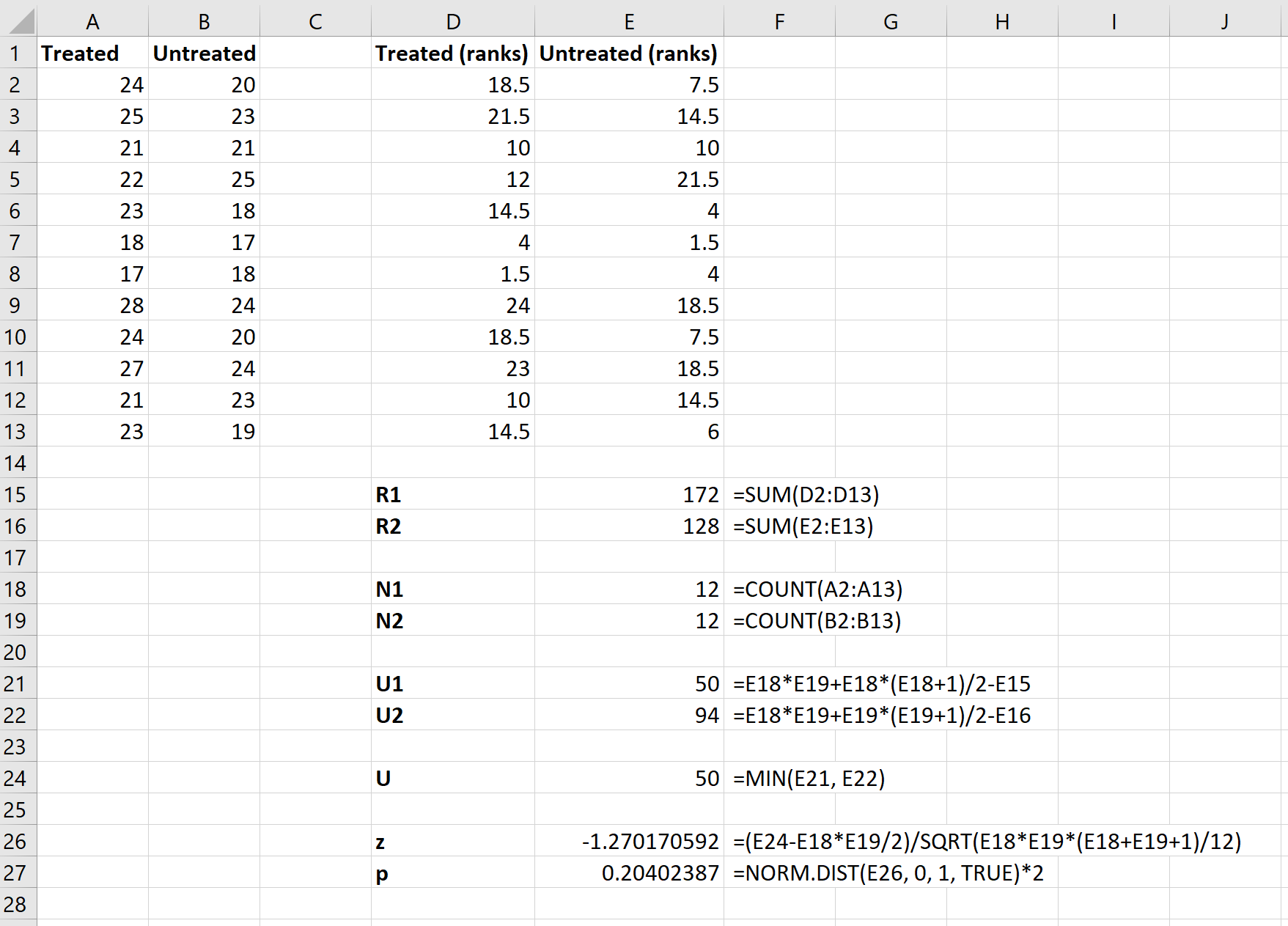
A hipótese nula do teste afirma que ambos os grupos têm o mesmo mpg médio. Como o valor p do teste ( 0,20402387 ) não é inferior ao nosso nível de significância de 0,05, não conseguimos rejeitar a hipótese nula.

Não temos evidências suficientes para dizer que a verdadeira média de mpg é diferente entre os dois grupos.