Como criar e interpretar uma matriz de correlação no excel

Uma forma de quantificar a relação entre duas variáveis é utilizar o coeficiente de correlação de Pearson , que é uma medida da associação linear entre duas variáveis .

Tem um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

Quanto mais longe o coeficiente de correlação estiver de zero, mais forte será a relação entre as duas variáveis.

Mas, em alguns casos, queremos compreender a correlação entre múltiplos pares de variáveis.

Nestes casos, podemos criar uma matriz de correlação , que é uma tabela quadrada que mostra os coeficientes de correlação entre várias combinações de variáveis aos pares.

Este tutorial explica como criar e interpretar uma matriz de correlação no Excel.

Como criar uma matriz de correlação no Excel

Digamos que temos o seguinte conjunto de dados que mostra o número médio de pontos, rebotes e assistências de 10 jogadores de basquete:

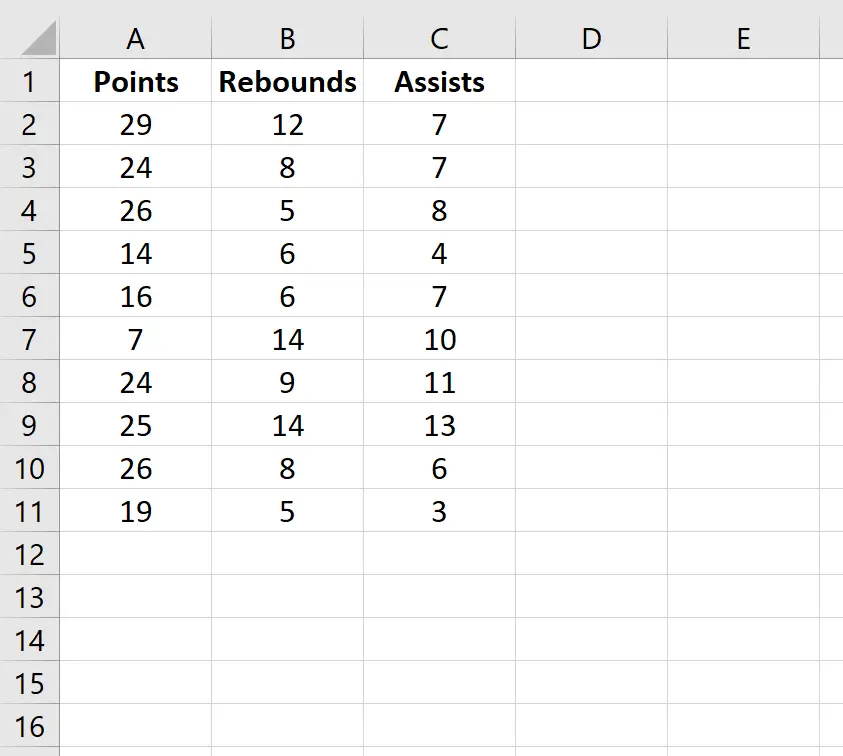
Para criar uma matriz de correlação para este conjunto de dados, vá para a guia Dados na faixa superior do Excel e clique em Análise de Dados .

Se você não vir esta opção, primeiro você deve carregar o Data Analysis Toolpak gratuito no Excel .

Na nova janela que aparece, selecione Correlação e clique em OK .

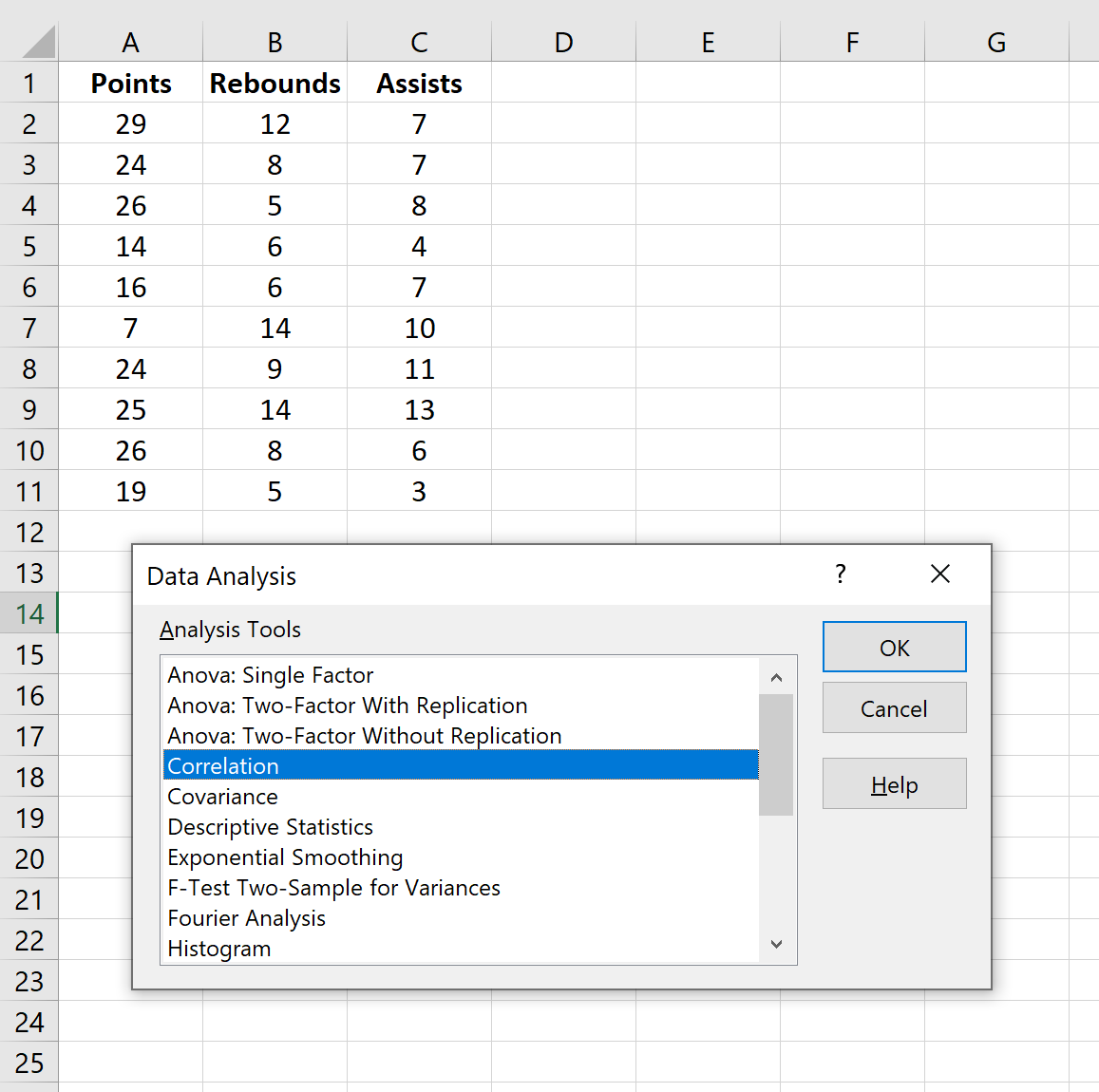
Para Intervalo de entrada , selecione as células onde os dados estão localizados (incluindo a primeira linha com rótulos). Marque a caixa ao lado de Rótulos na primeira linha . Para Intervalo de saída , selecione uma célula onde deseja que a matriz de correlação apareça. Em seguida, clique em OK .

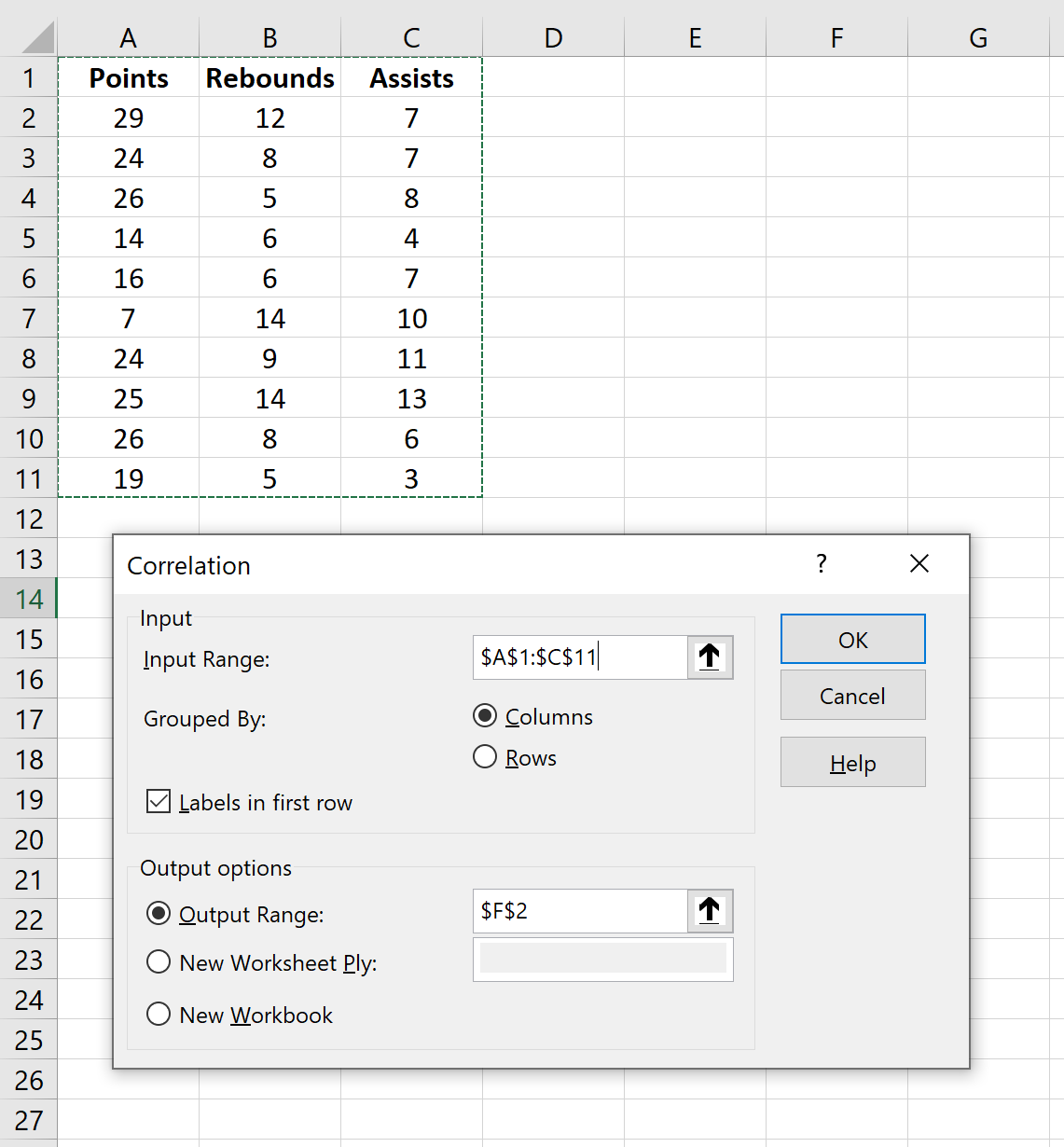
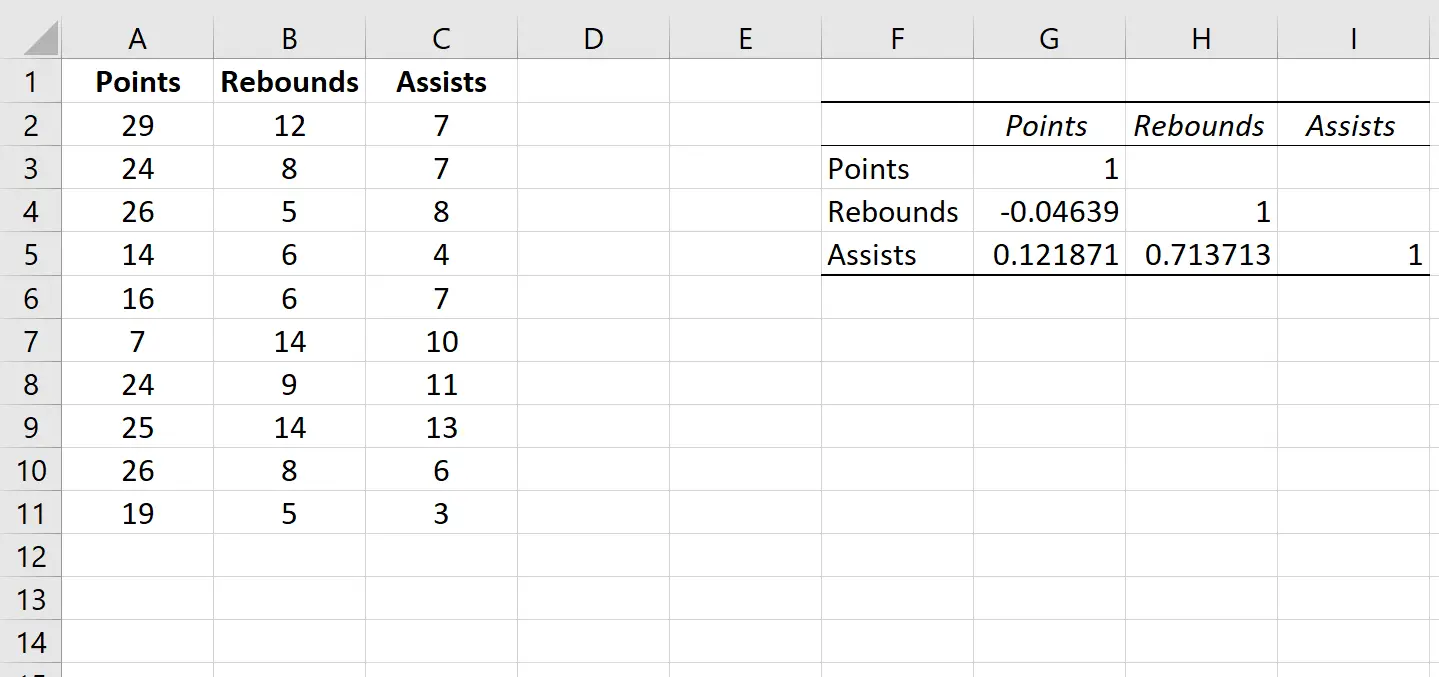
Isso produzirá automaticamente a seguinte matriz de correlação:

Como interpretar uma matriz de correlação no Excel

Os valores nas células individuais da matriz de correlação nos informam o coeficiente de correlação de Pearson entre cada combinação de variáveis aos pares. Por exemplo:

Correlação entre pontos e rebotes: -0,04639. Os pontos e os rebotes estão ligeiramente correlacionados negativamente, mas esse valor é tão próximo de zero que não há fortes evidências de uma associação significativa entre essas duas variáveis.

Correlação entre pontos e assistências: 0,121871. Os pontos e assistências estão ligeiramente correlacionados positivamente, mas este valor também é bastante próximo de zero, pelo que não há fortes evidências de uma associação significativa entre estas duas variáveis.

Correlação entre rebotes e assistências: 0,713713. Rebotes e assistências estão fortemente correlacionados positivamente. Ou seja, jogadores que têm mais rebotes também tendem a dar mais assistências.

Observe que os valores diagonais da matriz de correlação são todos 1 porque a correlação entre uma variável e ela mesma é sempre 1. Na prática, esse número não é útil para interpretação.

Bônus: visualize os coeficientes de correlação

Uma maneira simples de visualizar o valor dos coeficientes de correlação na tabela é aplicar formatação condicional à tabela.

Na faixa superior do Excel, vá para a guia Início e depois para o grupo Estilos .

Clique em Gráfico de formatação condicional , em Escalas de cores e em Escala de cores verde-amarelo-vermelho .

Isso aplica automaticamente a seguinte escala de cores à matriz de correlação:

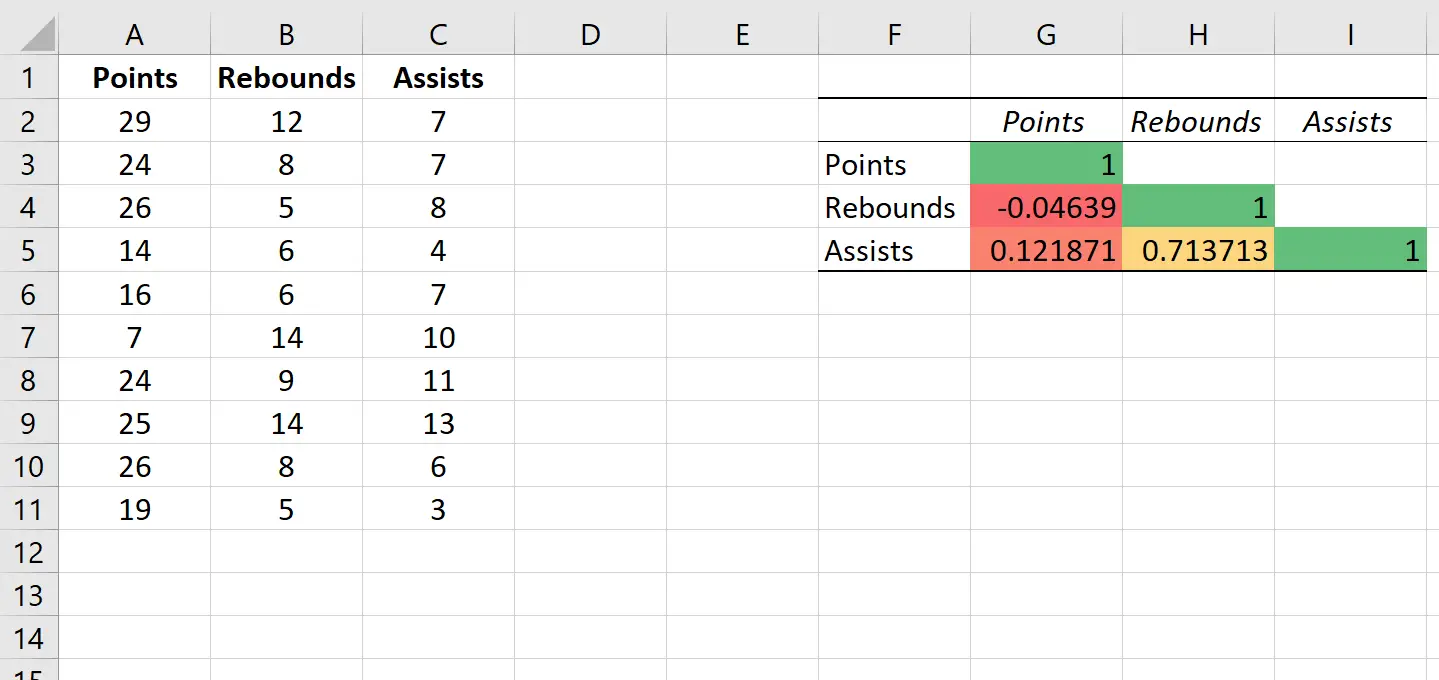
Isso nos ajuda a visualizar facilmente a força das correlações entre as variáveis.

Esta é uma dica especialmente útil se estivermos trabalhando com uma matriz de correlação com muitas variáveis, pois nos ajuda a identificar rapidamente as variáveis que possuem as correlações mais fortes.

Relacionado: O que é considerado uma correlação “forte”?

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras tarefas comuns em R:

Como criar uma matriz de gráfico de dispersão no Excel
Como realizar um teste de correlação no Excel