Como calcular a correlação de classificação de spearman no excel
Nas estatísticas, a correlação refere-se à força e à direção de uma relação entre duas variáveis. O valor de um coeficiente de correlação pode variar de -1 a 1, com as seguintes interpretações:
- -1: uma relação negativa perfeita entre duas variáveis
- 0: nenhuma relação entre duas variáveis
- 1: uma relação positiva perfeita entre duas variáveis
Um tipo especial de correlação é chamado de correlação de classificação de Spearman , que é usada para medir a correlação entre duas variáveis classificadas. (por exemplo, a classificação da pontuação no exame de matemática de um aluno em relação à classificação da pontuação no exame de ciências em uma turma).
Este tutorial explica como calcular a correlação de classificação de Spearman entre duas variáveis no Excel.
Exemplo: correlação de classificação de Spearman no Excel
Execute as etapas a seguir para calcular a correlação de classificação de Spearman entre a pontuação do exame de matemática e a pontuação do exame de ciências de 10 alunos em uma turma específica.
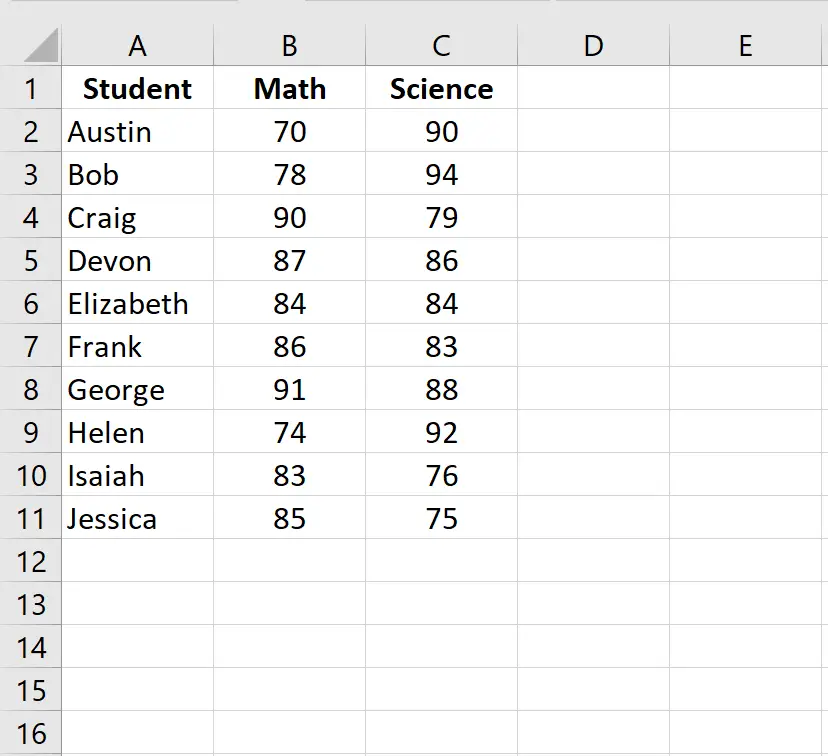
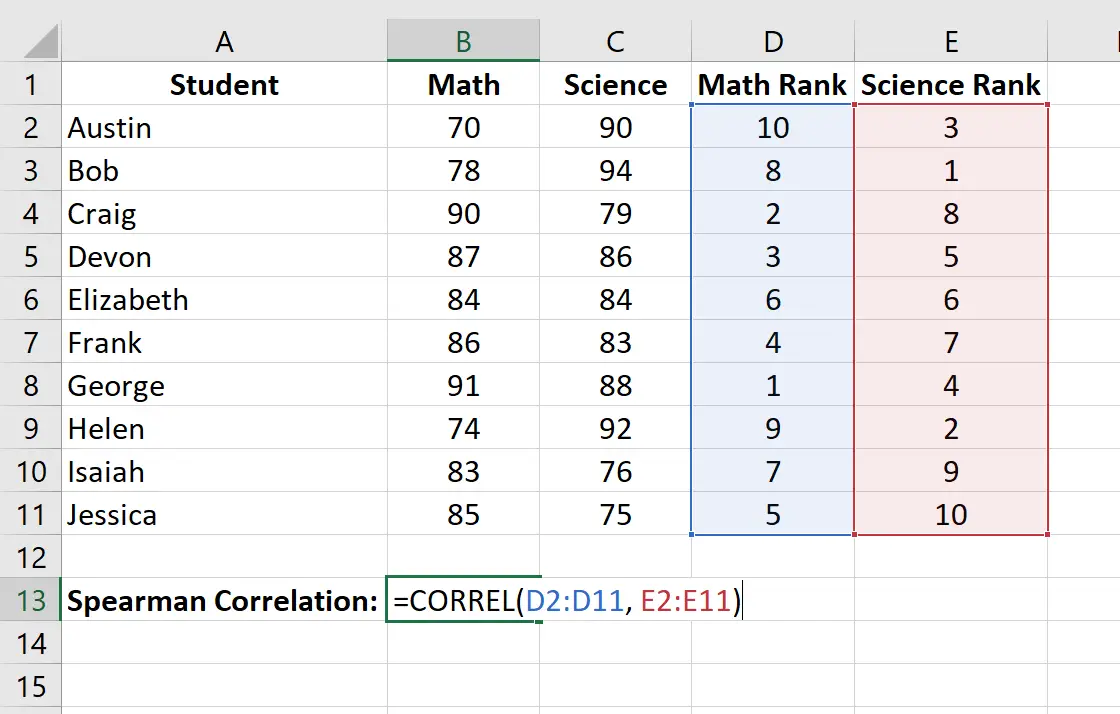
Passo 1: Insira os dados.
Insira os resultados do exame de cada aluno em duas colunas separadas:
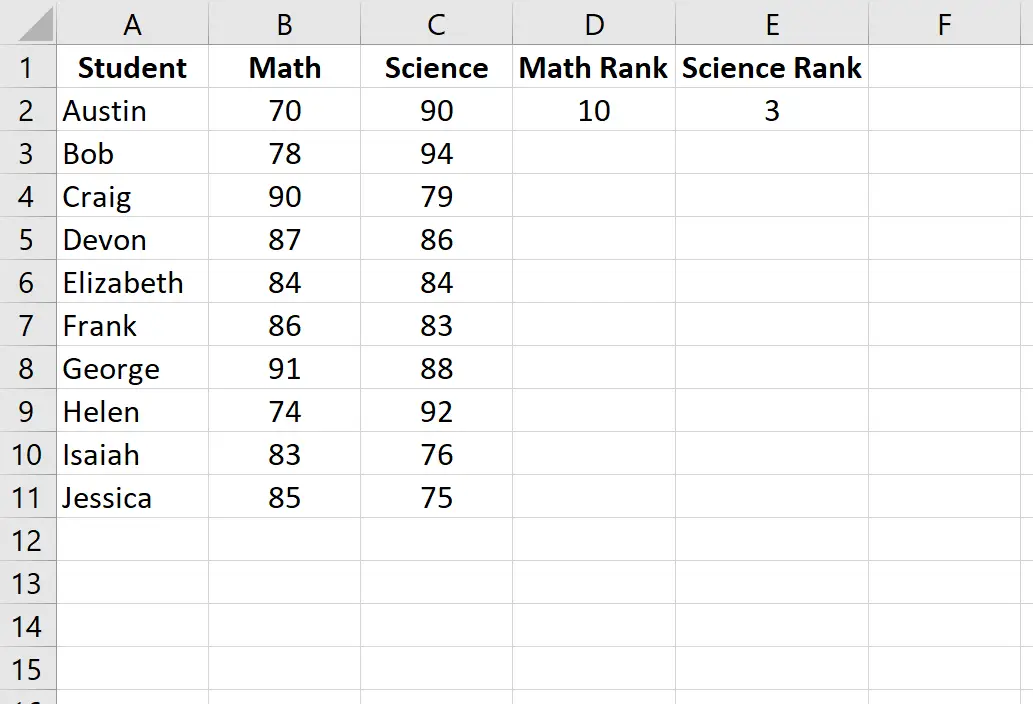
Etapa 2: Calcule as classificações para cada pontuação do exame.
A seguir, calcularemos a classificação de cada nota do exame. Use as seguintes fórmulas nas células D2 e E2 para calcular as classificações de matemática e ciências do primeiro aluno, Austin:
Célula D2: =RANK.AVG(B2, $B$2:$B$11, 0)
Célula E2: =RANK.AVG(C2, $C$2:$C$11, 0)
A seguir, destaque as células restantes para preencher:
Em seguida, clique em Ctrl+D para inserir as classificações de cada aluno:
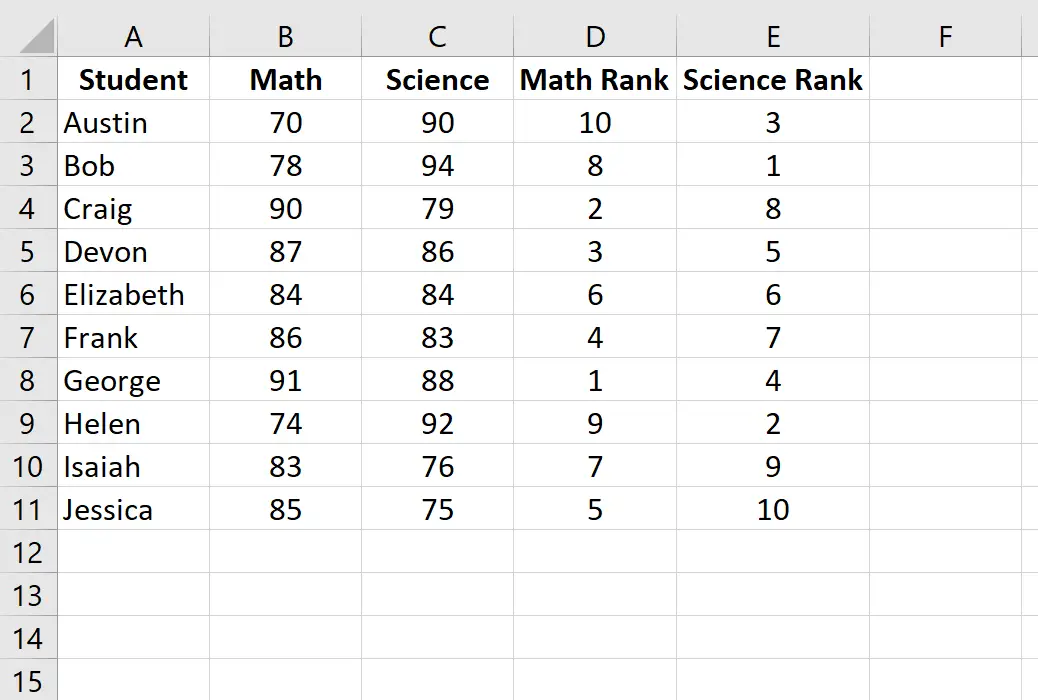
Etapa 3: Calcule o coeficiente de correlação de classificação de Spearman.
Finalmente, calcularemos o coeficiente de correlação de classificação de Spearman entre as pontuações em matemática e as pontuações em ciências usando a função CORREL() :
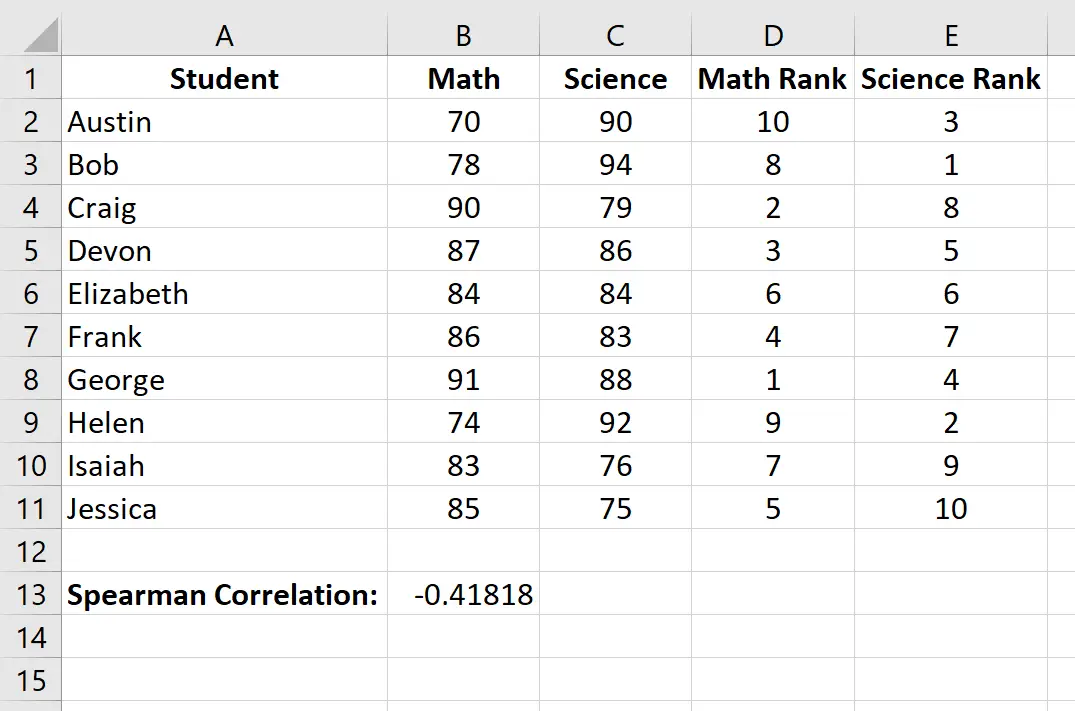
A correlação de classificação de Spearman é -0,41818 .
Etapa 4 (opcional): determine se a correlação de classificação de Spearman é estatisticamente significativa.
Na etapa anterior, descobrimos que a correlação de Spearman entre as notas dos exames de matemática e ciências foi de -0,41818 , indicando uma correlação negativa entre as duas variáveis.
No entanto, para determinar se esta correlação é estatisticamente significativa, precisaríamos nos referir a uma tabela de correlação de valores críticos de Spearman, que mostra os valores críticos associados a diferentes tamanhos de amostra (n) e níveis de significância (α).
Se o valor absoluto do nosso coeficiente de correlação for maior que o valor crítico da tabela, então a correlação entre as duas variáveis é estatisticamente significativa.
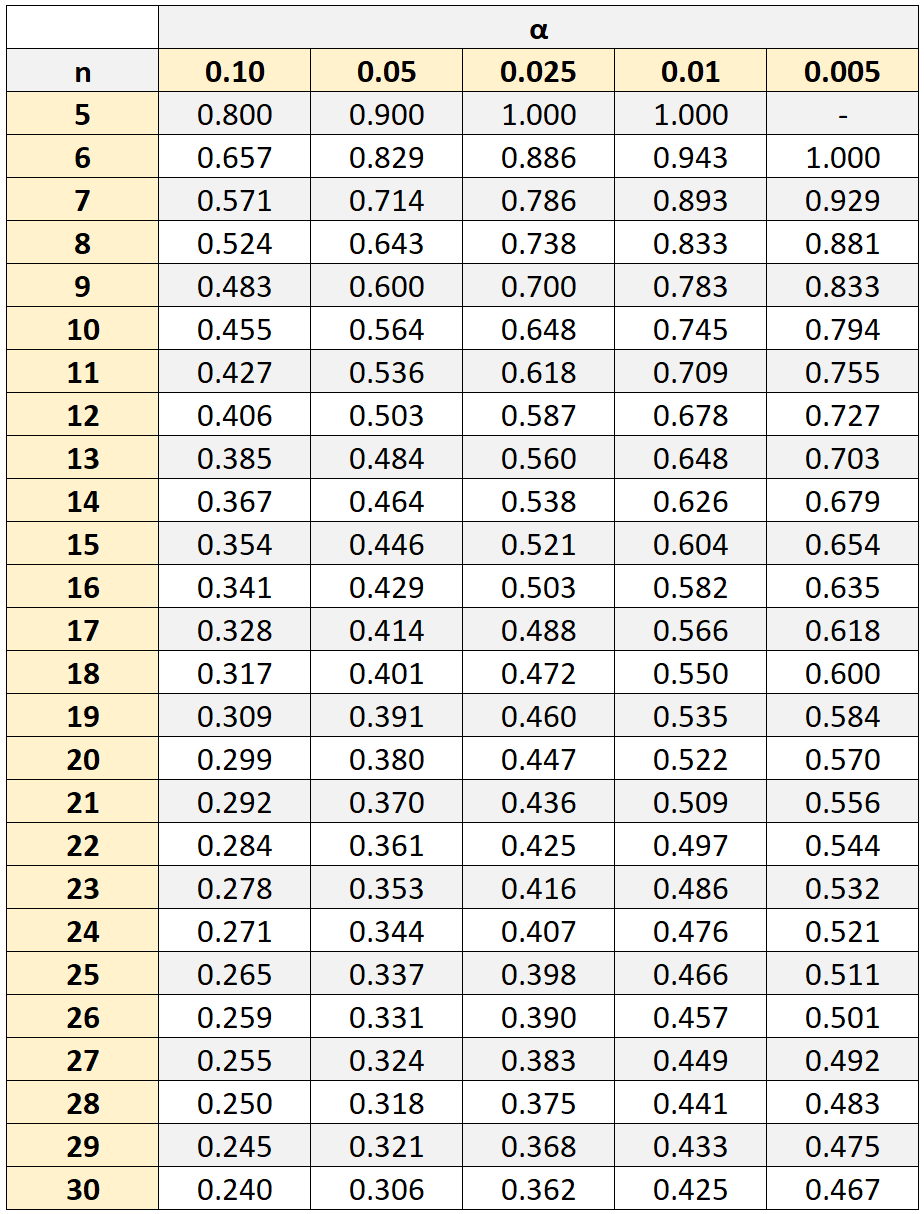
Em nosso exemplo, nosso tamanho de amostra foi n = 10 alunos. Utilizando um nível de significância de 0,05, descobrimos que o valor crítico é 0,564 .
Como o valor absoluto do coeficiente de correlação de classificação de Spearman que calculamos ( 0,41818 ) não é maior que esse valor crítico, isso significa que a correlação entre as pontuações em matemática e ciências não é estatisticamente significativa.