Variância
Neste artigo explicamos o que é a variância, também chamada de variância e como ela é calculada. Você encontrará a fórmula de variância, um exemplo concreto de cálculo de variância e, além disso, poderá calcular a variância de qualquer conjunto de dados com uma calculadora online.
Também mostramos como encontrar a variância de dados agrupados, pois isso é feito de uma forma diferente. Por fim, ensinamos a diferença entre variância populacional e variância amostral, a diferença entre variância e desvio padrão e as propriedades desta medida estatística.
O que é variação?
Nas estatísticas, a variância é uma medida de dispersão que indica a variabilidade de uma variável aleatória. A variância é igual à soma dos quadrados dos resíduos dividida pelo número total de observações.
Lembre-se de que o resíduo é entendido como a diferença entre o valor de um dado estatístico e a média do conjunto de dados.
Na teoria das probabilidades, o símbolo da variância é a letra grega sigma ao quadrado (σ 2 ). Embora também seja geralmente representado como Var(X) , sendo X a variável aleatória a partir da qual a variância é calculada.
Em geral, interpretar o valor da variância de uma variável aleatória é simples. Quanto maior o valor da variância, mais dispersos serão os dados. E vice-versa, quanto menor o valor da variância, menor será a dispersão na série de dados. Porém, ao interpretar a variância, deve-se ter cuidado com valores discrepantes , pois eles podem distorcer o valor da variância.
variância, outras medidas consideradas além de dispersão são amplitude, desvio padrão, desvio médio e coeficiente de variação.
Como calcular a lacuna
Para calcular a variância, as seguintes etapas devem ser executadas:
- Encontre a média aritmética do conjunto de dados.
- Calcule os resíduos, definidos como a diferença entre os valores e a média do conjunto de dados.
- Eleve ao quadrado cada resto.
- Adicione todos os resultados calculados na etapa anterior.
- Divida pelo número total de dados. O resultado obtido é a variância da série de dados.
Concluindo, a fórmula para calcular a variância de um conjunto de dados é:

Ouro:
-

é a variável aleatória para a qual você deseja calcular a variância.
-

é o valor dos dados

.
-

é o número total de observações.
-

é a média da variável aleatória

.
👉 Você pode usar a calculadora abaixo para calcular a variação de qualquer conjunto de dados.
Portanto, para extrair a variância de uma série de dados, é fundamental que você saiba como é calculada a média aritmética. Se você não se lembra de como fazer isso, pode conferir no artigo com link acima.
Exemplo de desvio
Agora que conhecemos a definição de variância, resolveremos passo a passo um exercício para que você possa ver como é obtida a variância de uma série de dados.
- De uma empresa multinacional é conhecido o resultado económico que teve nos últimos cinco anos, na sua maioria obteve lucros mas num ano apresentou perdas consideráveis: 11,5, 2, -9, 7 milhões de euros. Calcule a variância deste conjunto de dados.
Como vimos na explicação acima, a primeira coisa que precisamos fazer para encontrar a variância de uma série de dados é calcular a sua média aritmética:
![]()
E uma vez que sabemos o valor médio dos dados, podemos usar a fórmula de variância:

Substituímos os dados fornecidos pela declaração de exercício na fórmula:
![]()
Por fim, resta resolver as operações para calcular a variância:
![Rendered by QuickLaTeX.com \begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c2cbee60d77f19e88117e1bcf28d9cb2_l3.png)
Note-se que as unidades de variância são as mesmas unidades dos dados estatísticos mas ao quadrado, por esta razão a variância deste grupo de dados é de 45,76 milhões de euros 2 .
Calculadora de lacuna
Insira um conjunto de dados estatísticos na calculadora a seguir para calcular sua variação. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.
Variação para dados agrupados
Para calcular a variância dos dados agrupados em intervalos , devem ser seguidos os seguintes passos:
- Encontre a média dos dados agrupados.
- Calcule os resíduos dos dados agrupados.
- Eleve ao quadrado cada resto.
- Multiplique cada resultado anterior pela frequência de seu intervalo.
- Some a soma de todos os valores obtidos na etapa anterior.
- Divida pelo número total de observações. O número resultante é a variação dos dados agrupados.
Em outras palavras, a fórmula para cálculo da variância dos dados agrupados em intervalos é a seguinte:
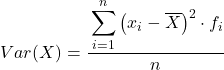
Embora a fórmula acima seja normalmente usada, a expressão algébrica abaixo também pode ser usada por ser equivalente:
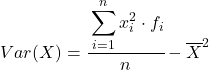
Como exemplo, encontraremos a variância das seguintes séries de dados agrupados:
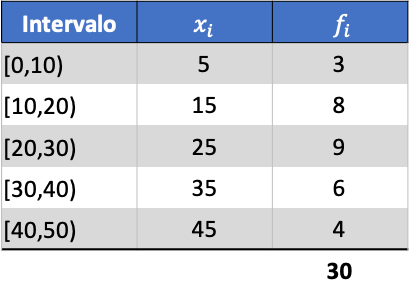
Primeiro, precisamos determinar a média dos dados agrupados. Para isso, adicionamos uma coluna na tabela de frequência com o produto da marca da classe pela frequência:
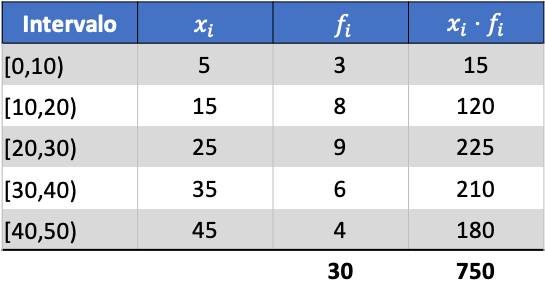
Calculamos agora a média dos dados agrupados dividindo a soma da coluna adicionada pelo número total de dados:
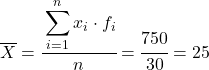
E a partir da média dos dados calculados, podemos adicionar as três colunas a seguir:
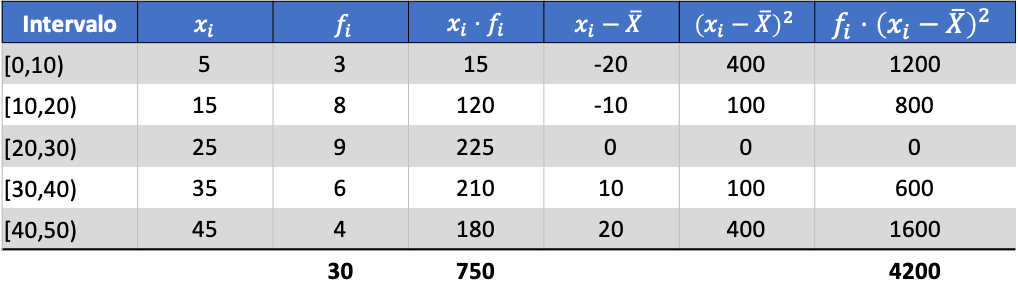
Portanto, a variância do conjunto de dados agrupados é a soma da última coluna dividida pelo número total de dados observados:
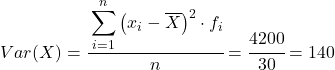
Variância e desvio padrão
A variância e o desvio padrão (ou desvio padrão) são duas medidas de dispersão e, portanto, ambas indicam o grau de dispersão do conjunto de dados. Porém, a diferença entre a variância e o desvio padrão é que em geral a variância possui valores maiores, pois é o quadrado do desvio padrão.
O desvio padrão é geralmente representado pela letra grega sigma (σ), e por esta razão a variância é representada pela letra sigma ao quadrado (σ 2 ), pois é a relação matemática que existe entre estas duas métricas de dispersão.
![]()
Assim, depois de calcular o valor da variância de um conjunto de dados, você pode facilmente encontrar o valor do desvio padrão desse mesmo conjunto simplesmente calculando a raiz quadrada da variância.
![]()
Variância populacional e variância amostral
Logicamente, a variância populacional refere-se ao cálculo da variância de uma população estatística e, em vez disso, a variância amostral é aplicada ao cálculo da variância de uma amostra. No entanto, estes são dois conceitos diferentes, uma vez que a fórmula de variância populacional é diferente da fórmula de variância amostral.
Normalmente em exercícios de variância, se não nos disserem o contrário, para encontrar a variância do conjunto de dados fornecido temos que usar a fórmula de variância populacional , que é a que explicamos no início do artigo:
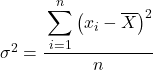
Mas talvez em alguns problemas você seja solicitado a tratar os dados estatísticos como uma amostra; nesse caso, precisamos usar a fórmula de variância amostral :
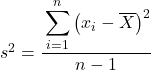
Observe que para indicar que uma variância populacional está sendo calculada, ela é indicada pela letra grega σ, mas quando uma variância amostral está sendo calculada, a letra s é usada.
Como você pode ver, a única diferença entre as duas fórmulas é que na variância de uma amostra precisamos dividir pelo número total de observações menos 1, por exemplo, se houver 30 itens de dados no total, dividiremos por 29 Mas o cálculo do numerador é feito exatamente da mesma maneira.
Propriedades de variação
A variação tem as seguintes propriedades:
- A variância de qualquer variável aleatória será sempre maior ou igual a zero. Da mesma forma, se a variância for zero, significa que todos os dados estatísticos são iguais.
![]()
- Obviamente, a variância de um único valor é zero.
![]()
- A variância do produto de um escalar por uma variável é equivalente a esse escalar ao quadrado vezes a variância da variável.
![]()
- A variância da soma de duas variáveis dependentes é equivalente à soma da variância de cada variável separadamente mais o dobro da covariância entre as duas variáveis.
![]()
- Consequentemente, se as duas variáveis são independentes, para determinar a variância da sua soma basta somar as suas variâncias:
![]()
- O desvio também pode ser definido com a expectativa matemática utilizando a seguinte fórmula:
![]()