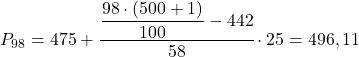Percentis (estatísticas)
Este artigo explica o que é um percentil e como ele é calculado. Você encontrará exercícios de percentis resolvidos e, além disso, poderá calcular qualquer percentil da sua amostra de dados com uma calculadora online.
O que são percentis?
Nas estatísticas, os percentis são os valores que dividem um conjunto de dados ordenados em cem partes iguais. Portanto, um percentil indica o valor abaixo do qual cai uma porcentagem do conjunto de dados.
Por exemplo, o valor do percentil 35 é superior a 35% dos dados observados, mas inferior ao restante dos dados.
Os percentis são representados pela letra maiúscula P e pelo índice de percentis, ou seja, o 1º percentil é P 1 , o 40º percentil é P 40 , o 79º percentil é P 79 , e assim por diante.

👉 Você pode usar a calculadora abaixo para calcular percentis de qualquer conjunto de dados.
Da mesma forma, os percentis são uma medida da posição não central juntamente com os quartis, quintis e decis. Você pode verificar o significado de cada um desses tipos de quantis em nosso site.
Ressalta-se que o termo percentis também é utilizado para comparar o peso e a altura de um bebê com os valores padrão de outros bebês, pois existem tabelas de crescimento com valores registrados que ajudam a determinar se o bebê está crescendo corretamente ou não. . .
Como calcular percentis
Para calcular a posição de um percentil de uma série de dados estatísticos, você deve multiplicar o número do percentil pela soma do número total de pontos de dados mais um e dividir o resultado por cem.
A fórmula do percentil é, portanto:
![]()
Atenção: esta fórmula indica-nos a posição do percentil, mas não o seu valor. O percentil serão os dados localizados na posição obtida pela fórmula.
Porém, por vezes o resultado desta fórmula nos dará um número decimal, devemos portanto distinguir dois casos dependendo se o resultado é um número decimal ou não:
- Se o resultado da fórmula for um número sem parte decimal , o percentil corresponde ao dado que está na posição fornecida pela fórmula acima.
- Se o resultado da fórmula for um número com parte decimal , o valor exato do percentil é calculado usando a seguinte fórmula:
![]()
Onde x i e x i+1 são os números das posições entre as quais se localiza o número obtido pela primeira fórmula, ed é a parte decimal do número obtido pela primeira fórmula.
Agora você pode pensar que encontrar os percentis de uma amostra estatística ou população é complicado porque o método envolve muitas etapas, mas na verdade é fácil. Leia os dois exemplos concretos a seguir e tenho certeza que você entenderá muito melhor.
Nota : A comunidade científica ainda não está totalmente de acordo sobre como calcular percentis, então você pode encontrar um livro de estatística que explica isso de forma um pouco diferente.
Exemplos de cálculo de percentil
Como você viu acima na explicação de como encontrar os percentis de uma amostra, o cálculo varia dependendo se o resultado da primeira fórmula é decimal ou não. É por isso que a seguir você encontrará dois exemplos resolvidos, um para cada caso.
Exemplo 1
- A partir dos dados mostrados na tabela a seguir, calcule o 1º, 43º e 89º percentis.
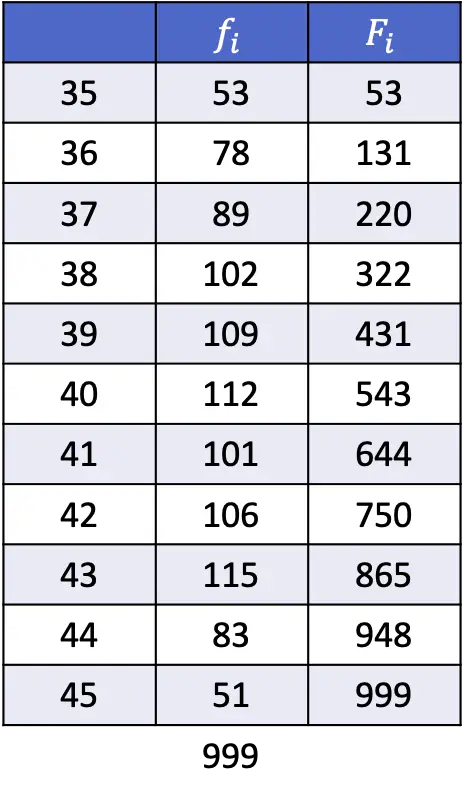
Conforme explicado na seção anterior, a fórmula para encontrar a posição de um percentil é:
![]()
Neste caso, o tamanho da amostra para este exercício é de 999 dados estatísticos, portanto, para calcular a posição do primeiro percentil precisamos substituir 999 por n e 1 por k :
![]()
Assim o 1º percentil será aquele cuja frequência absoluta acumulada for imediatamente superior a 10, que neste caso é 35 pois tem uma frequência absoluta acumulada de 53.
Para determinar o percentil 43 você deve usar a mesma fórmula mas, obviamente, desta vez substituímos o k por 43.
![]()
A frequência acumulada absoluta imediatamente acima de 430 é 431 do dado 39, portanto o percentil 43 é igual a 39.
Por fim, aplicamos a mesma fórmula para obter o percentil 89:
![]()
A frequência absoluta acumulada do valor 44 é 948, que é imediatamente superior a 890. Portanto, o percentil 89 é 44.
Exemplo 2
- Encontre os percentis 35 e 67 das seguintes séries de dados:
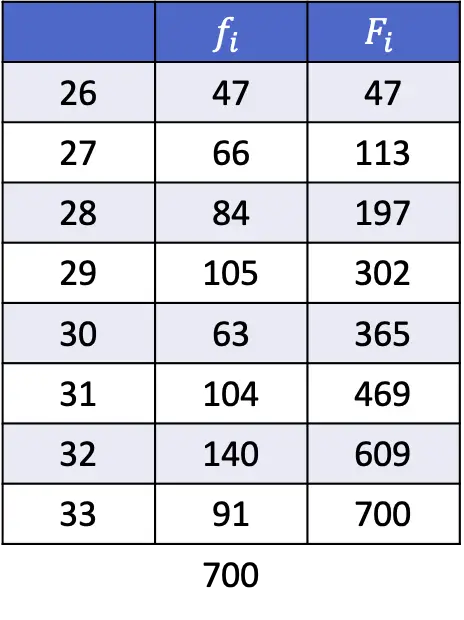
Mesmo que neste exercício tenhamos que fazer mais cálculos, o princípio continua o mesmo: devemos calcular a posição percentual com a seguinte expressão.
![]()
Assim, para calcular o percentil 35 substituímos o k por 35 e o n pelo número total de dados, ou seja, 700:
![]()
Mas desta vez obtivemos um número decimal da fórmula, então precisamos aplicar a seguinte expressão algébrica para calcular o valor exato do percentil:
![]()
O número dado pela primeira fórmula é 245,35, portanto o percentil 35 fica entre as posições 245 e 246, o que corresponde aos valores 29 e 29 respectivamente. Portanto, x i é 29, x i+1 é 29 e d vale a parte decimal do número obtido, ou seja, 0,35.
![]()
Para encontrar o percentil 67, precisamos usar o mesmo método. Primeiro calculamos a posição percentil:
![]()
O número resultante 469,67 indica que o percentil estará entre as posições 469 e 470, cujos valores são 31 e 32. Portanto, usamos a segunda fórmula no processo para encontrar o valor exato do percentil:
![]()
calculadora percentil
Insira um conjunto de dados estatísticos e o número percentil que deseja calcular na calculadora a seguir. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.
Percentis em dados agrupados
Para calcular percentis quando os dados são agrupados em grupos , primeiro precisamos encontrar o grupo ou classe em que o percentil se enquadra usando a seguinte fórmula:
![]()
O percentil estará portanto no intervalo cuja frequência absoluta é imediatamente maior que o número obtido na expressão anterior.
E uma vez que já sabemos a que intervalo pertence o percentil, devemos aplicar a seguinte fórmula para encontrar o valor exato do percentil:
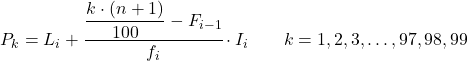
Ouro:
- L i é o limite inferior do intervalo em que se encontra o percentil.
- n é o número total de observações.
- F i-1 é a frequência absoluta acumulada do intervalo anterior.
- f i é a frequência absoluta do intervalo em que se encontra o percentil.
- I i é a largura do intervalo percentil.
Abaixo está um exercício passo a passo sobre como obter percentis quando os dados são expressos em intervalos. Especificamente, são calculados os percentis 29, 52 e 98.

Os dados nesta amostra são agrupados como intervalos, portanto, precisamos realizar duas etapas para determinar os percentis: primeiro, precisamos encontrar o intervalo em que o percentil se enquadra e, em seguida, aplicar a fórmula para calcular o valor exato do percentil. percentil.
Assim, encontramos a posição do percentil 29 com a seguinte expressão:
![]()
![]()
O intervalo percentil será aquele cuja frequência absoluta acumulada for imediatamente superior a 145,29, que neste caso é o intervalo [350,375) cuja frequência absoluta acumulada é 175. E uma vez conhecido o intervalo percentil, aplicamos a seguinte fórmula para calcular seu valor exato:
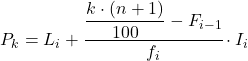
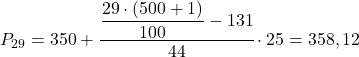
Agora repetimos o mesmo procedimento para calcular o percentil 52. Primeiro calculamos seu intervalo:
![]()
O intervalo do percentil 52 é [400,425), pois sua frequência absoluta acumulada (298) é a imediatamente superior a 260,52. O valor exato do percentil será, portanto:
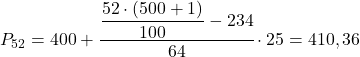
Finalmente, encontraremos o percentil 98. Como sempre, primeiro calculamos o intervalo onde ele se encontra:
![]()
E uma vez conhecido o intervalo onde se encontra o percentil, calculamos seu valor exato com a seguinte fórmula: