Uma introdução à distribuição binomial

A distribuição binomial é uma das distribuições mais populares em estatística. Para entender a distribuição binomial, é útil primeiro entender os experimentos binomiais .

Experimentos binomiais

Um experimento binomial é um experimento que possui as seguintes propriedades:

• O experimento consiste em n tentativas repetidas.
• Cada tentativa tem apenas dois resultados possíveis.
• A probabilidade de sucesso, denotada por p , é a mesma para cada tentativa.
• Cada teste é independente.

O exemplo mais óbvio de um experimento binomial é o lançamento de uma moeda. Por exemplo, digamos que jogamos uma moeda 10 vezes. Este é um experimento binomial porque possui as quatro propriedades a seguir:

• O experimento consiste em n tentativas repetidas – Existem 10 tentativas.
• Cada tentativa tem apenas dois resultados possíveis: cara ou coroa.
• A probabilidade de sucesso, denotada por p , é a mesma para cada tentativa. Se definirmos “sucesso” como acertar cabeças, então a probabilidade de sucesso é exatamente 0,5 para cada tentativa.
• Cada tentativa é independente – O resultado de um lançamento de moeda não afeta o resultado de qualquer outro lançamento de moeda.

A distribuição binomial

A distribuição binomial descreve a probabilidade de obter k sucessos em n experimentos binomiais.

Se uma variável aleatória X segue uma distribuição binomial, então a probabilidade de X = k sucesso pode ser encontrada pela seguinte fórmula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Ouro:

• n: número de tentativas
• k: número de sucessos
• p: probabilidade de sucesso em uma determinada tentativa
• _n C _k : o número de maneiras de obter k sucessos em n tentativas

Por exemplo, suponhamos que jogamos uma moeda 3 vezes. Podemos usar a fórmula acima para determinar a probabilidade de obter 0, 1, 2 e 3 caras nestes 3 lançamentos:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 3 * 0,5 * (0,5) ² = 0,375

P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 3 * 0,25 * (0,5) ¹ = 0,375

P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 0,125 * (0,5) ⁰ = 0,125

Nota : Usamos esta calculadora combinada para calcular _{nCk para} cada exemplo.

Podemos criar um histograma simples para visualizar esta distribuição de probabilidade:

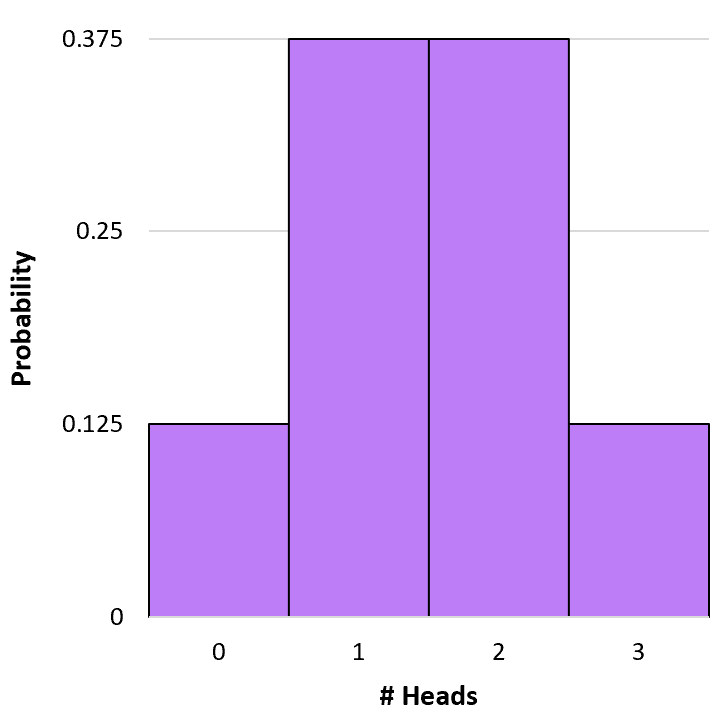
Cálculo de probabilidades binomiais cumulativas

É simples calcular uma única probabilidade binomial (por exemplo, a probabilidade de uma moeda dar cara 1 vez em 3 lançamentos) usando a fórmula acima, mas para calcular probabilidades binomiais cumulativas precisamos adicionar probabilidades individuais.

Por exemplo, digamos que queremos saber a probabilidade de uma moeda dar cara 1 vez ou menos em 3 lançamentos. Usaríamos a seguinte fórmula para calcular essa probabilidade:

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

Isso é chamado de probabilidade cumulativa porque envolve a adição de múltiplas probabilidades. Podemos calcular a probabilidade cumulativa de obter k caras ou menos para cada resultado usando uma fórmula semelhante:

P(X≤0) = P(X=0) = 0,125 .

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .

Podemos criar um histograma para visualizar esta distribuição de probabilidade cumulativa:

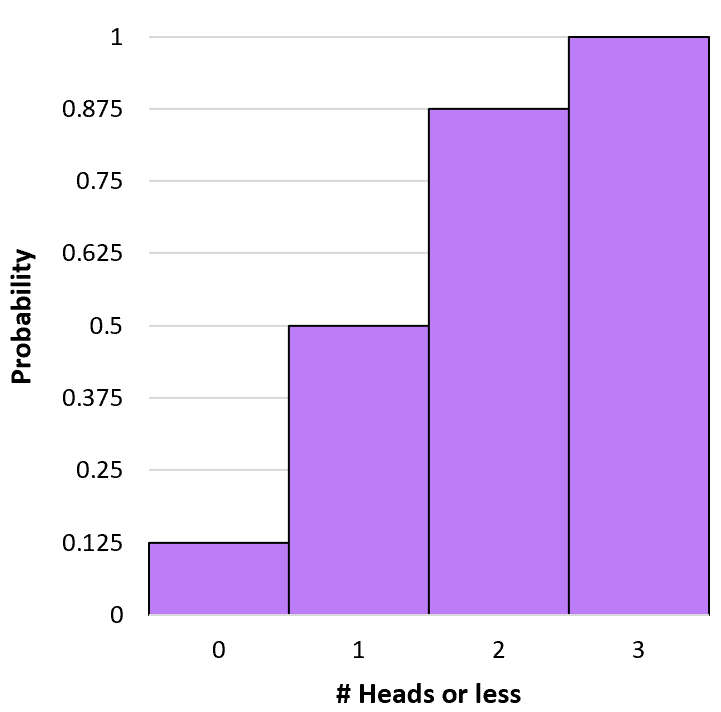
Calculadora de probabilidade binomial

Quando trabalhamos com números pequenos (por exemplo, 3 lançamentos de moeda), é razoável calcular probabilidades binomiais manualmente. Porém, quando trabalhamos com números maiores (por exemplo, 100 sorteios), pode ser difícil calcular as probabilidades manualmente. Nestes casos, pode ser útil usar uma calculadora de probabilidade binomial como a mostrada abaixo.

Por exemplo, suponha que lançamos uma moeda n = 100 vezes, a probabilidade de ela dar cara em uma determinada tentativa é p = 0,5, e queremos saber a probabilidade de ela dar cara k = 43 vezes ou menos:

Veja como interpretar o resultado:

• A probabilidade de a moeda dar cara exatamente 43 vezes é 0,03007 .
• A probabilidade de a moeda dar cara menos de 43 vezes é 0,06661 .
• A probabilidade de a moeda dar cara 43 vezes ou menos é 0,09667 .
• A probabilidade de a moeda dar cara mais de 43 vezes é 0,90333 .
• A probabilidade de a moeda dar cara 43 vezes ou mais é 0,93339 .

Propriedades da distribuição binomial

A distribuição binomial tem as seguintes propriedades:

A média da distribuição é μ = np

A variância da distribuição é σ ² = np(1-p)

O desvio padrão da distribuição é σ = √ np(1-p)

Por exemplo, suponha que joguemos uma moeda 3 vezes. Seja p = a probabilidade de a moeda cair em cara.

O número médio de caras que esperamos é μ = np = 3*.5 = 1.5 .

A variação do número de funcionários que esperamos é σ ² = np(1-p) = 3*.5*(1-.5) = 0.75 .

Problemas práticos de distribuição binomial

Use os seguintes problemas práticos para testar seu conhecimento sobre a distribuição binomial.

Problema 1

Pergunta: Bob acerta 60% de suas tentativas de lance livre. Se ele acertar 12 lances livres, qual é a probabilidade de acertar exatamente 10?

Resposta: Usando a calculadora de distribuição binomial acima com p = 0,6, n = 12 e k = 10, descobrimos que P(X=10) = 0,06385 .

Problema 2

Pergunta: Jéssica joga uma moeda 5 vezes. Qual é a probabilidade de a moeda dar cara 2 vezes ou menos?

Resposta: Usando a calculadora de distribuição binomial acima com p = 0,5, n = 5 e k = 2, descobrimos que P(X≤2) = 0,5 .

Problema 3

Pergunta: A probabilidade de um determinado aluno ser aceito em uma determinada faculdade é de 0,2. Se 10 alunos se inscreverem, qual é a probabilidade de que mais de 4 sejam aceitos?

Resposta: Usando a calculadora de distribuição binomial acima com p = 0,2, n = 10 e k = 4, descobrimos que P(X>4) = 0,03279 .

Problema 4

Pergunta: Você joga uma moeda 12 vezes. Qual é o número médio esperado de caras que aparecerão?

Resposta: Lembre-se de que a média de uma distribuição binomial é calculada como μ = np. Então, μ = 12*0,5 = 6 caras .

Problema 5

Pergunta: Mark acerta um home run em 10% de suas tentativas. Se ele acerta 5 tentativas em um determinado jogo, qual é a variação no número de home runs que ele acerta?

Resposta: Lembre-se de que a variância de uma distribuição binomial é calculada como σ ² = np(1-p). Assim, ^σ2 = 6*.1*(1-.1) = 0,54 .

Recursos adicionais

Os artigos a seguir podem ajudá-lo a aprender como usar a distribuição binomial em diferentes softwares estatísticos:

• Como calcular probabilidades binomiais no Excel
• Como calcular probabilidades binomiais em uma calculadora TI-84
• Como calcular probabilidades binomiais em R
• Como traçar uma distribuição binomial em R