Como aplicar o teorema de chebyshev no excel

O teorema de Chebyshev afirma que para qualquer número k maior que 1, pelo menos 1 – 1/k ² dos valores dos dados em qualquer distribuição treinada está dentro de k desvios padrão da média.

Por exemplo, para qualquer distribuição modelada, pelo menos 1 – 1/3 ² = 88,89% dos valores na distribuição ficarão dentro de 3 desvios padrão da média.

Este tutorial demonstra vários exemplos de aplicação do teorema de Chebyshev no Excel.

Exemplo 1: Use o teorema de Chebyshev para determinar qual porcentagem de valores ficará entre 30 e 70 para um conjunto de dados com média de 50 e desvio padrão de 10.

Primeiro, determine o valor de k. Podemos fazer isso determinando quantos desvios padrão estão entre 30 e 70 da média:

(30 – média) / desvio padrão = (30 – 50) / 10 = -20/10 = -2

(70 – média) / desvio padrão = (70 – 50) / 10 = 20/10 = 2

Os valores 30 e 70 estão 2 desvios padrão abaixo e acima da média, respectivamente. Então, k = 2 .

Podemos então usar a seguinte fórmula no Excel para encontrar a porcentagem mínima de valores que estão dentro de 2 desvios padrão da média deste conjunto de dados:

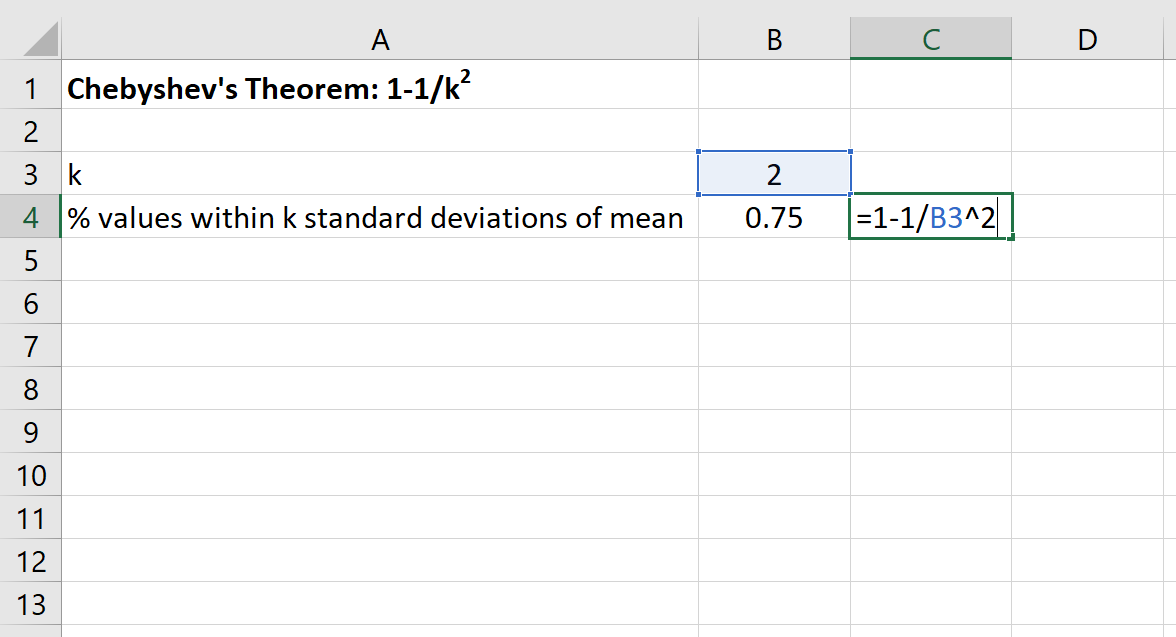
A porcentagem de valores entre 30 e 70 para este conjunto de dados será de pelo menos 75% .

Exemplo 2: Use o teorema de Chebyshev para determinar qual porcentagem de valores ficará entre 20 e 50 para um conjunto de dados com média de 35 e desvio padrão de 5.

Primeiro, determine o valor de k. Podemos fazer isso determinando quantos desvios padrão estão entre 20 e 50 da média:

(20 – média) / desvio padrão = (20 – 35) / 5 = -15/5 = -3

(50 – média) / desvio padrão = (50 – 35) / 5 = 15/5 = 3

Os valores 20 e 50 estão 3 desvios padrão abaixo e acima da média, respectivamente. Então, k = 3 .

Podemos então usar a seguinte fórmula no Excel para encontrar a porcentagem mínima de valores que estão dentro de 3 desvios padrão da média deste conjunto de dados:

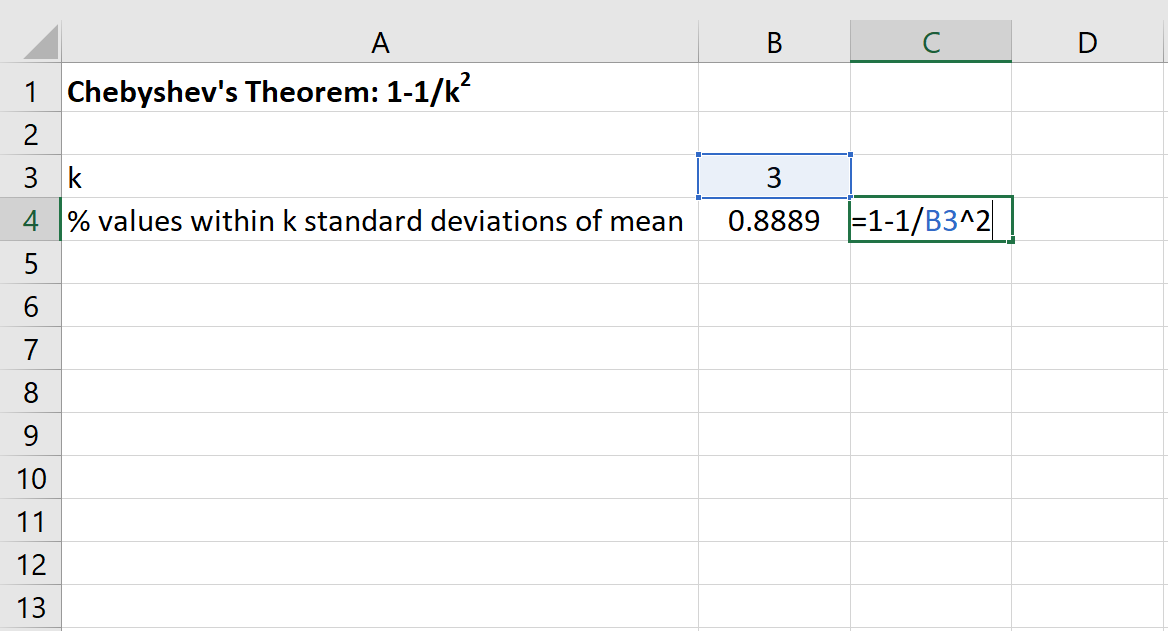
A porcentagem de valores entre 20 e 50 para este conjunto de dados será de pelo menos 88,89% .

Exemplo 3: Use o teorema de Chebyshev para determinar qual porcentagem de valores ficará entre 80 e 120 para um conjunto de dados com média de 100 e desvio padrão de 5.

Primeiro, determine o valor de k. Podemos fazer isso determinando quantos desvios padrão estão entre 80 e 120 da média:

(80 – média) / desvio padrão = (80 – 100) / 5 = -20/5 = -4

(120 – média) / desvio padrão = (120 – 100) / 5 = 20/5 = 4

Os valores 80 e 120 estão 4 desvios padrão abaixo e acima da média, respectivamente. Então, k = 4 .

Podemos então usar a seguinte fórmula no Excel para encontrar a porcentagem mínima de valores que estão dentro de 4 desvios padrão da média deste conjunto de dados:

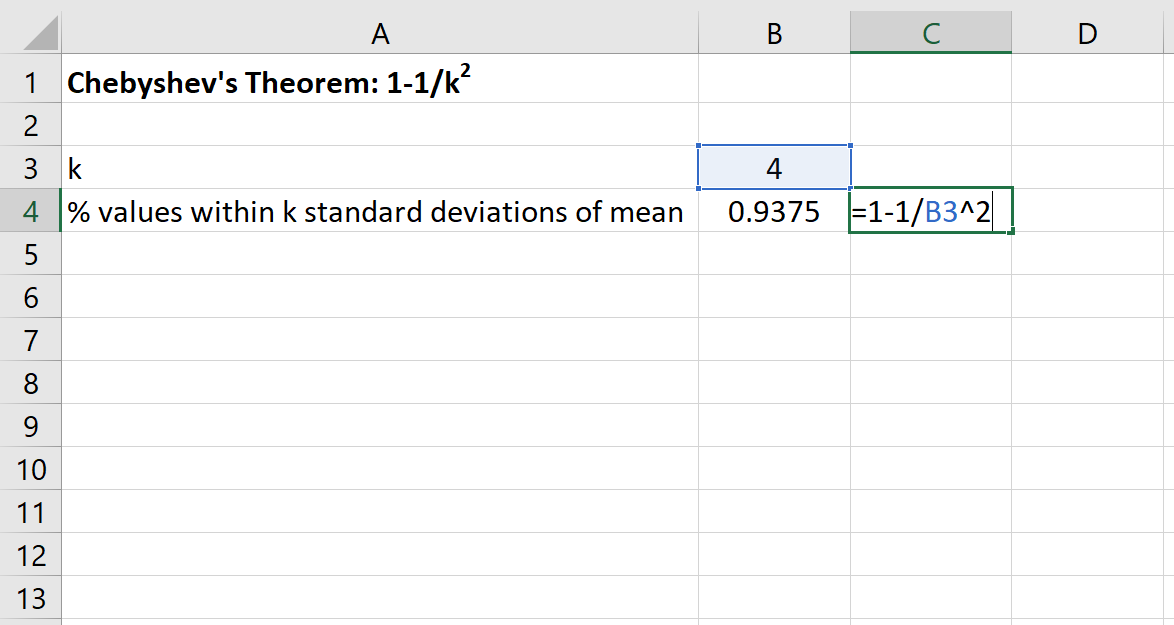
A porcentagem de valores entre 80 e 120 para este conjunto de dados será de pelo menos 93,75% .