Gráfico de caixa e bigode
Este artigo explica o que é um boxplot, também conhecido como box plot (ou boxplot). Você descobrirá como são feitos esses tipos de diagramas estatísticos e um exercício resolvido de um diagrama de caixa e bigode e sua interpretação.
O que é um gráfico de caixa e bigode?
O boxplot , também chamado de boxplot ou boxplot , é um gráfico que representa visualmente um conjunto de dados estatísticos por meio de quartis.
A principal característica do box and whisker plot é que ele permite visualizar rapidamente a dispersão de uma série de dados, pois indica os quartis, a mediana, os valores extremos e os outliers dos dados.
Assim, este tipo de diagrama é composto por uma caixa retangular e algumas linhas (ou bigodes) das quais emergem os seguintes valores:
- Os limites da caixa indicam o primeiro e terceiro quartis (Q 1 e Q 3 ). E a linha vertical dentro da caixa é a mediana (equivalente ao segundo quartil Q2 ).
- Os limites dos bigodes (ou braços) são os valores extremos , ou seja, o valor mínimo e o valor máximo da série de dados.
- Os pontos fora dos bigodes são outliers , ou seja, dados que provavelmente foram medidos incorretamente e, portanto, não devem ser levados em consideração no estudo estatístico.
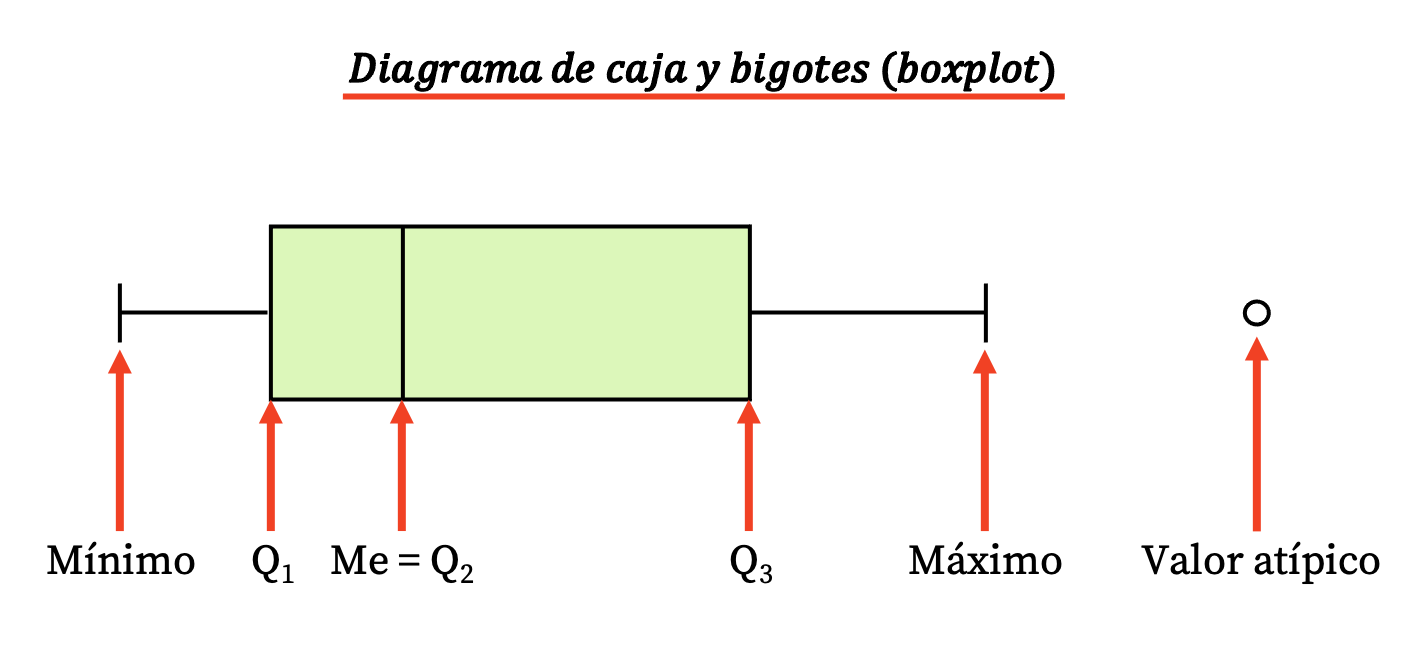
Observe que a diferença entre o terceiro e o primeiro quartil é o intervalo interquartil (ou intervalo interquartil), outra medida de dispersão estatística.
Os gráficos de caixa e bigode são muito úteis para comparar variáveis numéricas. No entanto, não é adequado para representar variáveis categóricas.
Como criar um gráfico de caixa e bigode
Para criar um box and whisker plot (ou boxplot) a partir de uma série de dados, as seguintes etapas devem ser executadas:
- Classifique os exemplos de dados estatísticos.
- Calcule os quartis (Q 1 , Q 2 e Q 3 ) e represente-os como a caixa no diagrama. O primeiro e o terceiro quartis correspondem aos limites da caixa, e para representar a mediana (o segundo quartil) deve-se traçar uma linha dentro da caixa onde está localizado o seu valor.
- Calcule o intervalo interquartil, que é igual ao terceiro quartil menos o primeiro quartil.
- Calcule os valores admissíveis LI e LS, cujas fórmulas são:
- Identifique valores discrepantes da amostra, que são valores menores que LI ou maiores que LS. Represente esses valores fora da faixa de bigodes com pontos.
- Identifique e represente os valores extremos, que são o menor valor e o maior valor no intervalo formado por LI e LS. Esses valores representam o final dos dois bigodes no diagrama.
![]()
![]()
![]()
Exemplo de gráfico de caixa e bigode
Considerando a definição e teoria do box and whisker plot (ou boxplot), você encontrará a seguir um exemplo concreto para entender melhor o conceito e ver como esse tipo de gráfico estatístico é realizado.
- Desenhe um boxplot do seguinte conjunto de dados estatísticos.

Neste caso, os dados já estão ordenados do menor para o maior, portanto nenhuma alteração é necessária. Caso contrário, devemos classificar os dados da amostra primeiro.
Em segundo lugar, extraímos os quartis da amostra:
![]()
![]()
![]()
Depois de calcularmos os três quartis, encontramos o intervalo interquartil subtraindo o quartil 3 menos o quartil 1:
![]()
Calculamos agora os limites LI e LS, que são os valores a partir dos quais os dados são considerados atípicos. Para fazer isso, você deve usar as seguintes fórmulas:
![]()
![]()
Portanto, neste caso temos dois valores discrepantes, porque 3,02 é menor que 3,16 e 5,71 é maior que 5,56.
![]()
Por fim, resta identificar os valores extremos, que são o mínimo e o máximo de todos os dados que estão no intervalo [LI,LS]. Portanto, no nosso exemplo, o valor mínimo é 3,70 e o valor máximo é 4,81.
![]()
![]()
Assim, uma vez identificados todos os valores da caixa e do bigode, resta fazer a representação gráfica:
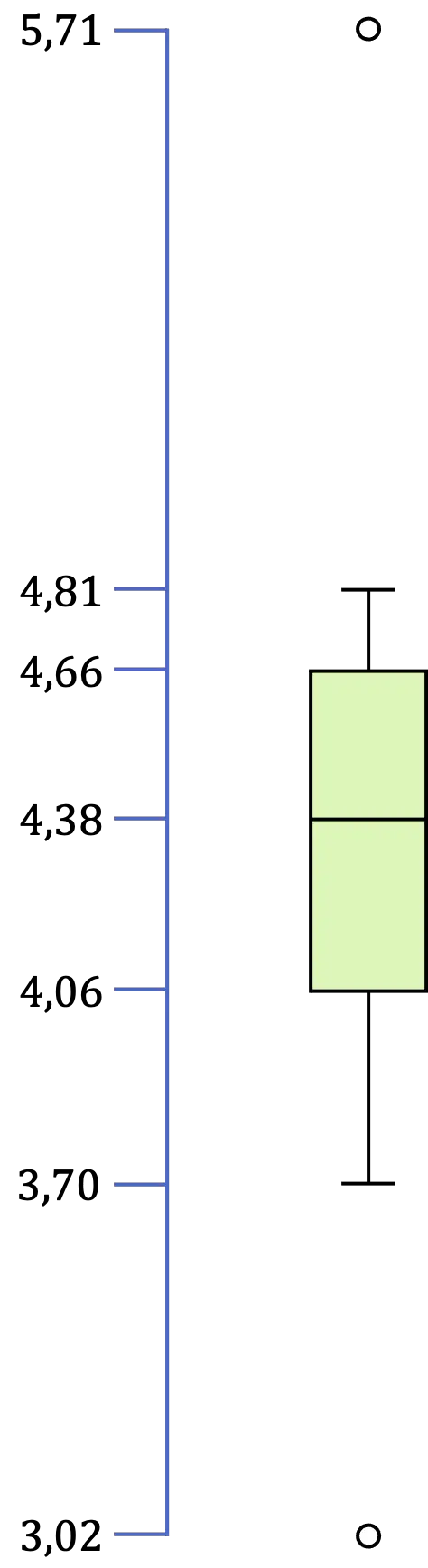
Para que serve um gráfico de caixa e bigode?
Por fim, vamos ver para que serve e como interpretar o box and whisker plot (ou boxplot).
Obviamente, o box and whisker plot é muito útil para conhecer rapidamente os quartis, intervalo interquartil, mediana, valores extremos e outliers de uma série de dados, já que todas essas medidas estatísticas podem ser identificadas com uma simples visualização.
Além disso, o box and whisker plot é utilizado para analisar a simetria da amostra estatística, pois representa visualmente todo o conjunto de dados. Se a mediana não estiver no centro da caixa, significa que a amostra não é simétrica.
Da mesma forma, os boxplots são muito utilizados no mercado de ações para representar a variação do preço de uma ação ao longo de um período de tempo, pois permitem visualizar o valor máximo, o valor mínimo e os valores intermediários em um curto período de tempo. tempo e assim tomar decisões mais rápidas.