Comparação de pontuações z de diferentes distribuições

Uma pontuação z informa quantos desvios padrão um valor de dados individual cai da média. É calculado da seguinte forma:

pontuação z = (x – μ) / σ

Ouro:

• x: valor de dados individuais
• μ: média populacional
• σ: desvio padrão populacional

Uma pontuação z para um valor individual pode ser interpretada da seguinte forma:

• Escore z positivo: o valor individual está acima da média.
• Escore z negativo: o valor individual é inferior à média.
• Uma pontuação z de 0: o valor individual é igual à média.

As pontuações Z são particularmente úteis quando queremos comparar a posição relativa de dois pontos de dados de duas distribuições diferentes. Para ilustrar isso, considere o seguinte exemplo.

Exemplo: Comparando pontuações Z

As pontuações em um determinado exame universitário são normalmente distribuídas com média μ = 80 e desvio padrão σ = 4. Duane obteve 84 neste exame.

As notas em outro exame da faculdade são normalmente distribuídas com média μ = 85 e desvio padrão σ = 8. Debbie tira 90 nesse exame.

Em comparação com a sua própria distribuição de notas nos exames, quem obteve os melhores resultados no exame?

Para responder a esta pergunta, podemos calcular a pontuação z da nota do exame de cada pessoa:

Pontuação z de Duane = (x – μ) / σ = (84 – 80) / 4 = 4/4 = 1

Pontuação z de Debbie = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625

Debbie Embora tenha pontuado mais alto, a pontuação de Duane é na verdade mais alta em comparação com a distribuição de seu exame específico.

Para entender isso, ajuda visualizar a situação. Aqui está a pontuação de Duane em comparação com a análise específica do exame:

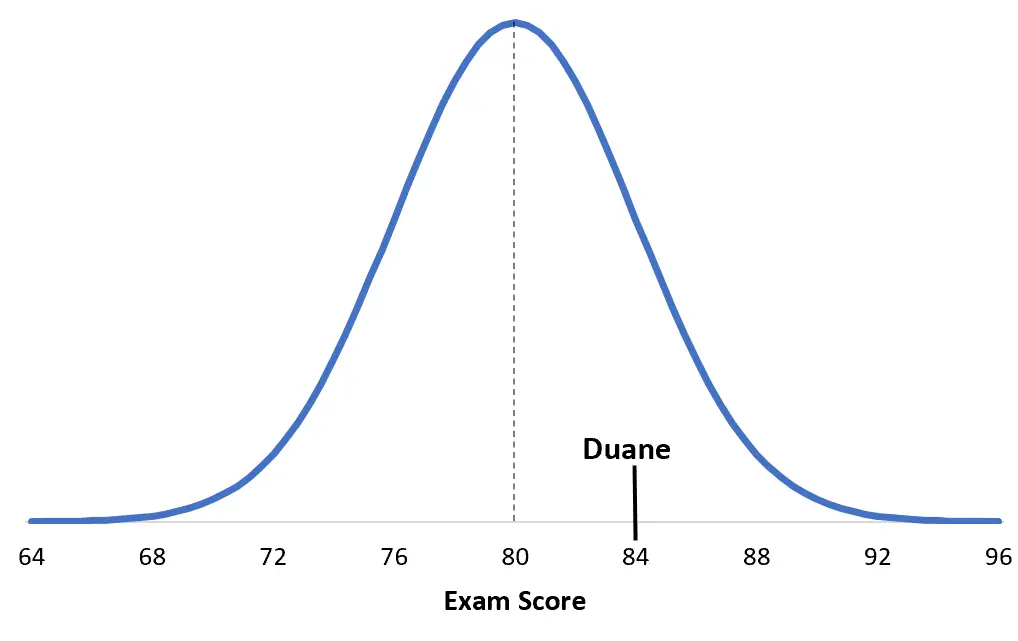
E aqui está a pontuação de Debbie no exame:

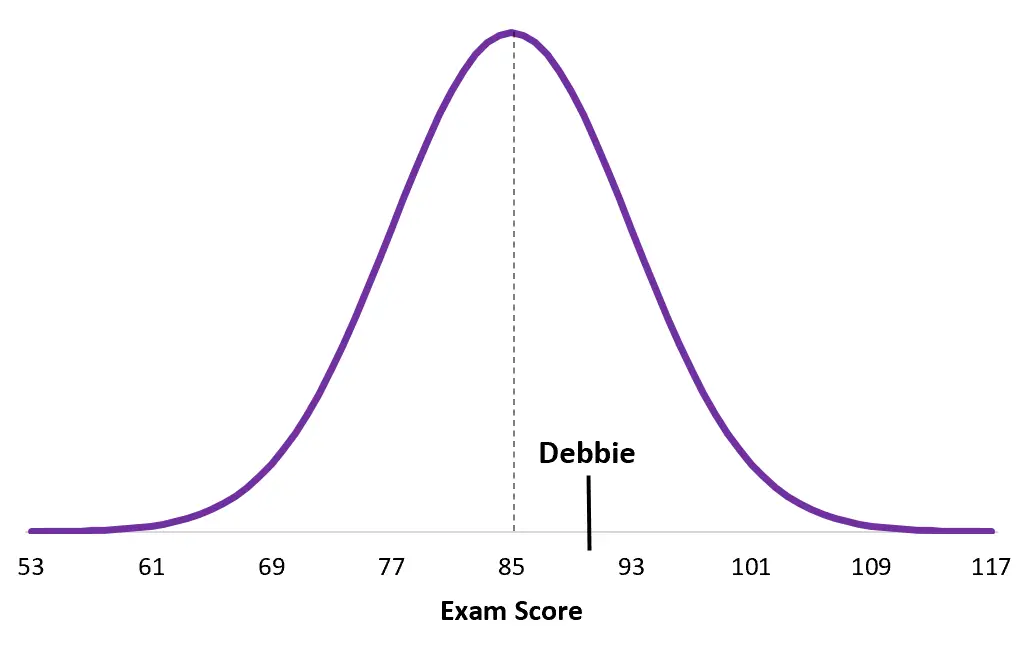
Observe como a pontuação de Debbie está muito mais próxima da média de sua população do que a de Duane. Embora ela tenha uma pontuação geral mais alta, sua pontuação z é mais baixa simplesmente porque a pontuação média em seu exame específico é mais alta.

Este exemplo ilustra por que as pontuações z são tão úteis para comparar valores de dados de diferentes distribuições: as pontuações z levam em consideração a média e os desvios padrão das distribuições, o que nos permite comparar valores de dados de diferentes distribuições e ver qual é maior em comparação com suas próprias distribuições.

Recursos adicionais

Calculadora de pontuação Z
Compare a calculadora de pontuação Z