Como ler a tabela de distribuição binomial

A tabela de distribuição binomial   é uma tabela que mostra as probabilidades associadas à distribuição binomial . Para usar a tabela de distribuição binomial, você só precisa de três valores:

• n: o número de tentativas
• r: o número de “sucessos” durante n tentativas
• p: a probabilidade de sucesso de uma determinada tentativa

Usando esses três números, você pode usar a tabela de distribuição binomial para encontrar a probabilidade de obter exatamente r sucessos ao longo de n tentativas, quando a probabilidade de sucesso em cada tentativa for p .

Os exemplos a seguir ilustram como ler a tabela de distribuição binomial.

Exemplo 1

Pergunta: Jéssica acerta 60% de suas tentativas de lance livre. Se ela acertar 6 lances livres, qual é a probabilidade de ela acertar exatamente 4?

Para responder a esta questão, podemos encontrar o valor na tabela de distribuição binomial que corresponde a n = 6, r = 4 e p = 0,60:

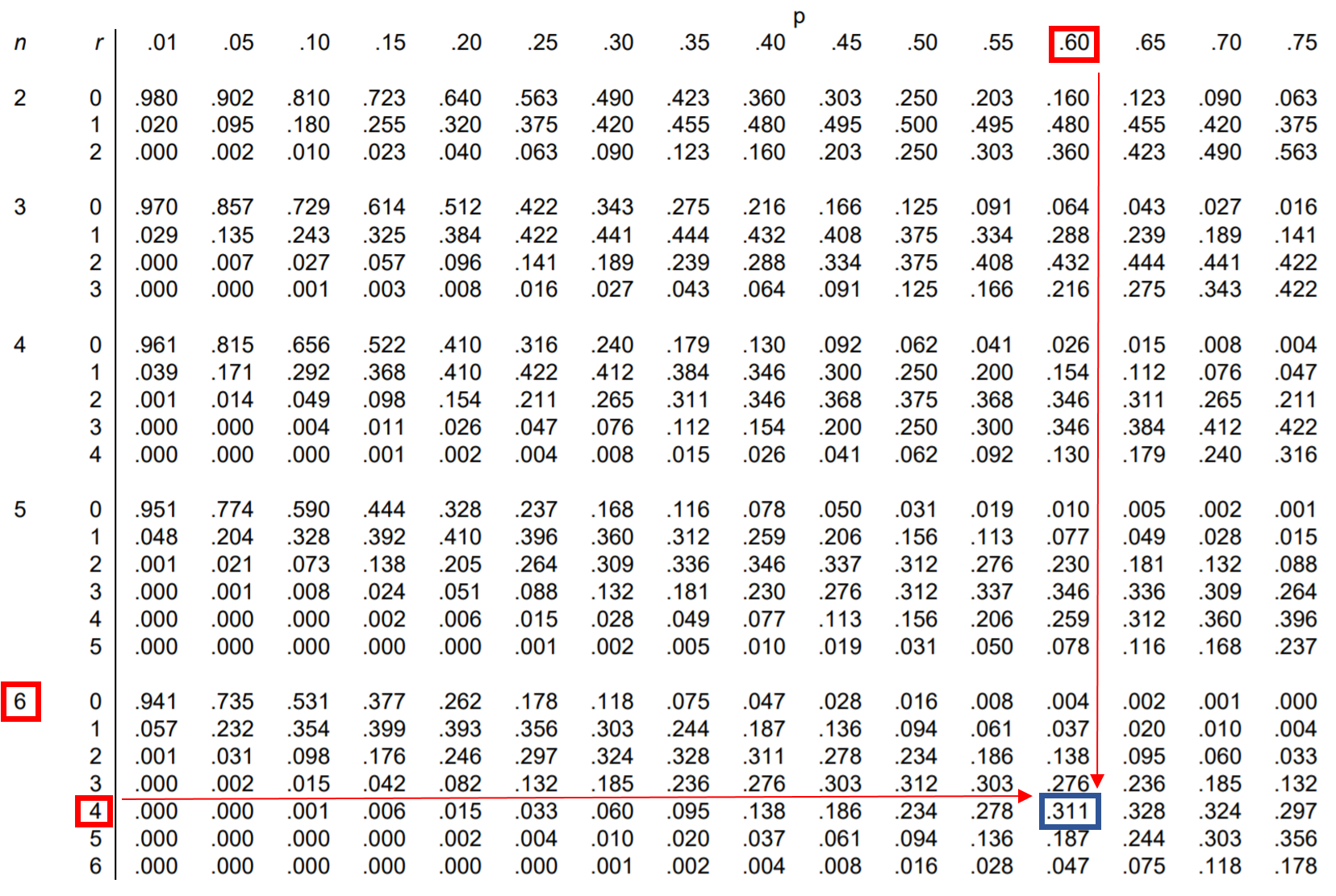
A probabilidade de Jéssica acertar exatamente 4 de 6 lances livres é 0,311 .

Exemplo 2

Pergunta: Jéssica acerta 60% de suas tentativas de lance livre. Se ela acertar 6 lances livres, qual é a probabilidade de ela acertar menos de 4?

Para encontrar essa probabilidade, você realmente precisa adicionar as seguintes probabilidades:

P(rende menos que 4) = P(rfaz 0) + P(rfaz 1) + P(rfaz 2) + P(rfaz 3)

Portanto, podemos procurar cada uma dessas quatro probabilidades na tabela de distribuição binomial e somá-las:

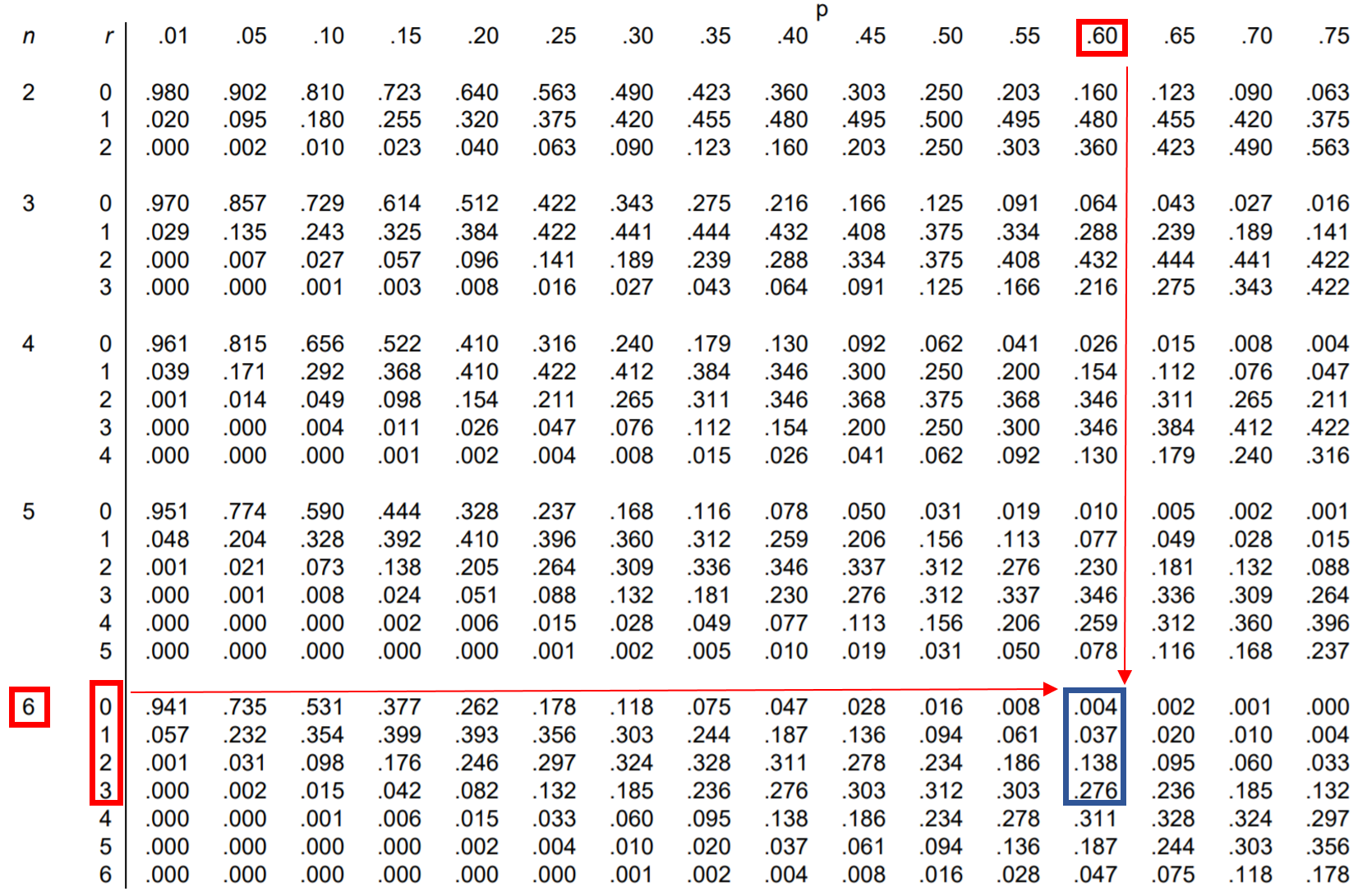
Na tabela, P(é menor que 4) = 0,004 + 0,037 + 0,138 + 0,276 = 0,455 .

A probabilidade de Jéssica acertar menos de 4 lances livres é de 0,455 .

Exemplo 3

Pergunta: Jéssica acerta 60% de suas tentativas de lance livre. Se ela acertar 6 lances livres, qual é a probabilidade de ela acertar 4 ou mais?

Para encontrar essa probabilidade, devemos adicionar as seguintes probabilidades:

P(faz 4 ou mais) = P(faz 4) + P(faz 5) + P(faz 6)

Portanto, podemos procurar cada uma dessas três probabilidades na tabela de distribuição binomial e somá-las:

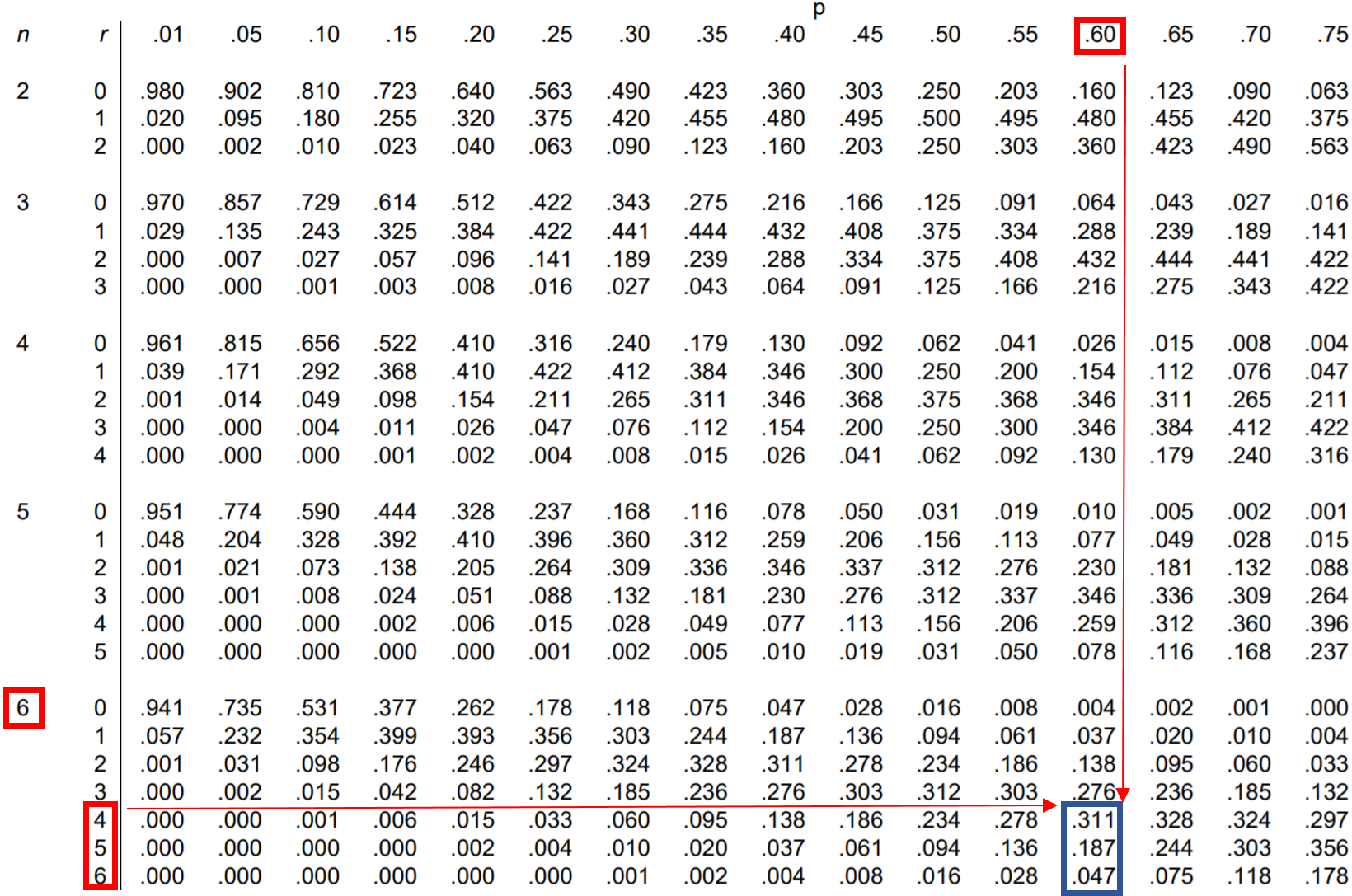
Da tabela, P(faz 4 ou mais) = 0,311 + 0,187 + 0,047 = 0,545 .

A probabilidade de Jéssica acertar 4 ou mais lances livres é 0,545 .