Diferença média
Este artigo explica o que é o desvio médio e como ele é calculado. Você também encontrará exemplos concretos de cálculo do desvio médio. E, além disso, você poderá calcular o desvio médio de qualquer conjunto de dados estatísticos usando uma calculadora online.
O que é desvio médio?
O desvio médio , também chamado de desvio médio absoluto , é uma medida de dispersão estatística.
O desvio médio de um conjunto de dados é a média dos desvios absolutos . Portanto, o desvio médio é igual à soma dos desvios de cada item de dados da média aritmética dividida pelo número total de itens de dados.
Em outras palavras, a fórmula do desvio médio é a seguinte:

👉 Você pode usar a calculadora abaixo para calcular o desvio médio de qualquer conjunto de dados.
Nas estatísticas, o desvio médio também é chamado de desvio médio absoluto .
A interpretação do desvio médio é feita da seguinte forma: quanto maior o valor do desvio médio, significa que os dados estão, em média, mais afastados da média aritmética; inversamente, quanto menor o desvio médio, mais próximo o valor. os dados são. O desvio médio indica, portanto, a dispersão de uma série de dados.
Outras medidas consideradas distribuídas são amplitude, intervalo interquartil, desvio padrão (ou desvio padrão), variância e coeficiente de variação.
Como calcular o desvio médio
Para calcular o desvio médio de uma série de dados, devem ser seguidos os seguintes passos:
- Calcule a média aritmética do conjunto de dados estatísticos.
- Calcule o desvio de cada ponto de dados da média, definido como o valor absoluto da diferença entre os dados e a média.
- Some todas as diferenças calculadas na etapa anterior.
- Divida pelo número total de dados. O resultado obtido é o desvio médio da série de dados.
Em resumo, a fórmula que deve ser aplicada para encontrar o desvio médio é:
![]()
Exemplo de cálculo do desvio médio
Considerando a definição de desvio médio, segue abaixo um exemplo resolvido passo a passo de cálculo do desvio médio de uma amostra estatística. Assim você entenderá melhor como obter o desvio médio.
- Um analista estuda os resultados econômicos de uma empresa no ano passado e tem informações sobre o lucro obtido pela empresa em cada trimestre desse ano: 2, 3, 7 e 5 milhões de dólares. Qual é o desvio médio dos dados?
Primeiro, precisamos calcular a média dos dados, então somamos e dividimos pelo número total de observações (4):
![]()
Depois de calcular a média aritmética, usamos a fórmula do desvio médio:
![]()
Substituímos os dados na fórmula:
![]()
Fazemos os cálculos no numerador:
![]()
![]()
![]()
E por fim, dividimos pelo número total de dados para obter o desvio médio da amostra:
![]()
Calculadora de desvio médio
Insira um conjunto de dados estatísticos na calculadora a seguir para calcular seu desvio médio. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.
Desvio médio para dados agrupados
Para calcular o desvio médio dos dados agrupados em intervalos, devem ser seguidos os seguintes passos:
- Determine a média aritmética do conjunto de dados estatísticos. Como os dados estão agrupados, a expressão para calcular a média é:
- Calcule o desvio de cada intervalo da média, que equivale ao valor absoluto da diferença entre a nota da turma e a média.
- Multiplique o desvio de cada intervalo pela sua frequência absoluta.
- Some todos os resultados da etapa anterior e divida pelo número total de dados. O resultado obtido é o desvio médio da amostra agrupada em intervalos.
![]()
![]()
![]()
![]()
Concluindo, a fórmula para obter o desvio médio dos dados agrupados é:
![]()
Quando os dados são agrupados, geralmente significa que há muitos dados e encontrar o desvio médio envolve muitas etapas. Portanto, geralmente são utilizadas tabelas de frequência para realizar o cálculo.
Abaixo está um exercício passo a passo sobre como calcular o desvio médio quando os dados são agrupados em intervalos:
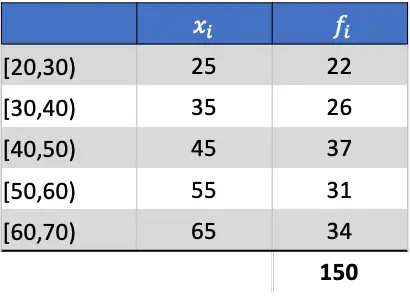
A primeira coisa a fazer é calcular a média dos dados agrupados. Para fazer isso, adicionamos uma coluna à tabela multiplicando a nota da turma pela sua frequência:
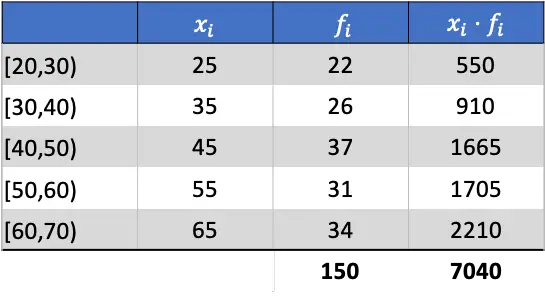
A média aritmética será, portanto, o resultado da divisão da soma da coluna somada pela soma das frequências absolutas:
![]()
Agora que sabemos a média dos dados, podemos adicionar todas as colunas necessárias para encontrar o desvio médio:
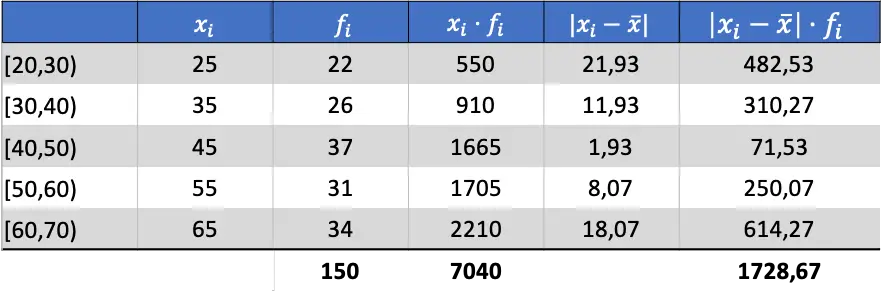
Assim, para obter o desvio médio deve-se dividir a soma da última coluna pelo número total de observações:
![]()