Uma introdução à distribuição multinomial
A distribuição multinomial descreve a probabilidade de obter um número específico de contagens para k resultados diferentes, quando cada resultado tem uma probabilidade fixa de ocorrer.
Se uma variável aleatória _ puder ser encontrada pela seguinte fórmula:
Probabilidade = n! * (p 1 x 1 * p 2 x 2 * … * p k x k ) / (x 1 ! * x 2 ! … * x k !)
Ouro:
- n: número total de eventos
- x 1 : número de vezes que o resultado 1 ocorre
- p 1 : probabilidade de que o resultado 1 ocorra em uma determinada tentativa
Por exemplo, suponha que haja 5 bolinhas vermelhas, 3 bolinhas verdes e 2 bolinhas azuis em uma urna. Se retirarmos aleatoriamente 5 bolinhas de gude da urna, com reposição, qual é a probabilidade de obter exatamente 2 bolinhas vermelhas, 2 bolinhas verdes e 1 bolinha azul?
Para responder a esta questão, podemos usar a distribuição multinomial com os seguintes parâmetros:
- número : 5
- x 1 (# bolinhas de gude vermelhas) = 2, x 2 (# bolinhas de gude verdes) = 2, x 3 (# bolinhas de gude azuis) = 1
- p 1 (prob. vermelho) = 0,5, p 2 (prob. verde) = 0,3, p 3 (prob. azul) = 0,2
Colocando esses números na fórmula, descobrimos que a probabilidade é:
Probabilidade = 5! * (0,5 2 * 0,3 2 * 0,2 1 ) / (2! * 2! * 1!) = 0,135 .
Problemas práticos de distribuição multinomial
Use os seguintes problemas práticos para testar seu conhecimento sobre distribuição multinomial.
Nota: Usaremos a Calculadora de Distribuição Multinomial para calcular as respostas a essas perguntas.
Problema 1
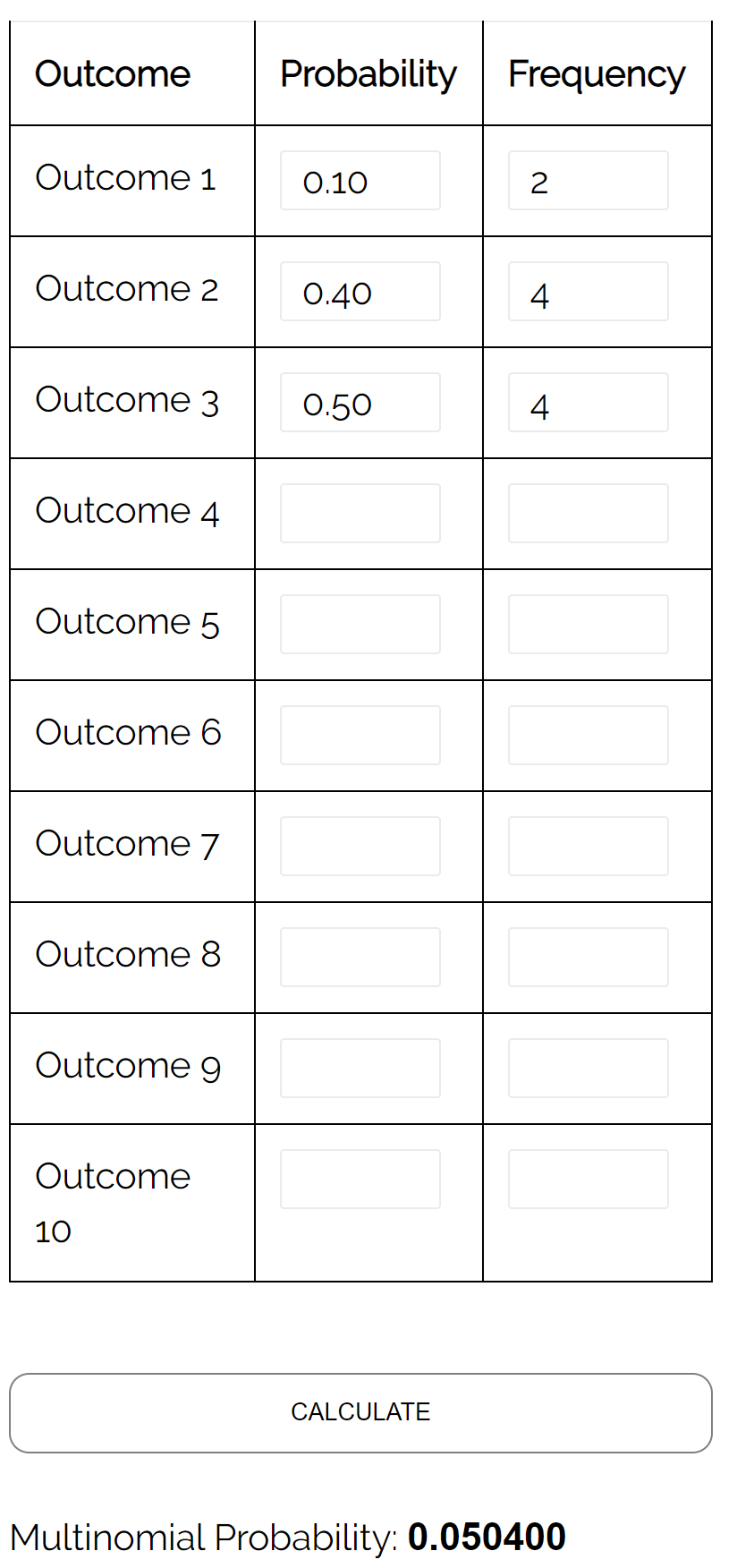
Pergunta: Em uma eleição tripartida para prefeito, o candidato A recebe 10% dos votos, o candidato B recebe 40% dos votos e o candidato C recebe 50% dos votos. Se selecionarmos uma amostra aleatória de 10 eleitores, qual é a probabilidade de que 2 tenham votado no candidato A, 4 votassem no candidato B e 4 votassem no candidato C?
Resposta: Usando a Calculadora de Distribuição Multinomial com as seguintes entradas, descobrimos que a probabilidade é 0,0504:
Problema 2
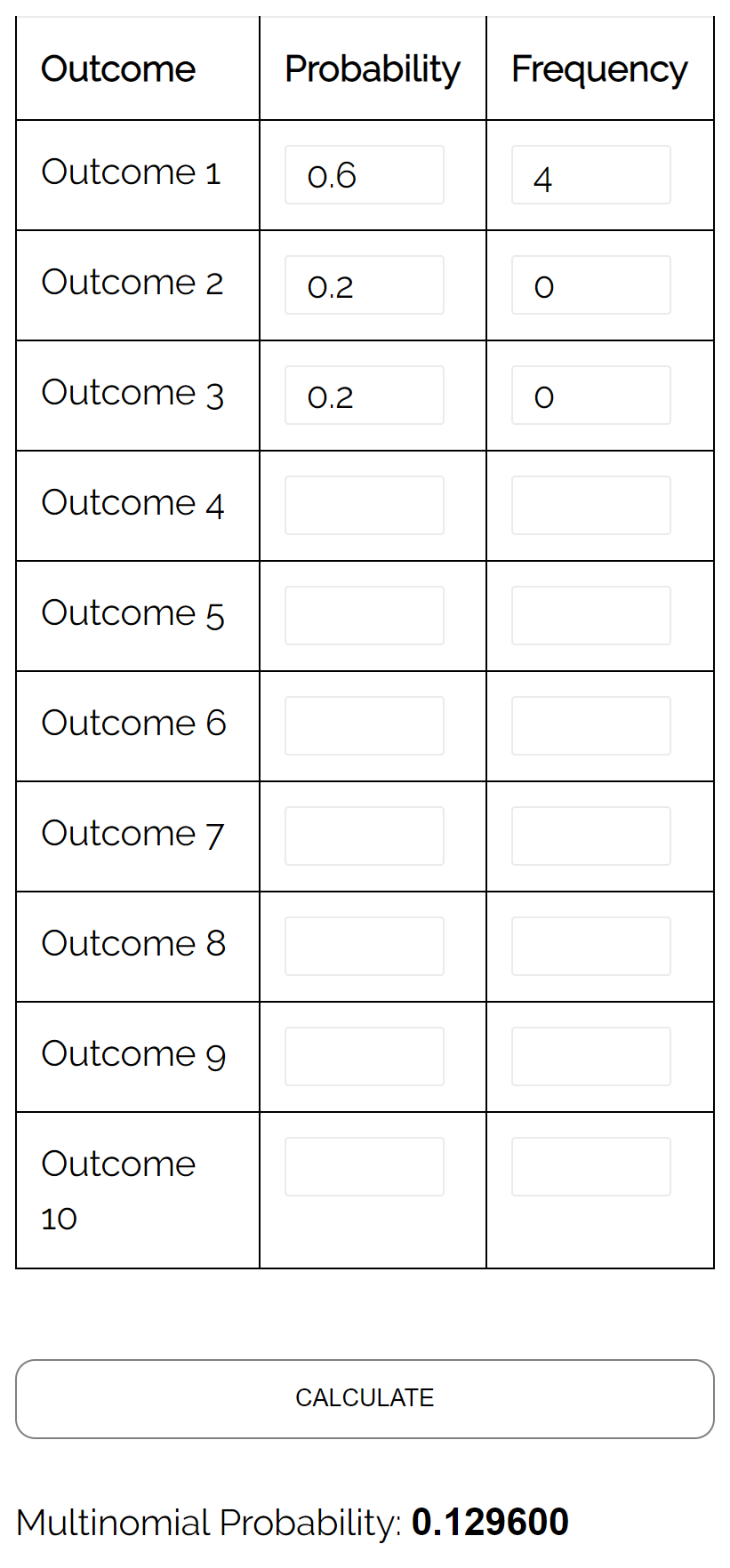
Pergunta: Suponha que uma urna contenha 6 bolinhas amarelas, 2 bolinhas vermelhas e 2 bolinhas rosa. Se selecionarmos aleatoriamente 4 bolas da urna, com reposição, qual é a probabilidade de todas as 4 bolas serem amarelas?
Resposta: Usando a Calculadora de Distribuição Multinomial com as seguintes entradas, descobrimos que a probabilidade é 0,1296:
Problema 3
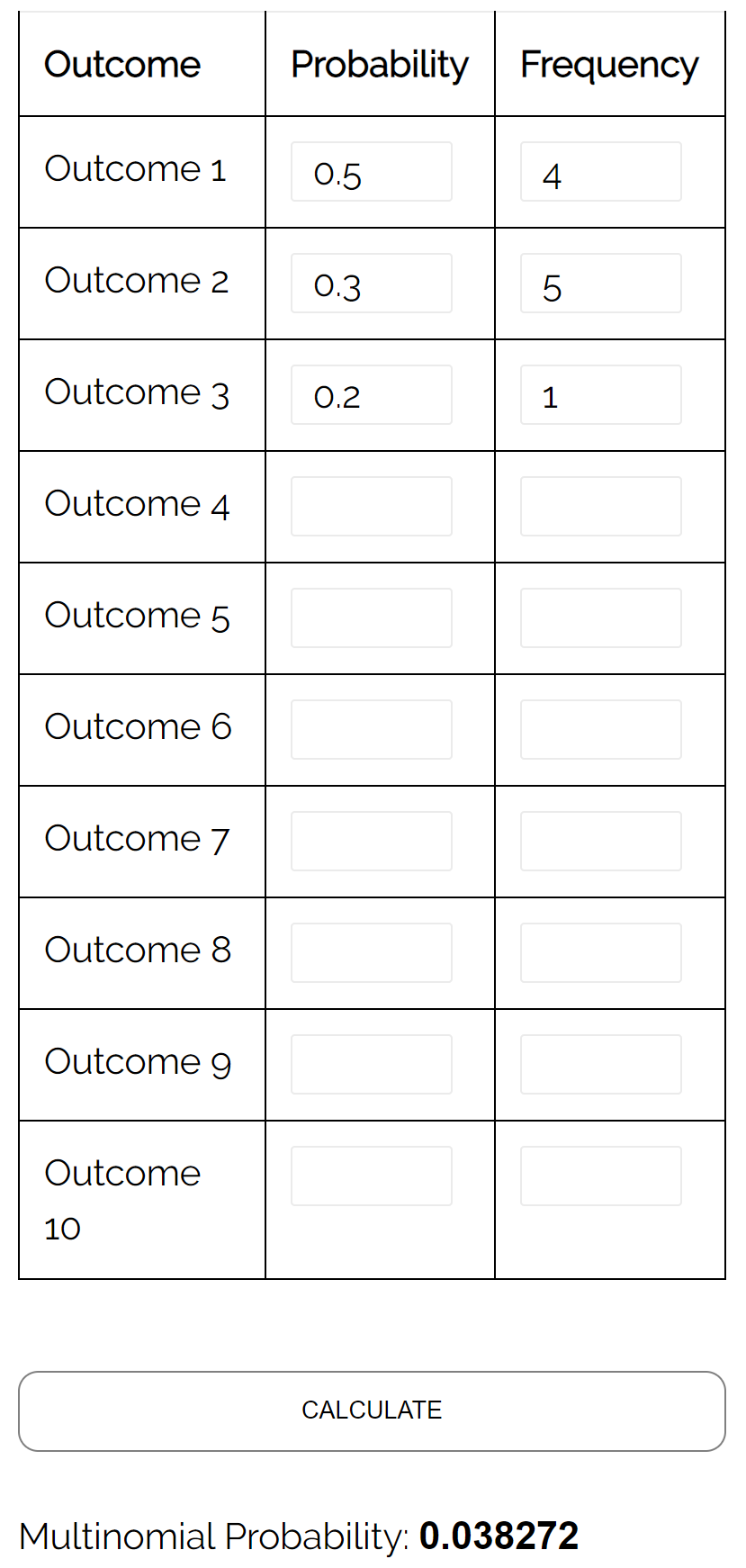
Pergunta: Suponha que dois alunos estejam jogando xadrez um contra o outro. A probabilidade de o aluno A vencer um determinado jogo é 0,5, a probabilidade de o aluno B vencer um determinado jogo é 0,3 e a probabilidade de haver empate em um determinado jogo é 0, 2. Se eles jogarem 10 jogos, qual é o probabilidade de que o jogador A ganhe 4 vezes, o jogador B ganhe 5 vezes e empatem 1 vez?
Resposta: Usando a Calculadora de Distribuição Multinomial com as seguintes entradas, descobrimos que a probabilidade é 0,038272:
Recursos adicionais
Os tutoriais a seguir fornecem uma introdução a outras distribuições comuns em estatísticas:
Uma introdução à distribuição normal
Uma introdução à distribuição binomial
Uma introdução à distribuição de Poisson
Uma introdução à distribuição geométrica