Como realizar manualmente uma anova de medidas repetidas
Uma ANOVA de medidas repetidas é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos em que os mesmos sujeitos aparecem em cada grupo.
Este tutorial explica como realizar manualmente uma ANOVA de medidas repetidas unilaterais.
Exemplo: ANOVA de medidas repetidas unidirecionais manualmente
Os pesquisadores querem saber se três medicamentos diferentes causam tempos de reação diferentes. Para testar isso, eles medem o tempo de reação (em segundos) de cinco pacientes a cada medicamento. Os resultados são mostrados abaixo:
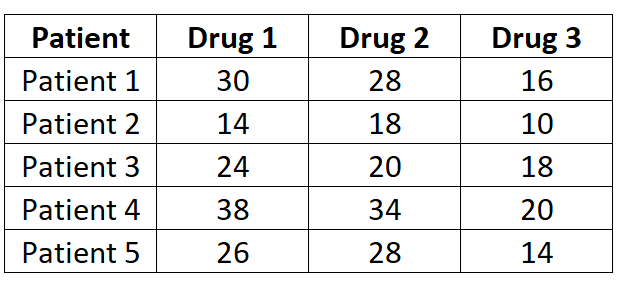
Como cada paciente é medido com cada um dos três medicamentos, usaremos uma ANOVA de medidas repetidas unilaterais para determinar se o tempo médio de reação difere entre os medicamentos.
Siga as etapas a seguir para realizar manualmente a ANOVA de medidas repetidas:
Etapa 1: Calcule o SST.
Primeiro, calcularemos a soma total dos quadrados (SST), que pode ser encontrada usando a seguinte fórmula:
SST = s 2 total (n total -1)
Ouro:
- s 2 total : a variação do conjunto de dados
- n total : o número total de observações no conjunto de dados
Neste exemplo, calculamos a TSM da seguinte forma: (64,2667)(15-1) = 899,7
Passo 2: Calcular SSB
A seguir, calcularemos a soma dos quadrados (SSB), que pode ser encontrada usando a seguinte fórmula:
SSB = Σn j ( x j – x total ) 2
Ouro:
- Σ : um símbolo grego que significa “soma”
- n j : o número total de observações no j- ésimo grupo
- x j : a média do j-ésimo grupo
- x total : a média de todos os dados
Neste exemplo, calculamos SSB da seguinte forma: (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Etapa 3: Calcule o SSS.
A seguir, calcularemos a soma dos quadrados temática (SSS), que pode ser encontrada usando a seguinte fórmula:
SSS =(Σr 2 k /c) – (N 2 /rc)
Ouro:
- Σ : um símbolo grego que significa “soma”
- r 2 k : soma quadrada do k-ésimo paciente
- N: o total geral de todos os dados
- r: número total de pacientes
- c: número total de grupos
Neste exemplo, calculamos SSS da seguinte forma: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1
Etapa 4: Calcule o SES.
A seguir, calcularemos a soma do erro quadrático (SSE), que pode ser encontrada usando a seguinte fórmula:
SSE = SST – SSB – SSS
Neste exemplo, calculamos o SES da seguinte forma: 899,7 – 362,1 – 441,1 = 96,5
Etapa 5: Preencha a tabela ANOVA de medidas repetidas.
Agora que temos SSB, SSS e SSE, podemos preencher a tabela ANOVA de medidas repetidas:
| Fonte | Soma dos quadrados (SS) | df | Quadrados médios (MS) | F |
|---|---|---|---|---|
| Entre | 362,1 | 2 | 181,1 | 15.006 |
| Assunto | 441,1 | 4 | 110,3 | |
| Erro | 96,5 | 8 | 12.1 |
Aqui está como calculamos os diferentes números na tabela:
- df entre: #grupos – 1 = 3 – 1 = 2
- assunto df: #participantes – 1 = 5 – 1 = 4
- Erro df: df entre * df sujeito = 2*4 = 8
- MS entra: SSB / df entra = 362,1 / 2 = 181,1
- Disciplina MS: disciplina SSS / df = 441,1 / 4 = 110,3
- Erro MS: erro SSE / df = 96,5 / 8 = 12,1
- F: MS entra / erro MS = 181,1 / 12,1 = 15,006
Etapa 6: interprete os resultados.
A estatística do teste F para esta ANOVA de medidas repetidas unilaterais é 15,006 . Para determinar se este é um resultado estatisticamente significativo, precisamos compará-lo com o valor crítico de F encontrado na tabela de distribuição F com os seguintes valores:
- α (nível de significância) = 0,05
- DF1 (graus de liberdade do numerador) = df entre = 2
- DF2 (graus de liberdade do denominador) = erro df = 8
Descobrimos que o valor crítico de F é 4,459 .
Como a estatística do teste F na tabela ANOVA é maior que o valor crítico F na tabela de distribuição F, rejeitamos a hipótese nula. Isto significa que temos evidências suficientes para afirmar que existe uma diferença estatisticamente significativa entre os tempos médios de resposta dos medicamentos.