Uma introdução à ancova (análise de variância)

ANCOVA significa “análise de covariância”. Para entender como funciona uma ANCOVA, é útil primeiro entender a ANOVA.

Uma ANOVA   (análise de variância) é usada para determinar se existe ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

Por exemplo, digamos que queremos saber se a técnica de estudo afeta ou não as notas dos exames de uma turma de alunos. Dividimos a turma em três grupos aleatoriamente. Cada grupo usa uma técnica de estudo diferente durante um mês para se preparar para um exame. No final do mês, todos os alunos fazem o mesmo exame.

Para saber se a técnica de estudo tem impacto nas notas dos exames, podemos realizar uma ANOVA unidirecional, que nos dirá se há diferença estatisticamente significativa entre as notas médias dos três grupos.

Uma ANCOVA é uma extensão de uma ANOVA na qual queremos determinar se existe uma diferença estatisticamente significativa entre três ou mais grupos independentes após contabilizar uma ou mais covariáveis .

Uma covariável é uma variável contínua que varia com a variável de resposta.

Por exemplo, digamos que queremos saber se a técnica de estudo tem ou não impacto nas notas dos exames, mas queremos levar em consideração a nota que o aluno já tem na aula . Podemos usar a nota atual como covariável e realizar uma ANCOVA para determinar se há uma diferença estatisticamente significativa entre as notas médias dos exames dos três grupos.

Isso nos permite testar se a técnica de estudo tem ou não impacto nas notas dos exames, uma vez removida a influência da covariável.

Assim, se constatarmos que existe uma diferença estatisticamente significativa nas notas dos exames entre as três técnicas de estudo, podemos ter certeza de que essa diferença existe mesmo depois de levar em conta a nota atual dos alunos na turma (c ‘ou seja, se eles já estão indo bem ou se já estão indo bem). não na aula) .

Suposições da ANCOVA

Antes de realizar uma ANCOVA, é importante garantir que as seguintes premissas sejam atendidas:

• A(s) covariável(es) e a(s) variável(is) de fator são independentes – A covariável e a variável de fator devem ser independentes uma da outra, porque adicionar um termo de covariável no modelo só faz sentido se a covariável e a variável de fator agirem de forma independente no variável de resposta.
• As covariáveis são dados contínuos. As covariáveis devem ser contínuas (ou seja, dados de intervalo ou razão).
• Homogeneidade das variâncias – As variâncias entre os grupos devem ser aproximadamente iguais.
• Independência – As observações em cada grupo devem ser independentes.
• Normalidade – Os dados devem ser distribuídos aproximadamente normalmente em cada grupo.
• Sem valores discrepantes extremos – Não deve haver valores discrepantes extremos em nenhum dos grupos que possam afetar significativamente os resultados da ANCOVA.

ANCOVA: exemplo

Uma professora quer saber se três técnicas de estudo diferentes impactam as notas dos exames, mas ela quer levar em consideração a nota atual que o aluno já tem na turma.

Será realizada uma ANCOVA utilizando as seguintes variáveis:

• Variável fatorial: estudo técnico
• Covariável: pontuação atual
• Variável de resposta: nota do exame

A tabela a seguir apresenta o conjunto de dados dos 15 alunos recrutados para participar do estudo:

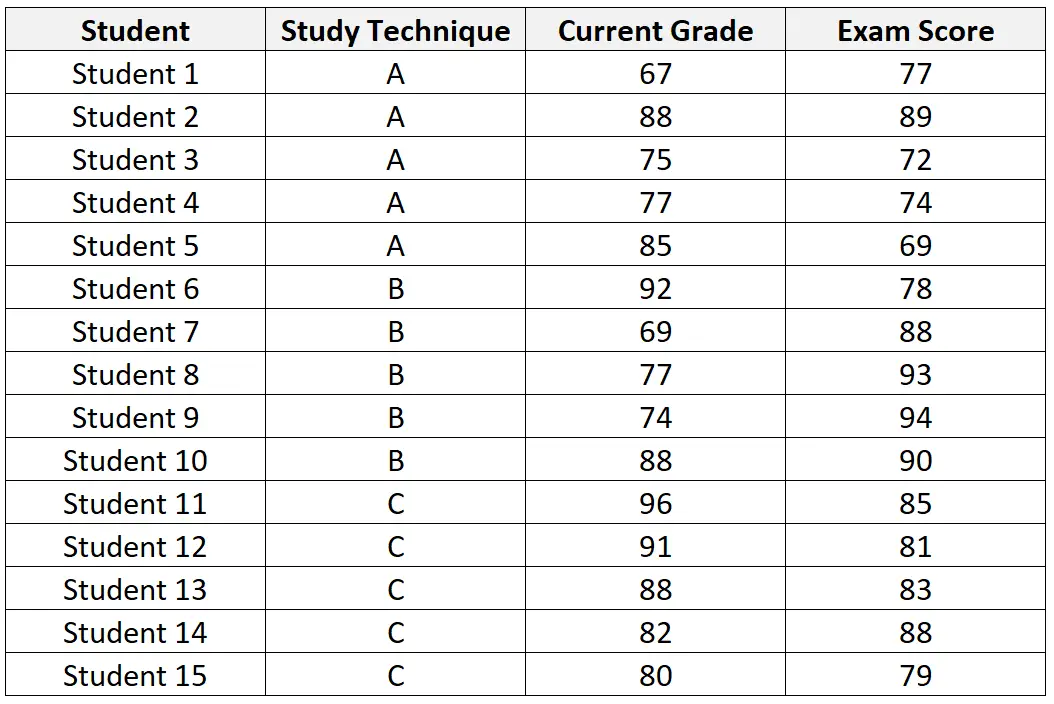
Após realizar uma ANCOVA no conjunto de dados, o professor obtém os seguintes resultados:

O valor p para a técnica de estudo é 0,03155 . Como este valor é inferior a 0,05, podemos rejeitar a hipótese nula de que cada uma das técnicas de estudo conduz à mesma nota média do exame, mesmo depois de contabilizada a nota atual do aluno na aula .

Para determinar exatamente quais técnicas de estudo produzem notas médias diferentes nos exames, o professor precisará realizar testes post-hoc .

Recursos adicionais

Como realizar uma ANCOVA no Excel
Como realizar uma ANCOVA em R
Como realizar uma ANCOVA em Python
As diferenças entre ANOVA, ANCOVA, MANOVA e MANCOVA